Bài 13 trang 72 SGK Toán 9 tập 2
Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Đề bài
Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Phương pháp giải - Xem chi tiết
+ Dựa vào tính chất tam giác cân và tính chất hai đường thẳng song song để chỉ ra các cung có số đo bằng nhau.
+ Sử dụng : “ Hai cung bằng nhau nếu chúng có số đo bằng nhau”
Lời giải chi tiết
TH1: Tâm đường tròn nằm trong hai dây song song
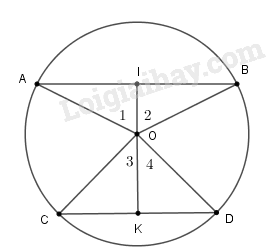
Giả sử \(AB\) và \(CD\) là các dây song song của đường tròn \((O)\). Ta chứng minh \(\overparen{AC}\)= \(\overparen{BD}\).
Kẻ \(OI \bot AB\) \((I \in AB)\) và \(OK \bot CD (K\in CD)\).
Do \(AB //CD\) nên \(OI \bot CD\) (Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia )
Do đó, OI trùng với OK (Qua O chỉ có 1 đường thẳng vuông góc với CD) hay \(I,O,K\) thẳng hàng.
Do các tam giác \(OAB, OCD\) là các tam giác cân đỉnh \(O\) nên các đường cao kẻ từ đỉnh đồng thời là phân giác.
Vì vậy ta có: \(\widehat {{O_1}} = \widehat {{O_2}} \) và \( \widehat {{O_3}} = \widehat {{O_4}}\)
Ta có: \(\widehat {AOC} = {180^0} - \widehat {{O_1}} - \widehat {{O_3}} = {180^0} - \widehat {{O_2}} - \widehat {{O_4}} = \widehat {BOD}\)
Suy ra \(\overparen{AC}\)= \(\overparen{BD}\).
TH2: Tâm đường tròn nằm ngoài hai dây song song
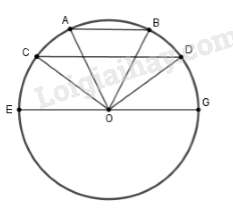
Giả sử đường tròn \(\left( O \right)\) có hai dây song song \(AB//CD.\) Ta chứng minh cung \(\overparen{AC}\) = \(\overparen{BD}\) .
Qua \(O\) kẻ đường kính \(EG//CD \Rightarrow EG//AB\) .
Nối \(OA,OC,OB,OD \Rightarrow OA = OB = OC = OD\) (= bán kính)
+ Xét tam giác \(OAB\) cân tại \(O\left( {{\rm{do}}\,OA = OB} \right)\) nên \(\widehat {OAB} = \widehat {OBA}\) (1)
Lại có \(EG//AB \Rightarrow \) \(\widehat {OAB} = \widehat {AOE};\,\widehat {OBA} = \widehat {BOG}\) (so le trong) (2)
Từ (1) và (2) \(\Rightarrow \) \(\widehat {EOA} = \widehat {BOG}\) (*)
+ Xét tam giác \(OCD\) cân tại \(O\left( {{\rm{do}}\,OC = OD} \right)\) nên \(\widehat {OCD} = \widehat {ODC}\) (3)
Lại có \(EG//CD \Rightarrow \) \(\widehat {OCD} = \widehat {COE};\,\widehat {ODC} = \widehat {DOG}\) (so le trong) (4)
Từ (3) và (4) suy ra \(\widehat {EOC} = \widehat {DOG}\) (**)
Từ (*) và (**) suy ra \(\widehat {EOA} - \widehat {EOC} = \widehat {BOG} - \widehat {DOG} \Leftrightarrow \widehat {AOC} = \widehat {BOD} \) \( \Rightarrow \overparen{AC}\) \(=\overparen{BD}\) (đpcm)