Bài 14 trang 77 SGK Toán 9 tập 1
Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh...
Đề bài
Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn \(\alpha\) tùy ý, ta có:
a) \(\tan \alpha =\dfrac{\sin\alpha }{\cos \alpha};\) \(\cot \alpha =\dfrac{\cos \alpha }{\sin \alpha };\) \(\tan \alpha . \cot \alpha =1\);
b) \(\sin^{2} \alpha +\cos^{2} \alpha =1\)
Gợi ý: Sử dụng định lý Py-ta-go.
Phương pháp giải - Xem chi tiết
+) Áp dụng công thức tính tỉ số lượng giác của một góc nhọn:
\(\sin \alpha =\dfrac{cạnh\ đối}{cạnh\ huyền};\) \(\cos \alpha = \dfrac{cạnh\ kề}{cạnh\ huyền}\);
\(\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề};\) \(\cot \alpha =\dfrac{cạnh\ kề}{cạnh\ đối}.\)
+) Sử dụng định lí Pytago trong tam giác vuông: \(\Delta{ABC}\) vuông tại \(A\), khi đó:
\(BC^2=AB^2+AC^2\)
Lời giải chi tiết
Xét \(\Delta{ABC}\) vuông tại \(A\), có \(\widehat{ACB}=\alpha\).
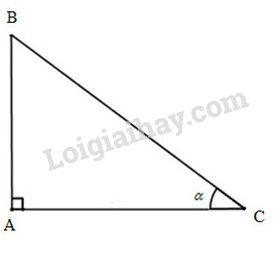
+) \(\Delta{ABC}\), vuông tại \(A\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
\(\sin \alpha = \dfrac{AB}{BC}\), \(\cos \alpha =\dfrac{AC}{BC}\)
\(\tan \alpha =\dfrac{AB}{AC}\), \(\cot \alpha =\dfrac{AC}{AB}\).
* Chứng minh \(\tan \alpha = \dfrac{\sin \alpha}{\cos \alpha}\).
\(VP=\dfrac{\sin \alpha}{\cos \alpha}=\dfrac{AB}{BC} : \dfrac{AC}{BC}=\dfrac{AB}{BC}.\dfrac{BC}{AC}=\dfrac{AB}{AC}= \tan \alpha =VT\)
(Trong đó VT là vế trái của đẳng thức; VP là vế phải của đẳng thức)
* Chứng minh \( \cot \alpha =\dfrac{\cos \alpha}{\sin \alpha}\).
\(VP=\dfrac{\cos \alpha}{\sin \alpha}=\dfrac{AC}{BC} : \dfrac{AB}{BC}=\dfrac{AC}{BC}. \dfrac{BC}{AB}=\dfrac{AC}{AB}=\cot \alpha=VT\)
* Chứng minh \(\tan \alpha . \cot \alpha =1\).
Ta có: \(VT=\tan \alpha . \cot \alpha \)
\(= \dfrac{AB}{AC}.\dfrac{AC}{AB}=1=VP\)
b) \(\Delta{ABC}\) vuông tại \(A\), áp dụng định lí Pytago, ta được:
\(BC^2=AC^2+AB^2\) (1)
Xét \(\sin ^{2} \alpha +\cos^{2}\alpha \)
\(\;\;\;={\left(\dfrac{AB}{BC} \right)^2}+ {\left(\dfrac{AC}{BC} \right)^2}= \dfrac{AB^{2}}{BC^{2}}+\dfrac{AC^{2}}{BC^{2}} = {{B{C^2}} \over {B{C^2}}} = 1 \)
Như vậy \(\sin^{2} \alpha +\cos^{2} \alpha =1\) (điều phải chứng minh)
Nhận xét: Ba hệ thức:
\(\tan \alpha =\dfrac{\sin \alpha }{\cos \alpha }\); \(\cot \alpha =\dfrac{\cos \alpha }{\sin \alpha }\) và \(\sin^{2} \alpha +\cos^{2} \alpha =1\) là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.