Đề kiểm tra 15 phút - Đề số 4 - Bài 5 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 5 - Chương 3 - Hình học 9
Đề bài
Cho đường tròn (O) đường kính AB. Một điểm C trên cung AB. Lấy trên dây AC một điểm D. Vẽ \(DE \bot AB\) tại E cắt đường tròn (O) tại P, Q ( D nằm giữa E và P ). Tiếp tuyến tai C của đường tròn cắt ED tại F. Chứng minh \(∆CDF\) cân.
Phương pháp giải - Xem chi tiết
Sử dụng:
+ G óc giữa tiếp tuyến và dây cung
+ Số đo góc có đỉnh bên trong đường tròn
Lời giải chi tiết
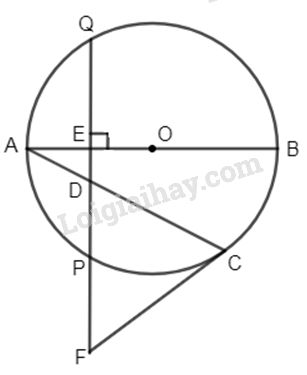
Gọi giao điểm của DE với đường tròn là P, Q.
Ta có : \(\widehat {DCF} = \dfrac{{sd\overparen{APC}} }{ 2} = \dfrac{{sd\overparen{AP} + sd\overparen{PC}}}{2}\) ( góc giữa tiếp tuyến và dây cung)
\(\widehat {CDF} = \dfrac{{sd\overparen{AQ }+ sd\overparen{PC}} }{ 2}\) ( góc có đỉnh bên trong đường tròn)
Mà \(\overparen{AP}=\overparen{ AQ}\) ( vì \(AB \bot PQ\))
Suy ra \(\widehat {CDF} = \widehat {DCF}\) hay \(∆CDF\) cân.