Đề kiểm tra 15 phút - Đề số 5 - Bài 3 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 3 - Chương 2 - Hình học 9
Đề bài
Cho điểm P nằm ngoài đường tròn (O; R) và \(OP = 2R.\) Một đường thẳng qua P cắt (O) tại A và B ( A nằm giữa B và P) và \(AB = R.\) Gọi H là chân đường vuông góc kẻ từ O đến PB.
a. Tính OH, AP theo R.
b. Kẻ một đường thẳng khác qua P cắt (O) tại C và D (CD ở khác phía với AB so với OP), kẻ \(OK ⊥ CD.\)
So sánh AB và CD biết \(OK < {{R\sqrt 3 } \over 2}\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
- Định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương các cạnh góc vuông
- Trong hai dây của một đường tròn:
+) Dây nào lớn hơn thì dây đó gần tâm hơn.
+) Dây nào gần tâm hơn thì dây đó lớn hơn.
Lời giải chi tiết
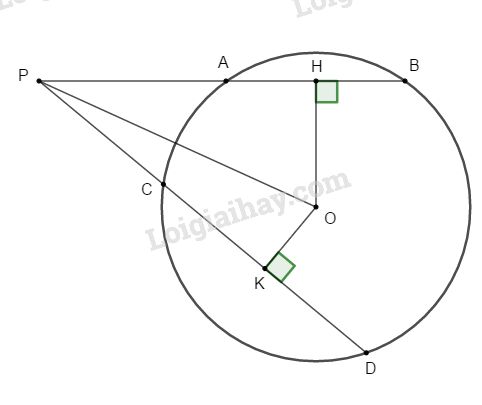
a. Ta có: \(OH ⊥ AB\) (gt)
\( \Rightarrow HA = HB = {{AB} \over 2} = {R \over 2}\)
(định lí đường kính dây cung)
Xét tam giác vuông AHO, ta có:
\(OH = \sqrt {A{O^2} - A{H^2}} \)\(\;= \sqrt {{R^2} - {{\left( {{R \over 2}} \right)}^2}} = {{R\sqrt 3 } \over 2}\)
∆PHO vuông tại H, ta có:
\(\eqalign{ & PH = \sqrt {P{O^2} - O{H^2}} \cr& = \sqrt {{{\left( {2R} \right)}^2} - {{\left( {{{R\sqrt 3 } \over 2}} \right)}^2}} = {{R\sqrt {13} } \over 2} \cr & \Rightarrow PA = PH - AH \cr&= {{R\sqrt {13} } \over 2} - {R \over 2} = {{R\left( {\sqrt {13} - 1} \right)} \over 2} \cr} \)
b. \(OK < {{R\sqrt 3 } \over 2}\) hay \(OK < OH = {{R\sqrt 3 } \over 2}\,\left( {cmt} \right)\)
\(\Rightarrow AB < CD\)