Đề kiểm tra 15 phút - Đề số 5 - Bài 4 - Chương 2 - Hình học 9 — Không quảng cáo

Đề bài

Cho ∆ABC có $AB = 6cm, AC = 8cm$ và $BC = 10cm$. Vẽ đường tròn (B; BA) và đường tròn (C; CA).

a. Chứng minh rằng AB là tiếp tuyến của đường tròn (C; CA) và AC là tiếp tuyến của đường tròn (B; BA).

b. AB cắt đường tròn (B) tại D và AC cắt đường tròn (C) tại E. Chứng minh rằng ba điểm D, M, E thẳng hàng (M là giao điểm thứ hai của hai đường tròn).

Lời giải chi tiết

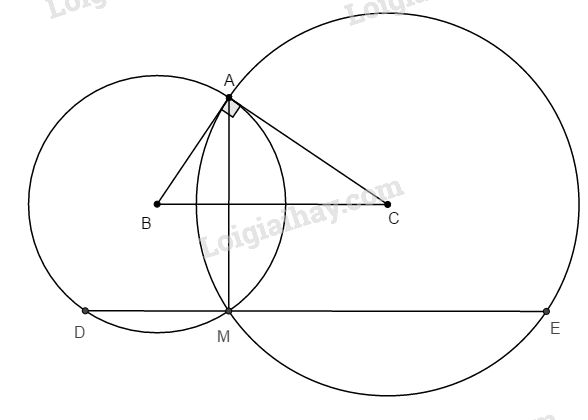
a. Ta có:

$\eqalign{  & A{B^2} + A{C^2} = B{C^2}  \cr  & \left( {{6^2} + {8^2} = {{10}^2}} \right) \cr}$

Theo định lí Pi-ta-go đảo ta có: ∆ABC vuông tại A hay $AB ⊥ AC ⇒$ AB là tiếp tuyến của (C; CA) và AC là tiếp tuyến của (B; BA).

b. Xét đường tròn tâm B có: $\widehat {AMD} = 90^\circ$ (AD là đường kính ) $⇒ MD ⊥ AM$ (1)

Xét đường tròn tâm C có $\widehat {AME} = 90^\circ$ (do AE là đường kính) $⇒ ME ⊥ AM$ (2)

Từ (1) và (2) suy ra MD và ME phải trùng nhau hay ba điểm D, M, E thẳng hàng.