Đề kiểm tra 15 phút - Đề số 5 - Bài 4 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 4 - Chương 1 - Hình học 9
Đề bài
Bài 1 . Tính \(A = {\cos ^2}55^\circ - \cot 58^\circ + {{\tan 52^\circ } \over {\cot 38^\circ }}\)\(\, + {\cos ^2}35^\circ + \tan 32^\circ \)
Bài 2 . Cho hình chữ nhật ABCD có đường chéo \(AC = 50cm\) và \(\widehat {BAC} = 30^\circ .\) Tính chu vi và diện tích hình chữ nhật.
LG bài 1
Phương pháp giải:
Sử dụng:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Lời giải chi tiết:
Ta có:
\({\cos ^2}35^\circ = {\sin ^2}55^\circ ;\cot 58^\circ = \tan 32^\circ ;\cot 38^\circ = \tan 52^\circ \)
Do đó:
\(\eqalign{ A &= {\cos ^2}55^\circ - \tan 32^\circ + {{\tan 52^\circ } \over {\tan 52^\circ }} + {\sin ^2}55^\circ + \tan 32^\circ \cr & = {\cos ^2}55^\circ + {\sin ^2}55^\circ + {{\tan 52^\circ } \over {\tan 52^\circ }} \cr&= 1 + 1 = 2 \cr} \)
LG bài 2
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
b) Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.
Lời giải chi tiết:
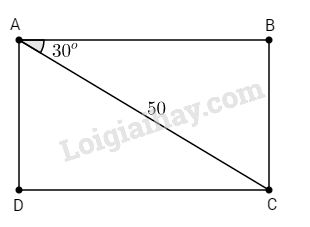
\(∆ABC\) vuông tại B có \(\widehat {BAC} = 30^\circ \) và \(AC = 50cm\) nên:
\(\eqalign{ & BC = AC.\sin 30^\circ \cr&\;\;\;\;\;\;\;= 50.\sin 30^\circ = 25\,\left( {cm} \right) \cr & AB = AC.\cos 30^\circ \cr&\;\;\;\;\;\;\; = 50.cos30^\circ = 25\sqrt 3 \,\left( {cm} \right) \cr} \)
Vậy chu vi hình chữ nhật ABCD là:
\(2(AB+BC) = 2\left( {25\sqrt 3 + 25} \right) \)
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= 50\left( {\sqrt 3 + 1} \right)\,\left( {cm} \right) \)
\( {S_{ABCD}} = AB.BC = 25\sqrt 3 .25 \)\(\;= 625\sqrt 3 \,\left( {c{m^2}} \right) \)