Đề kiểm tra 15 phút - Đề số 5 - Bài 4 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 4 - Chương 3 - Hình học 9
Đề bài
Cho góc nhọn AMB nội tiếp trong đường tròn (O). Trên nửa mặt phẳng bờ AB không chứa M, vẽ tia Ax sao cho \(\widehat {xAB} = \widehat {AMB}\). Chứng tỏ Ax là tiếp tuyến của (O).
Phương pháp giải - Xem chi tiết
Vẽ đường kính AC của (O), ta phải chứng minh Ax vuông góc AC
Lời giải chi tiết
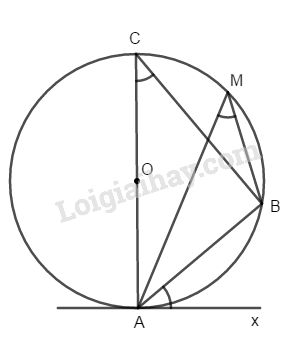
Vẽ đường kính AC của (O), ta phải chứng minh Ax vuông góc AC.
Thật vậy, ta có :
\(\widehat {ACB} = \widehat {AMB}\) (1)
( góc nội tiếp cùng chắn cung AB)
\(\widehat {AMB} = \widehat {xAB}\) (gt) (2)
mà \(\widehat {CBA} = 90^\circ \) ( AC là đường kính)
\(\Rightarrow \widehat {ACB} + \widehat {CAB} = 90^\circ \) (3)
Từ (1), (2) và (3) suy ra \(\widehat {CAB} + \widehat {xAB} = 90^\circ \)
Chứng tỏ Ax là tiếp tuyến của (O.
Xin các bạn lưu ý : Bài toán này là phần đảo của định lí về góc của tiếp tuyến và một dây, dùng để chứng minh.