Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 9 — Không quảng cáo

Đề bài

Từ điểm P nằm ngoài đường tròn (O; R), vẽ hai tiếp tuyến PA, PB (A, B là các tiếp điểm). Gọi H là chân đường vuông góc kẻ từ A đến đường kính BC. Chứng minh rằng PC cắt AH tại trung điểm I của AH.

Lời giải chi tiết

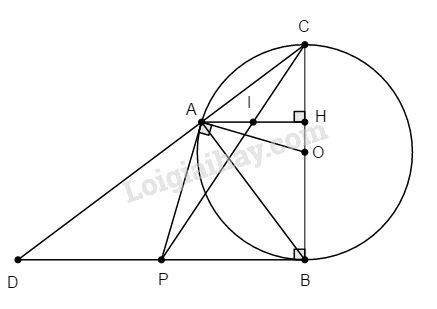
Gọi D là giao điểm của đường thẳng AC và BP.

Ta có: $\widehat {BAC} = 90^\circ$ (BC là đường kính)

$\Rightarrow \widehat {BAD} = 90^\circ$ (kề bù) hay $\widehat {DAP} + \widehat {PAB} = 90^\circ$ (1)

∆ABD vuông tại A (cmt) $\Rightarrow \widehat {ABD} + \widehat {ADB} = 90^\circ$ (2)

Mặt khác PA, PB là hai tiếp tuyến cuả (O)

nên $PA = PB$ và $\widehat {PAB} = \widehat {PBA}$ (3)

Từ (1), (2) và (3) $\Rightarrow \widehat {DAP} = \widehat {ADP}$

Do đó ∆APD cân tại P

$⇒ PA = PD$, mà $PA = PB$ (tính chất hai tiếp tuyến cắt nhau)

$⇒ PD = PB.$

Lại có DB // AH (⊥ BC)

Xét ∆PBC có : IH // PB $\Rightarrow {{IH} \over {PB}} = {{IC} \over {PC}}$ (4) (Định lí Ta-lét)

Tương tự ∆PCD có : AI // PD $\Rightarrow {{AI} \over {DP}} = {{IC} \over {PC}}$ (5)

Từ (4) và (5) $\Rightarrow {{IH} \over {PB}} = {{AI} \over {DP}} \Rightarrow IH = IA$ (vì $PB = PD$)