Đề thi giữa kì 2 Toán 8 - Đề số 6 - Cánh diều
Phần trắc nghiệm (3 điểm) Câu 1: Giải phương trình \(\frac{{7 - 2x}}{2} - \frac{2}{5}\left( {2 - x} \right) = 1\frac{1}{4}\) ta được:
Đề bài
Giải phương trình \(\frac{{7 - 2x}}{2} - \frac{2}{5}\left( {2 - x} \right) = 1\frac{1}{4}\) ta được:
-
A.
\(x = \frac{3}{{10}}\)
-
B.
\(x = \frac{2}{{12}}\)
-
C.
\(x = \frac{9}{4}\)
-
D.
\(x = \frac{{29}}{{12}}\)
Để biểu diễn tỉ lệ phần trăm của mỗi đối tượng trong tổng thể ta dùng biểu đồ nào sau đây?
-
A.
Biểu đồ tranh.
-
B.
Biểu đồ cột.
-
C.
Biểu đồ đoạn thẳng.
-
D.
Biểu đổ hình quạt tròn.
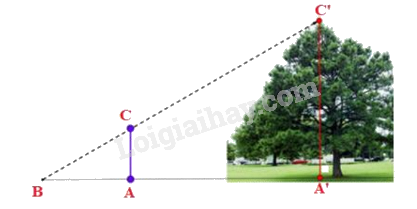
Hình dưới đây mô tả cách đo chiều cao của cây. Các thông số đo đạc được như sau: \(AB = 1m;AA' = 4,5m;CA = 1,2m\). Chiều cao của cây là
-
A.
\(5\left( m \right)\).
-
B.
\(4,5\left( {{\rm{\;m}}} \right)\).
-
C.
\(6,6\left( {{\rm{\;m}}} \right)\).
-
D.
\(4\left( {{\rm{\;m}}} \right)\).
Cho hình thoi \(ABCD\) có \(M\) là trung điểm của \(AD\), đường chéo \(AC\) cắt \(BM\) tại điểm \(E\).
Tỉ số \(\frac{{EM}}{{EB}}\) bằng:
-
A.
\(\frac{1}{3}\)
-
B.
2
-
C.
\(\frac{1}{2}\)
-
D.
\(\frac{2}{3}\)
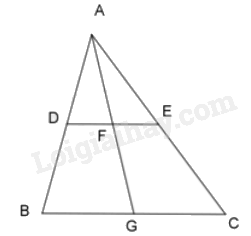
-
A.
\(\frac{{AD}}{{AB}} = \frac{{AG}}{{AF}} = \frac{{AC}}{{AE}}\)
-
B.
\(\frac{{AD}}{{AB}} = \frac{{AF}}{{AG}} = \frac{{AE}}{{EC}}\)
-
C.
\(\frac{{AD}}{{AB}} = \frac{{AF}}{{FG}} = \frac{{AE}}{{EC}}\)
-
D.
\(\frac{{AD}}{{AB}} = \frac{{AF}}{{AG}} = \frac{{AE}}{{AC}}\)
Tìm tất cả các số thực a sao cho \(x = 4\) là một nghiệm của phương trình:
\(x + 2a = 16 + ax - 6a\)
-
A.
\(a = 2\)
-
B.
\(a = 3\)
-
C.
\(a = - 1\)
-
D.
\(a = - 2\)
Một hộp có 1 quả bóng vàng, 1 quả bóng hồng và 1 quả bóng đỏ; các quả bóng có kích thước và khối lượng như nhau . Mỗi lần lấy ngẫu nhiên 1 quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Trong 45 lần lấy bóng liên tiếp, quả bóng vàng xuất hiện 5 lần; quả bóng hồng xuất hiện 10 lần. Tính xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng màu đỏ".
-
A.
\(\frac{2}{9}\)
-
B.
\(\frac{7}{{45}}\)
-
C.
\(\frac{2}{3}\)
-
D.
\(\frac{7}{9}\)
Cho hình sau, biết giữa hai điểm \(B\) và \(C\) có một hồ sâu. Khoảng cách giữa hai điểm \(D\) và \({\rm{E}}\) đo được là \(53{\rm{\;m}}\). Hỏi \({\rm{B}}\) và \({\rm{C}}\) cách nhau bao nhiêu mét?
-
A.
\(13,25\left( m \right)\)
-
B.
\(52\left( m \right)\)
-
C.
\(26,5\left( m \right)\)
-
D.
\(106\left( m \right)\)
Bạn An đi bộ với vận tốc không đổi trong 45 phút trước khi chạy bộ trong nửa giờ với vận tốc gấp đôi vận tốc đi bộ. Bạn An di chuyển được quãng đường tổng cộng dài \(7{\rm{\;km}}\). Tính vận tốc đi bộ của bạn An.
-
A.
\(3{\rm{\;km}}/{\rm{h}}\)
-
B.
\(3,2{\rm{\;km}}/{\rm{h}}\)
-
C.
\(4{\rm{\;km}}/{\rm{h}}\)
-
D.
\(4,5{\rm{\;km}}/{\rm{h}}\)
Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1;3;5; \ldots ;97\); 99; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố: "Số xuất hiện trên thẻ được rút ra là số lớn hơn 3 và là ước của 50 "
-
A.
\(\frac{9}{{50}}\)
-
B.
\(\frac{1}{{25}}\)
-
C.
\(\frac{7}{{99}}\)
-
D.
\(\frac{2}{{45}}\)
Lời giải và đáp án
Giải phương trình \(\frac{{7 - 2x}}{2} - \frac{2}{5}\left( {2 - x} \right) = 1\frac{1}{4}\) ta được:
-
A.
\(x = \frac{3}{{10}}\)
-
B.
\(x = \frac{2}{{12}}\)
-
C.
\(x = \frac{9}{4}\)
-
D.
\(x = \frac{{29}}{{12}}\)
Đáp án : D
Phương trình bậc nhất \(ax + b = 0\left( {a \ne 0} \right)\) được giải như sau:
\(ax + b = 0\)
\(ax = - b\)
\(x = - \frac{b}{a}\)
\(\frac{{7 - 2x}}{2} - \frac{2}{5}\left( {2 - x} \right) = 1\frac{1}{4}\)
\(\frac{{10\left( {7 - 2x} \right)}}{{20}} - \frac{{8\left( {2 - x} \right)}}{{20}} = \frac{{25}}{{20}}\)
\(70 - 20x - 16 + 8x = 25\)
\( - 20x + 8x = 25 - 70 + 16\)
\( - 12x = - 29\)
\(x = \frac{{29}}{{12}}\)
Đáp án D.
Để biểu diễn tỉ lệ phần trăm của mỗi đối tượng trong tổng thể ta dùng biểu đồ nào sau đây?
-
A.
Biểu đồ tranh.
-
B.
Biểu đồ cột.
-
C.
Biểu đồ đoạn thẳng.
-
D.
Biểu đổ hình quạt tròn.
Đáp án : D
Để biểu thị tỉ lệ phần trăm của từng loại số liệu với toàn thể, ta thường sử dụng biểu đồ hình quạt tròn.
Để biểu thị tỉ lệ phần trăm của từng loại số liệu với toàn thể, ta thường sử dụng biểu đồ hình quạt tròn.
Đáp án D.
Hình dưới đây mô tả cách đo chiều cao của cây. Các thông số đo đạc được như sau: \(AB = 1m;AA' = 4,5m;CA = 1,2m\). Chiều cao của cây là

-
A.
\(5\left( m \right)\).
-
B.
\(4,5\left( {{\rm{\;m}}} \right)\).
-
C.
\(6,6\left( {{\rm{\;m}}} \right)\).
-
D.
\(4\left( {{\rm{\;m}}} \right)\).
Đáp án : C
Áp dụng hệ quả định lí Thales: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ vơi ba cạnh của tam giác đã cho.
Từ hình vẽ, ta có: \(AC//A'C'\)
Xét \(\Delta BA'C'\) có \(AC//A'C'\), theo hệ quả định lí Thales, ta có: \(\frac{{AB}}{{BA'}} = \frac{{AC}}{{A'C'}}\) hay \(\frac{1}{{1 + 4,5}} = \frac{{1,2}}{{A'C'}}\)
suy ra \(A'C' = 1,2.5,5 = 6,6\left( m \right)\)
Vậy chiều cao của cây là 6,6m
Đáp án C.
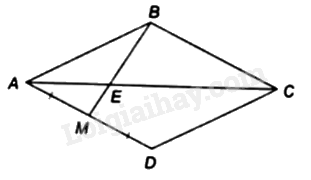
Cho hình thoi \(ABCD\) có \(M\) là trung điểm của \(AD\), đường chéo \(AC\) cắt \(BM\) tại điểm \(E\).

Tỉ số \(\frac{{EM}}{{EB}}\) bằng:
-
A.
\(\frac{1}{3}\)
-
B.
2
-
C.
\(\frac{1}{2}\)
-
D.
\(\frac{2}{3}\)
Đáp án : C
Tính chất của hình thoi (4 cạnh bằng nhau, đường chéo là phân giác của các góc)
Áp dụng tính chất của đường phân giác: Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với cạnh kề của hai đoạn ấy.
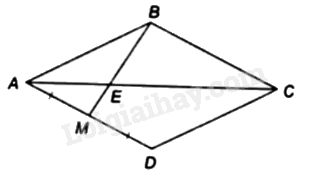
Vì tứ giác \({\rm{ABCD}}\) là hình thoi nên \({\rm{AC}}\) là tia phân giác của \(\widehat {BAD}\) và \(AD = AB\)
Xét \(\Delta ABM\) có \(AE\) là tia phân giác của \(\widehat {BAM}\)
Suy ra \(\frac{{EM}}{{EB}} = \frac{{AM}}{{AB}}\) (tính chất đường phân giác trong tam giác).
Mà \(M\) là trung điểm của \(AD\) nên \(AM = \frac{1}{2}AD = \frac{1}{2}AB\)
Do đó, \(\frac{{EM}}{{EB}} = \frac{{\frac{1}{2}AB}}{{AB}} = \frac{1}{2}\)
Đáp án C.
-
A.
\(\frac{{AD}}{{AB}} = \frac{{AG}}{{AF}} = \frac{{AC}}{{AE}}\)
-
B.
\(\frac{{AD}}{{AB}} = \frac{{AF}}{{AG}} = \frac{{AE}}{{EC}}\)
-
C.
\(\frac{{AD}}{{AB}} = \frac{{AF}}{{FG}} = \frac{{AE}}{{EC}}\)
-
D.
\(\frac{{AD}}{{AB}} = \frac{{AF}}{{AG}} = \frac{{AE}}{{AC}}\)
Đáp án : D
Áp dụng định lí Thales và tính chất bắc cầu để giải bài toán.
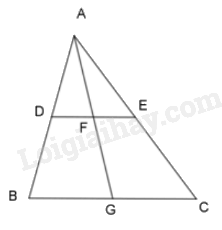
Ta có \(DE\parallel BC\) suy ra \(DF\parallel BG\) và \(FE\parallel GC\)
Vì \(DF\parallel BG\) áp dụng định lí Thales ta có: \(\frac{{AD}}{{AB}} = \frac{{AF}}{{AG}}\) (1)
Vì \(FE\parallel GC\) áp dụng định lí Thales ta có: \(\frac{{AF}}{{AG}} = \frac{{AE}}{{AC}}\) (2)
Từ (1) và (2) ta có: \(\frac{{AD}}{{AB}} = \frac{{AF}}{{AG}} = \frac{{AE}}{{AC}}\)
Đáp án D.
Tìm tất cả các số thực a sao cho \(x = 4\) là một nghiệm của phương trình:
\(x + 2a = 16 + ax - 6a\)
-
A.
\(a = 2\)
-
B.
\(a = 3\)
-
C.
\(a = - 1\)
-
D.
\(a = - 2\)
Đáp án : B
Số \({x_0}\) gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu giá trị của \(A\left( x \right)\) và \(B\left( x \right)\) tại \({x_0}\) bằng nhau.
Vì \(x = 4\) là nghiệm của phương trình \(x + 2a = 16 + ax - 6a\) nên:
\(4 + 2a = 16 + a.4 - 6a\)
\(4 + 2a = 16 + 4a - 6a\)
\(4 + 2a = 16 - 2a\)
\(2a + 2a = 16 - 4\)
\(4a = 12\)
\(a = 3\)
Vậy \(a = 3\)
Đáp án B.
Một hộp có 1 quả bóng vàng, 1 quả bóng hồng và 1 quả bóng đỏ; các quả bóng có kích thước và khối lượng như nhau . Mỗi lần lấy ngẫu nhiên 1 quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Trong 45 lần lấy bóng liên tiếp, quả bóng vàng xuất hiện 5 lần; quả bóng hồng xuất hiện 10 lần. Tính xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng màu đỏ".
-
A.
\(\frac{2}{9}\)
-
B.
\(\frac{7}{{45}}\)
-
C.
\(\frac{2}{3}\)
-
D.
\(\frac{7}{9}\)
Đáp án : C
Xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng màu đỏ" bằng tỉ số số lần xuất hiện quả bóng màu đỏ và số lần lấy bóng liên tiếp.
Trong 45 lần lấy bóng liên tiếp, quả bóng vàng xuất hiện 5 lần; quả bóng hồng xuất hiện 10 lần.
Suy ra số lần quả bóng đỏ xuất hiện là \(45 - 5 - 10 = 30\) lần
Xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng màu đỏ" là \(\frac{{30}}{{45}} = \frac{2}{3}\)
Đáp án C.
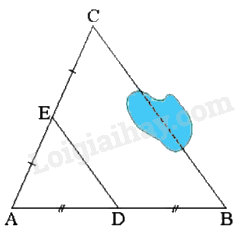
Cho hình sau, biết giữa hai điểm \(B\) và \(C\) có một hồ sâu. Khoảng cách giữa hai điểm \(D\) và \({\rm{E}}\) đo được là \(53{\rm{\;m}}\). Hỏi \({\rm{B}}\) và \({\rm{C}}\) cách nhau bao nhiêu mét?

-
A.
\(13,25\left( m \right)\)
-
B.
\(52\left( m \right)\)
-
C.
\(26,5\left( m \right)\)
-
D.
\(106\left( m \right)\)
Đáp án : D
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Đuờng trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Đường trung bình của tam giác thì song song vơi cạnh thứ ba và bằng nửa cạnh ấy.
Đáp án D.
Bạn An đi bộ với vận tốc không đổi trong 45 phút trước khi chạy bộ trong nửa giờ với vận tốc gấp đôi vận tốc đi bộ. Bạn An di chuyển được quãng đường tổng cộng dài \(7{\rm{\;km}}\). Tính vận tốc đi bộ của bạn An.
-
A.
\(3{\rm{\;km}}/{\rm{h}}\)
-
B.
\(3,2{\rm{\;km}}/{\rm{h}}\)
-
C.
\(4{\rm{\;km}}/{\rm{h}}\)
-
D.
\(4,5{\rm{\;km}}/{\rm{h}}\)
Đáp án : C
Giải bài toán bằng cách lập phương trình.
Bước 1: Lập phương trình:
Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số;
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
Toán về chuyển động đều: Quãng đường đi = Vận tốc \( \times \) Thời gian đi.
PT: Tổng quãng đường chạy là \(7{\rm{\;km}}\).
Đổi 45 phút \( = 0,75\) giờ; nửa giờ \( = 0,5\) giờ .
Gọi \(x\left( {{\rm{\;km}}/{\rm{h}}} \right)\) là vận tốc đi bộ của bạn An. Điều kiện: \(x > 0\).
Khi đó vận tốc chạy bộ của bạn An là \(2x\left( {{\rm{\;km}}/{\rm{h}}} \right)\).
Quãng đường bạn An đỉ bộ là \(0,75x\left( {{\rm{\;km}}} \right)\).
Quãng đường bạn An chạy bộ là \(2x \cdot 0,5 = x\left( {{\rm{\;km}}} \right)\).
Vì bạn An di chuyển quãng đường tổng cộng dài 7 km nên ta có PT:
\(\begin{array}{*{20}{r}}{}&{0,75x + x = 7}\\{}&{1,75x = 7}\\{}&{x = 4\left( {TM} \right)}\end{array}\)
Giá trị này của \(x\) thoả mãn điều kiện của ẩn.
Vậy vận tốc đi bộ của bạn An là 4 km/h.
Đáp án C.
Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1;3;5; \ldots ;97\); 99; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố: "Số xuất hiện trên thẻ được rút ra là số lớn hơn 3 và là ước của 50 "
-
A.
\(\frac{9}{{50}}\)
-
B.
\(\frac{1}{{25}}\)
-
C.
\(\frac{7}{{99}}\)
-
D.
\(\frac{2}{{45}}\)
Đáp án : B
Trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng, xác suất của một biến cố bằng tỉ số của số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.
Các kết quả thuận lợi cho biến cố "Số xuất hiện trên thẻ được rút ra là số lớn hơn 3 và là ước của 50 " là: {5; \(25\} \)
Suy ra có 2 kết quả thuận lợi cho biến cố đó.
Xác suất của biến cố đó là \(\frac{2}{{50}} = \frac{1}{{25}}\).
Đáp án B.
Phương trình bậc nhất \(ax + b = 0\left( {a \ne 0} \right)\) được giải như sau: \(ax + b = 0\)
\(ax = - b\)
\(x = - \frac{b}{a}\)
a) \(\frac{x}{2} - \frac{1}{5} = 2 - \frac{x}{3}\)
\(\frac{{15x - 6}}{{30}} = \frac{{60 - 10x}}{{30}}\)
\(15x - 6 = 60 - 10x\)
\(15x + 10x = 60 + 6\)
\(25x = 66\)
\(x = \frac{{66}}{{25}}\)
Vậy nghiệm của phương trình là \(x = \frac{{66}}{{25}}\) b) \(1 - \frac{{x + 5}}{3} = \frac{{3\left( {x - 1} \right)}}{4}\)
\(\frac{{12 - 4\left( {x + 5} \right)}}{{12}} = \frac{{9\left( {x - 1} \right)}}{{12}}\)
\(12 - 4x - 20 = 9x - 9\)
\( - 4x - 9x = - 9 - 12 + 20\)
\( - 13x = - 1\)
\(x = \frac{1}{{13}}\)
Vậy nghiệm của phương trình là \(x = \frac{1}{{13}}\) c) \(\frac{{6\left( {x - 2} \right)}}{7} - 12 = \frac{{2\left( {x - 7} \right)}}{3}\)
\(\frac{{18\left( {x - 2} \right) - 252}}{{21}} = \frac{{14\left( {x - 7} \right)}}{3}\)
\(18x - 36 - 252 = 14x - 98\)
\(18x - 14x = 36 + 252 - 98\)
\(4x = 190\)
\(x = \frac{{190}}{4} = \frac{{95}}{2}\)
Vậy nghiệm của phương trình là \(x = \frac{{95}}{2}\)

Năm nay tổng số công nhân của hai phân xưởng là 285 người.
Gọi số công nhân năm ngoái của phân xưởng \(I\) là \(x\) (người, \(x \in {N^{\rm{*}}}\) )
Số công nhân năm ngoái của phân xường II là \(270 - x\) (người)
Số công nhân năm nay của phân xưởng \(I\) là: \(x + 5{\rm{\% }}x = 1,05x\) (người)
Số công nhân năm nay của phân xưởng II là: \(\left( {270 - x} \right) + \left( {270 - x} \right).6{\rm{\% }} = 1,06\left( {270 - x} \right)\) (người)
Năm nay, tổng số công nhân của hai phân xưởng là 285 người nên ta có:
\(1,05x + 1,06\left( {270 - x} \right) = 285\)
\(1,05x + 286,2 - 1,06x = 285\)
\( - 0,01x = - 1,2\)
\(x = 120\left( {TM} \right)\)
Số công nhân năm nay của phân xưởng I là: 1,05.120=126 (công nhân)
Số công nhân năm nay của phân xưởng II là: 285 - 126 = 159 (công nhân)
Vậy năm nay, xưởng I có 126 công nhân, xưởng II có 159 công nhân.
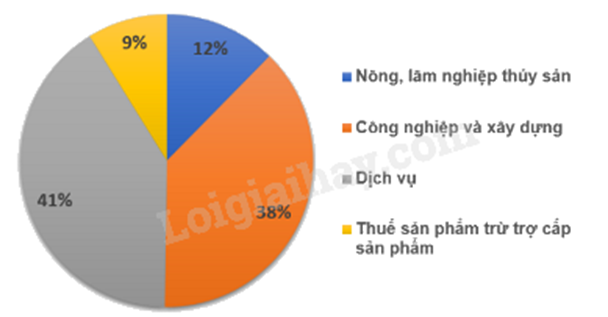
Phát hiện vấn đề qua phân tích dữ liệu thống kê từ biểu đồ.
Lĩnh vực đóng góp nhiều nhất vào GDP là dịch vụ, với 40,95%
Lĩnh vực dịch vụ đóng góp: 400.40,95% =163,8 (tỉ đô la Mỹ)
Xác suất thực nghiệm của biến cố "Mặt xuất hiện của đồng xu là mặt 4 chấm" là tỉ số giữa số lần xuất hiện mặt 4 chấm và số lần gieo xúc xắc.
Xác suất thực nghiệm của biến cố "Mặt xuất hiện có số chấm là số chẵn chia hết cho 3" là tỉ số giữa số lần xuất hiện mặt số chẵn chia hết cho 3 và số lần gieo xúc xắc.
Xác suất thực nghiệm của biến cố "Mặt xuất hiện có số chấm là số lẻ là ước của 6" là tỉ số giữa số lần xuất hiện mặt số lẻ là ước của 6 và số lần gieo xúc xắc.
Gieo xúc xắc 100 lần.
Có 14 lần xuất hiện mặt 4 chấm.
Xác suất của thực nghiệm của biến cố "Mặt xuất hiện là mặt 4" là \(\frac{{14}}{{100}} = \frac{7}{{50}}\)
b) "Mặt xuất hiện có số chấm là số chẵn chia hết cho 3" là mặt 6 chấm
Có 20 lần xuất hiện mặt có số chấm là số chã̃n chia hết cho 3
Xác suất của biển cố "Mặt xuất hiện có số chấm là số chẵn chia hết cho 3 " là \(\frac{{20}}{{100}} = \frac{1}{5}\)
c) "Mặt xuất hiện có số chấm là số lẻ và là ước của 6" là mặt 1 chấm, mặt 3 chấm
Có \(17 + 15\) = 32 lần xuất hiện mặt có có số chấm là số lẻ và là ước của 6
Xác suất của thực nghiệm của biến cố "Mặt xuất hiện có số chấm là số lẻ và là ước của 6 " là \(\frac{{32}}{{100}} = \frac{8}{{25}}\)
Định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Định lí Thales đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
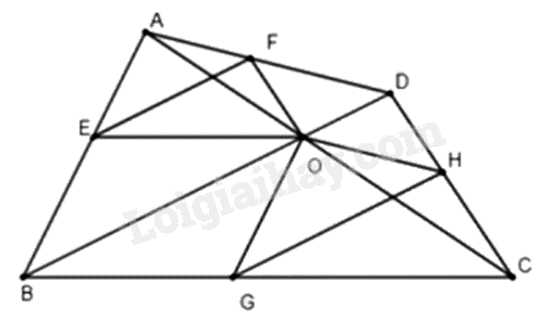
a) Xét \(\Delta ADC\) có \(OF//DC\), theo định lí Thales suy ra \(\frac{{AF}}{{AD}} = \frac{{AO}}{{AC}}\left( 1 \right)\)
Xét \(\Delta ABC\) có \(OE//BC\), theo định lí Thales ta có \(\frac{{AE}}{{AB}} = \frac{{AO}}{{AC}}\left( 2 \right)\)
Từ (1),(2) suy ra \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AB}}\)
Theo định lí Thales đảo trong \(\Delta ADB\) có: \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AB}}\) suy ra \(EF//BD\left( {{\rm{dpcm}}} \right)\)
b) Xét \(\Delta ADC\) có \(OH//AD\), theo định lí Thales ta có \(\frac{{CH}}{{CD}} = \frac{{CO}}{{AC}}\left( 3 \right)\)
Xét \(\Delta ABC\) có \(OG//AB\), theo định lí Thales ta có \(\frac{{CG}}{{BC}} = \frac{{CO}}{{AC}}\left( 4 \right)\)
Từ (3),(4) suy ra \(\frac{{CH}}{{CD}} = \frac{{CG}}{{BC}}\)
Theo định lí Thales đảo suy ra \(GH//BD\).
Xét \(\Delta BCD\) có \(GH//BD\), theo định lí Thales ta có \(\frac{{CH}}{{DH}} = \frac{{CG}}{{BG}}\) suy ra \(CH \cdot BG = DH \cdot CG\left( {{\rm{dpcm}}} \right)\).