Giải bài 10 trang 22 sách bài tập toán 12 - Chân trời sáng tạo
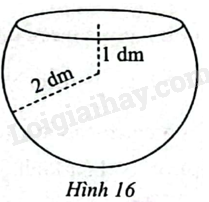
Một bể cá có dạng là một phần hình cầu được tạo thành khi cắt hình cầu bán kính 2 dm bằng mặt phẳng cách tâm của hình cầu 1 dm (Hình 16). Tính dung tích của bể cá (kết quả làm tròn đến hàng phần mười của đềximét khối). Gợi ý: Có thể coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số (y = sqrt {4 - {x^2}} ) với ( - 2 le x le 1), trục hoành và đường thẳng (x = 1) quanh trục hoành.
Đề bài
Một bể cá có dạng là một phần hình cầu được tạo thành khi cắt hình cầu bán kính 2 dm bằng mặt phẳng cách tâm của hình cầu 1 dm (Hình 16). Tính dung tích của bể cá (kết quả làm tròn đến hàng phần mười của đềximét khối).
Gợi ý: Có thể coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {4 - {x^2}} \) với \( - 2 \le x \le 1\), trục hoành và đường thẳng \(x = 1\) quanh trục hoành.
Phương pháp giải - Xem chi tiết
Gắn parabol vào hệ trục toạ độ \(Oxy\), sau đó sử dụng công thức: Tính thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) quay quanh trục \(Ox\) là: \(V = \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} \).
Lời giải chi tiết
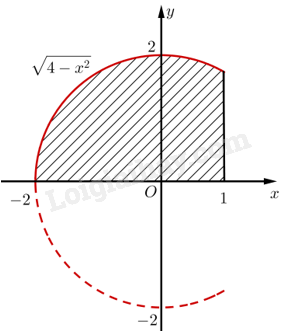
Chọn hệ trục toạ độ \(Oxy\) như hình vẽ.
Coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {4 - {x^2}} \) với \( - 2 \le x \le 1\), trục hoành và đường thẳng \(x = 1\) quanh trục hoành.
Dung tích của bể cá là:
\(V = \pi \int\limits_{ - 2}^1 {{{\left( {\sqrt {4 - {x^2}} } \right)}^2}dx} = \pi \int\limits_{ - 2}^1 {\left( {4 - {x^2}} \right)dx} = \left. {\pi \left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 2}^1 = 9\pi \approx 28,3\left( {d{m^3}} \right)\).