Giải bài 10 trang 24 sách bài tập toán 12 - Chân trời sáng tạo
Chọn đúng hoặc sai cho mỗi ý a, b, c, d. Cho (y = fleft( x right)) là hàm số bậc hai có đồ thị như Hình 1. Gọi (S) là diện tích của hình phẳng giới hạn bởi đồ thị của hàm số (y = fleft( x right)) và trục hoành. a) (fleft( x right) = 4 - 2{x^2}). b) (S = intlimits_{ - 2}^2 {left| {fleft( x right)} right|dx} ). c) (S = intlimits_{ - 2}^2 {fleft( x right)dx} ). d) (S = frac{{16}}{3}).
Đề bài
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.
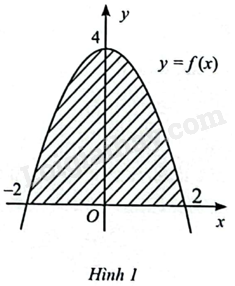
Cho \(y = f\left( x \right)\) là hàm số bậc hai có đồ thị như Hình 1. Gọi \(S\) là diện tích của hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\) và trục hoành.
a) \(f\left( x \right) = 4 - 2{x^2}\).
b) \(S = \int\limits_{ - 2}^2 {\left| {f\left( x \right)} \right|dx} \).
c) \(S = \int\limits_{ - 2}^2 {f\left( x \right)dx} \).
d) \(S = \frac{{16}}{3}\).
Phương pháp giải - Xem chi tiết
Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết
Giả sử hàm số có dạng \(f\left( x \right) = a{x^2} + c\left( {a < 0} \right)\).
Đồ thị hàm số đi qua điểm \(\left( {0;4} \right)\) nên ta có \(c = 4\).
Đồ thị hàm số đi qua điểm \(\left( {2;0} \right)\) nên ta có \(a{.2^2} + 4 = 0 \Leftrightarrow a = - 1\).
Vậy hàm số đó là \(f\left( x \right) = - {x^2} + 4\). Vậy a) sai.
Ta có \(S = \int\limits_{ - 2}^2 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - 2}^2 {f\left( x \right)dx} = \int\limits_{ - 2}^2 {\left( { - {x^2} + 4} \right)dx} = \left. {\left( { - \frac{{{x^3}}}{3} + 4x} \right)} \right|_{ - 2}^2 = \frac{{32}}{3}\).
Vậy b) đúng, c) đúng, d) sai.
a) S.
b) Đ.
c) Đ.
d) S.