Giải bài 5 trang 74 sách bài tập toán 8 - Cánh diều — Không quảng cáo

Đề bài

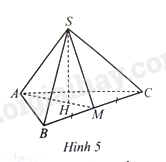
Cho hình chóp tam giác đều $S.ABC$ có độ dài cạnh đáy bằng 9 cm, $SH$ là chiều cao. Gọi $M$ là trung điểm của $BC$ (Hình 5). Tính thể tích của hình chóp $S.ABC$, biết $H$ là trọng tâm của tam giác $ABC$, $AH = \frac{{\sqrt 3 }}{3}AB$ và $SH = 2AH$.

Lời giải chi tiết

Ta có: $AH = \frac{{\sqrt 3 }}{3}AB$ nên $AH = 3\sqrt 3$ cm. Suy ra $SH = 2AH = 6\sqrt 3$ cm.

Do $H$ là trọng tâm của tam giác $ABC$ nên $AH = \frac{2}{3}AM$.

Suy ra $AM = \frac{3}{2}AH = \frac{{9\sqrt 3 }}{2}$ cm.

$\Delta ABM = \Delta ACM$(c-c-c) suy ra $\widehat {AMB} = \widehat {AMC} = 90^\circ$. Do đó $AM \bot BC$.

Diện tích của hình chóp tam giác đều đó là:

${S_{ABC}} = \frac{1}{2}.BC.AM = \frac{{81\sqrt 3 }}{4}\left( {c{m^2}} \right)$

Thể tích của hình chóp tam giác đều đó là: $\frac{1}{3}.{S_{ABC}}.SH = \frac{{243}}{2}\left( {c{m^3}} \right)$.