Giải bài 6 trang 36 sách bài tập toán 12 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Nam dùng một tấm bìa có kích thước 50 cm × 20 cm để làm một chiếc lon hình trụ (không có nắp).

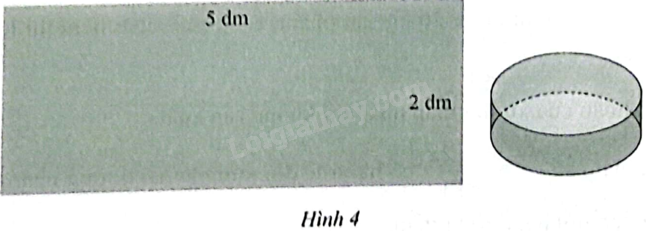
Hỏi cần chọn bán kính đáy hình trụ là bao nhiêu xăngtimét thì lon hình trụ đạt thể tích lớn nhất?

Lưu ý: Kết quả làm tròn đến hàng phần trăm của xăngtimét, bỏ qua phần hao hụt khi cắt và tạo hình, đáy và mặt bên phải là các bìa nguyên vẹn (không ghép nối).

Lời giải chi tiết

Gọi \(x\) (dm) là bán kính đáy hình trụ \(\left( {x > 0} \right)\).

• Phương án 1:

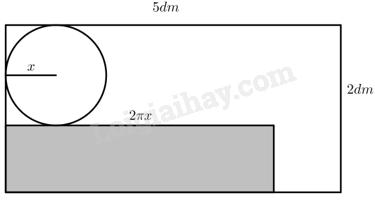
Khi đó chiều cao của hình trụ là: \(2 - 2{\rm{x}}\left( {dm} \right)\).

Chu vi đáy của hình trụ là: \(2\pi {\rm{x}}\left( {dm} \right)\).

Vì chu vi đáy của hình trụ không được vượt quá 5 dm nên ta có: \(2\pi x \le 5 \Leftrightarrow x \le \frac{5}{{2\pi }}\).

Thể tích của hình trụ là: \(V\left( x \right) = \pi {x^2}\left( {2 - 2{\rm{x}}} \right) =  - 2\pi {{\rm{x}}^3} + 2\pi {{\rm{x}}^2}\left( {d{m^3}} \right)\).

Xét hàm số \(V\left( x \right) =  - 2\pi {{\rm{x}}^3} + 2\pi {{\rm{x}}^2}\) trên nửa khoảng \(\left( {0;\frac{5}{{2\pi }}} \right]\).

Ta có: \(V'\left( x \right) =  - 6\pi {{\rm{x}}^2} + 4\pi {\rm{x}}\)

\(V'\left( x \right) = 0 \Leftrightarrow x = 0\) hoặc \(x = \frac{2}{3}\).

Bảng biến thiên:

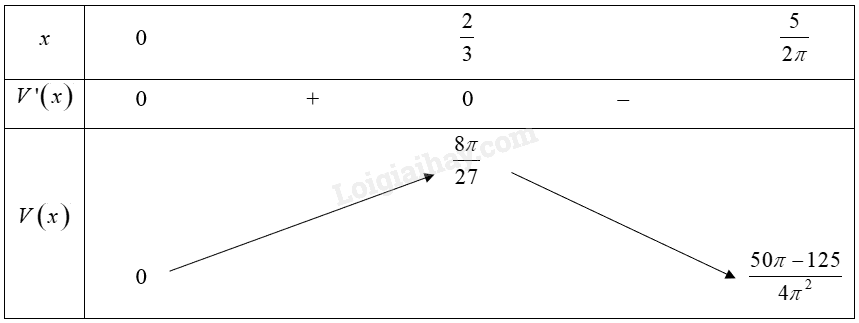
Vậy \(\mathop {\max }\limits_{\left( {0;\frac{5}{{2\pi }}} \right]} V\left( x \right) = V\left( {\frac{2}{3}} \right) = \frac{{8\pi }}{{27}} \approx 0,93\).

Vậy với \(x = \frac{2}{3}\left( {dm} \right)\) thì thể tích của hình trụ là lớn nhất bằng \(0,93\left( {d{m^3}} \right)\).

• Phương án 2:

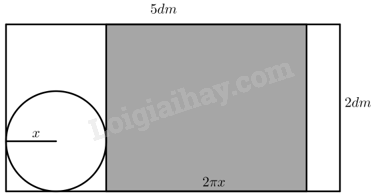
Khi đó chiều cao của hình trụ là: \(2\left( {dm} \right)\).

Chu vi đáy của hình trụ là: \(2\pi {\rm{x}}\left( {dm} \right)\).

Vì tổng đường kính và chu vi đáy của hình trụ không được vượt quá 5 dm nên ta có:

\(2\pi x + 2{\rm{x}} \le 5 \Leftrightarrow 2{\rm{x}}\left( {\pi  + 1} \right) \le 5 \Leftrightarrow x \le \frac{5}{{2\left( {\pi  + 1} \right)}}\).

Thể tích của hình trụ là: \(V\left( x \right) = \pi {x^2}2 = 2\pi {{\rm{x}}^2}\left( {d{m^3}} \right)\).

Xét hàm số \(V\left( x \right) = 2\pi {{\rm{x}}^2}\) trên nửa khoảng \(\left( {0;\frac{5}{{2\left( {\pi  + 1} \right)}}} \right]\).

Ta có: \(V'\left( x \right) = 4\pi {\rm{x}}\)

\(V'\left( x \right) = 0 \Leftrightarrow x = 0\).

Bảng biến thiên:

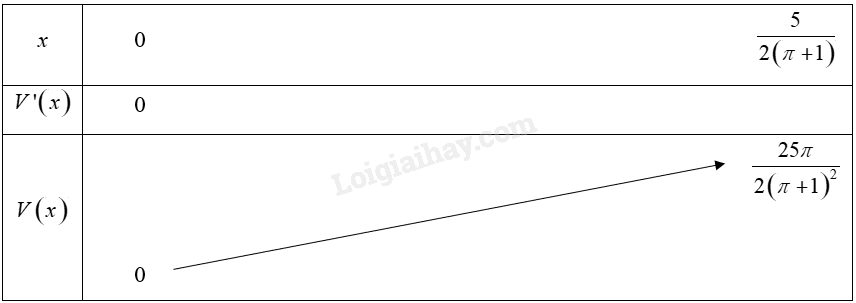
Vậy \(\mathop {\max }\limits_{\left( {0;\frac{5}{{2\pi }}} \right]} V\left( x \right) = V\left( {\frac{5}{{2\left( {\pi  + 1} \right)}}} \right) = \frac{{25\pi }}{{2{{\left( {\pi  + 1} \right)}^2}}} \approx 2,29\).

Vậy với \(x = \frac{5}{{2\left( {\pi  + 1} \right)}}\left( {dm} \right)\) thì thể tích của hình trụ là lớn nhất bằng \(2,29\left( {d{m^3}} \right)\).

Vậy thể tích lon hình trụ lớn nhất khi thiết kế theo phương án 2 và bán kính đáy khoảng \(\frac{5}{{2\left( {\pi  + 1} \right)}} \approx 0,60\left( {dm} \right)\).