Đề thi giữa kì 2 Toán 8 - Đề số 5 - Chân trời sáng tạo
Phần trắc nghiệm (3 điểm) Câu 1 (150991): Cho đường thẳng d: y = 2x + 1. Hệ số góc của đường thẳng d là?
Đề bài
Cho đường thẳng d: y = 2x + 1. Hệ số góc của đường thẳng d là?
-
A.
-2.
-
B.
1.
-
C.
\(\frac{1}{2}\).
-
D.
2.
Cho đường thẳng d : y = -3x + 2. Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Diện tích tam giác OAB là :
-
A.
\(\frac{4}{3}\).
-
B.
\(\frac{{ - 2}}{3}\).
-
C.
\(\frac{3}{2}\).
-
D.
\(\frac{2}{3}\).
Cho hàm số \(y = f\left( x \right) = \frac{1}{2}x + 5\), giá trị \(f\left( 0 \right)\) là:
-
A.
-5.
-
B.
0.
-
C.
5.
-
D.
10.
Cho \(y = \left( {m - 3} \right)x + 7\), hàm số không phải là hàm bậc nhất khi m bằng:
-
A.
1.
-
B.
3.
-
C.
-3.
-
D.
0.
Cho\(y = \left( {m + 3} \right)x - 2\), giá trị của m để hàm số có hệ số góc âm trên \(\mathbb{R}\) là:
-
A.
0.
-
B.
3.
-
C.
-1.
-
D.
-4.
Góc tạo bởi đường thẳng \(y = - x + 5\) và trục Ox là:
-
A.
\({45^0}\).
-
B.
\({90^0}\).
-
C.
\({120^0}\).
-
D.
\({60^0}\).
Tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Vẽ ME, NF cùng vuông góc với BC (E, F thuộc BC). Khẳng định sai là:
-
A.
MN // EF.
-
B.
ME = NF.
-
C.
MN = ME.
-
D.
MN = EF.
Cho tam giác ABC có chu vi 80cm. Gọi D, E, F là trung điểm của các cạnh AB, AC, BC. Chu vi tam giác DEF là:
-
A.
40cm.
-
B.
160cm.
-
C.
80cm.
-
D.
20cm.
-
A.
6.
-
B.
4.
-
C.
2.
-
D.
1.
Để tính chiều cao AB của ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây ED = 2m và biết được các khoảng cách AE = 4m, EC = 2,5m.
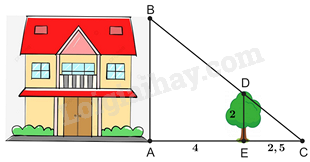
Khi đó chiều cao AB của ngôi nhà là:
-
A.
5,2m.
-
B.
8,125m.
-
C.
4m.
-
D.
6,5m.
-
A.
5,5.
-
B.
10.
-
C.
3.
-
D.
1,75.
-
A.
20.
-
B.
51,2.
-
C.
15.
-
D.
11,25.
Lời giải và đáp án
Cho đường thẳng d: y = 2x + 1. Hệ số góc của đường thẳng d là?
-
A.
-2.
-
B.
1.
-
C.
\(\frac{1}{2}\).
-
D.
2.
Đáp án : D
Dựa vào kiến thức về hệ số góc của đường thẳng.
Đường thẳng d: y = 2x + 1 có hệ số góc là 2.
Cho đường thẳng d : y = -3x + 2. Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Diện tích tam giác OAB là :
-
A.
\(\frac{4}{3}\).
-
B.
\(\frac{{ - 2}}{3}\).
-
C.
\(\frac{3}{2}\).
-
D.
\(\frac{2}{3}\).
Đáp án : D
Xác định tọa độ của điểm A, B. Sử dụng công thức tính diện tích tam giác.
Giao điểm của đường thẳng d với trục hoành là: 0 = -3x + 2 hay x = \(\frac{2}{3}\) => \(A\left( {\frac{2}{3};0} \right)\).
Giao điểm của đường thẳng d với trục tung là: y = -3.0 + 2 hay y = 2 => \(B\left( {0;2} \right)\).
Suy ra \(\left| {OA} \right| = \left| {\frac{2}{3}} \right| = \frac{2}{3};\left| {OB} \right| = \left| 2 \right| = 2\).
Vì tam giác OAB vuông tại O nên diện tích tam giác OAB là:
\({S_{\Delta ABC}} = \frac{1}{2}.\frac{2}{3}.2 = \frac{2}{3}\)(đvdt).
Cho hàm số \(y = f\left( x \right) = \frac{1}{2}x + 5\), giá trị \(f\left( 0 \right)\) là:
-
A.
-5.
-
B.
0.
-
C.
5.
-
D.
10.
Đáp án : C
Thay x = 0 để tìm f(0).
Giá trị \(f\left( 0 \right)\) là: \(f\left( 0 \right) = \frac{1}{2}.0 + 5 = 5\).
Cho \(y = \left( {m - 3} \right)x + 7\), hàm số không phải là hàm bậc nhất khi m bằng:
-
A.
1.
-
B.
3.
-
C.
-3.
-
D.
0.
Đáp án : B
Hàm số bậc nhất là hàm số có dạng \(y = ax + b\left( {a \ne 0} \right)\) nên hàm số không phải hàm số bậc nhất nếu \(a = 0\).
Hàm số \(y = \left( {m - 3} \right)x + 7\) không là hàm số bậc nhất khi \(m - 3 = 0 \Rightarrow m = 3\).
Cho\(y = \left( {m + 3} \right)x - 2\), giá trị của m để hàm số có hệ số góc âm trên \(\mathbb{R}\) là:
-
A.
0.
-
B.
3.
-
C.
-1.
-
D.
-4.
Đáp án : D
Hàm số bậc nhất là hàm số có dạng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là a.
Hệ số góc âm có nghĩa là a < 0.
Để hàm số có hệ số góc âm trên \(\mathbb{R}\) thì \(m + 3 < 0 \Leftrightarrow m < - 3\). Trong các giá trị trên chỉ có -4 là thỏa mãn.
Góc tạo bởi đường thẳng \(y = - x + 5\) và trục Ox là:
-
A.
\({45^0}\).
-
B.
\({90^0}\).
-
C.
\({120^0}\).
-
D.
\({60^0}\).
Đáp án : D
Vẽ đồ thị hàm số để xác định.
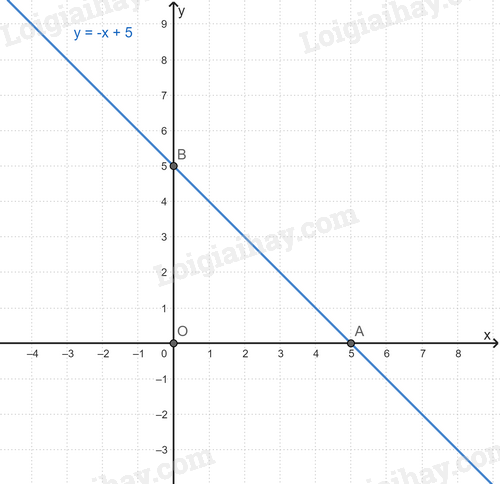
Quan sát đồ thị hàm số \(y = - x + 5\), ta thấy đồ thị tạo với hai trục tọa độ một tam giác vuông cân tại O, khi đó \(\widehat {OAB} = \widehat {OBA} = {45^0}\)\( \Rightarrow \) Góc tạo bởi đường thẳng \(y = - x + 5\) và trục Ox bằng \({45^0}\).
Tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Vẽ ME, NF cùng vuông góc với BC (E, F thuộc BC). Khẳng định sai là:
-
A.
MN // EF.
-
B.
ME = NF.
-
C.
MN = ME.
-
D.
MN = EF.
Đáp án : C
Dựa vào kiến thức về đường trung bình trong tam giác và dấu hiệu nhận biết hình học.
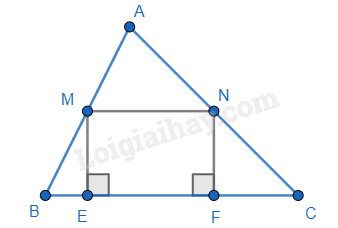
Ta có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC nên MN // BC và MN = \(\frac{1}{2}\)BC. => MN // EF (E,F \( \in \) BC) nên A đúng.
Ta có ME \( \bot \) BC, NF \( \bot \) BC => ME // NF.
Tứ giác MNFE có MN // EF (E,F \( \in \) BC); ME // NF nên MNFE là hình bình hành.
=> MN = EF; ME = NF (cặp cạnh tương ứng) nên B và D đúng.
MN = ME không có đủ điều kiện để xác định nên C sai.
Cho tam giác ABC có chu vi 80cm. Gọi D, E, F là trung điểm của các cạnh AB, AC, BC. Chu vi tam giác DEF là:
-
A.
40cm.
-
B.
160cm.
-
C.
80cm.
-
D.
20cm.
Đáp án : A
Sử dụng tính chất của đường trung bình để tính.
Ta có D, E, F là trung điểm của các cạnh AB, AC, BC nên DE, EF và DF là đường trung bình của tam giác ABC => \(DE = \frac{1}{2}BC;EF = \frac{1}{2}AB;DF = \frac{1}{2}AC\).
=> Chu vi tam giác DEF là: DE + EF + DF = \(\frac{1}{2}\)BC + \(\frac{1}{2}\)AB + \(\frac{1}{2}\)AC = \(\frac{1}{2}\)(BC + AB + AC) = \(\frac{1}{2}\).80 = 40(cm).
-
A.
6.
-
B.
4.
-
C.
2.
-
D.
1.
Đáp án : C
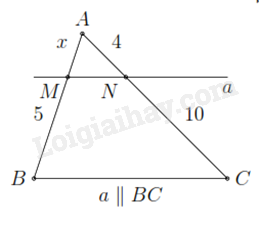
Sử dụng định lí Thales.
Do a // BC, áp dụng định lí Thales ta có:
\(\begin{array}{l}\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\\\frac{x}{5} = \frac{4}{{10}}\\x = 2\end{array}\)
Để tính chiều cao AB của ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây ED = 2m và biết được các khoảng cách AE = 4m, EC = 2,5m.

Khi đó chiều cao AB của ngôi nhà là:
-
A.
5,2m.
-
B.
8,125m.
-
C.
4m.
-
D.
6,5m.
Đáp án : A
Áp dụng hệ quả của định lí Thales trong tam giác để tính AB.
Vì ngôi nhà và cái cây cùng vuông góc với mặt đất nên chúng song song với nhau \( \Rightarrow AB//DE\).
Xét tam giác ABC có \(AB//DE\) nên ta có:
\(\frac{{AB}}{{AC}} = \frac{{DE}}{{EC}}\) (hệ quả của định lí Thales)
\( \Rightarrow AB = \frac{{DE}}{{EC}}.AC = \frac{2}{{2,5}}.\left( {4 + 2,5} \right) = 5,2\left( m \right)\)
-
A.
5,5.
-
B.
10.
-
C.
3.
-
D.
1,75.
Đáp án : A
Áp dụng tính chất của đường trung bình trong tam giác.
Xét tam giác ABC có:
D là trung điểm của AB (AD = DB)
E là trung điểm của AC (AE = EC)
\( \Rightarrow DE\) là đường trung bình của tam giác ABC.
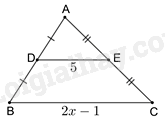
\(\begin{array}{l} \Rightarrow DE = \frac{1}{2}\left( {2x - 1} \right)\\5 = x - \frac{1}{2}\\x = 5,5\end{array}\)
-
A.
20.
-
B.
51,2.
-
C.
15.
-
D.
11,25.
Đáp án : A
Dựa vào tính chất tia phân giác trong tam giác.
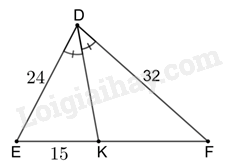
Ta có DK là tia phân giác của góc EDF nên \(\frac{{DE}}{{EK}} = \frac{{DF}}{{KF}} \Rightarrow KF = DF:\frac{{DE}}{{EK}} = 32:\frac{{24}}{{15}} = 20\).
a) Dựa vào kiến thức về vị trí tương đối của hai đường thẳng:
Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau khi và chỉ khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\).
b) Thay m vào \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\). Lấy hai điểm thuộc đồ thị hàm số để vẽ.
a) Để \(\left( {{d_1}} \right)//\left( {{d_2}} \right)\) thì:
\(\begin{array}{l}\left\{ \begin{array}{l}\frac{{m - 1}}{2} = m + 3\\ - m - 5 \ne - 2m + 7\end{array} \right.\\\left\{ \begin{array}{l}m - 1 = 2m + 6\\m \ne 12\end{array} \right.\\\left\{ \begin{array}{l}m = - 7\\m \ne 12\end{array} \right.\end{array}\)
Vậy m = -7 thì \(\left( {{d_1}} \right)//\left( {{d_2}} \right)\).
b) Thay m = -7 vào \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\), ta được:
\(\left( {{d_1}} \right):y = \frac{{ - 7 - 1}}{2}x - \left( { - 7} \right) - 5 = - 4x + 2\)
\(\left( {{d_2}} \right):y = \left( { - 7 + 3} \right)x - 2.\left( { - 7} \right) + 7 = - 4x + 21\)
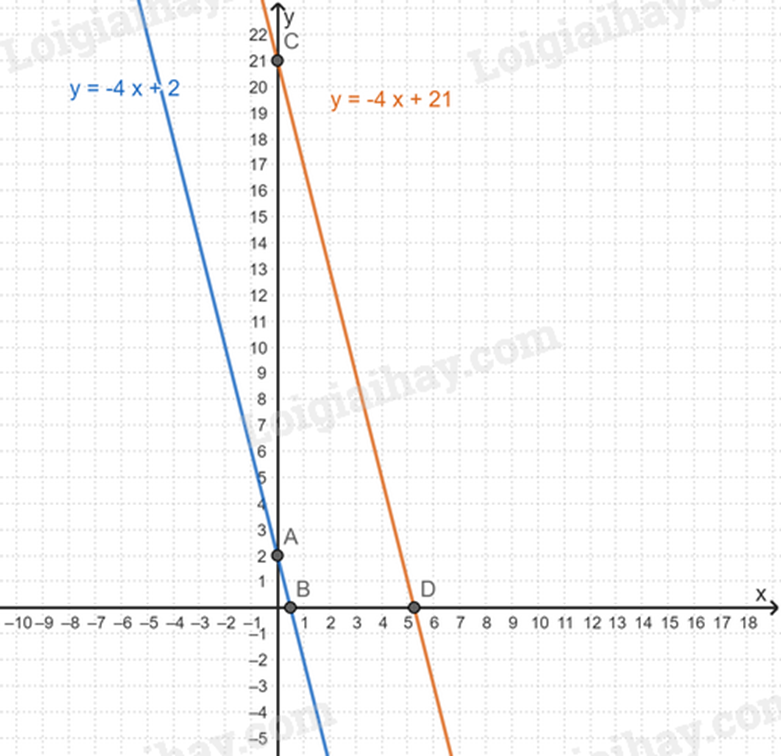
Vẽ \(\left( {{d_1}} \right):y = - 4x + 2\)
+ Cho x = 0 thì y = -4.0 + 2 = 2. Ta được điểm A(0; 2).
+ Cho y = 0 thì 0 = -4x + 2 => x =\(\frac{1}{2}\). Ta được điểm \(B\left( {\frac{1}{2};0} \right)\).
Đường thẳng AB chính là đường thẳng \(\left( {{d_1}} \right)\).
Vẽ \(\left( {{d_2}} \right):y = - 4x + 21\)
+ Cho x = 0 thì y = -4.0 + 21 = 21. Ta được điểm C(0; 21).
+ Cho y = 0 thì 0 = -4x + 21 => x =\(\frac{{21}}{4}\). Ta được điểm \(D\left( {\frac{{21}}{4};0} \right)\).
Đường thẳng CD chính là đường thẳng \(\left( {{d_2}} \right)\).
Ta có \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) như sau:
a) Thay F = 30 vào công thức để tìm C.
b) Thay C = 20 vào công thức để tìm F.
a) Ta có: \(C = \frac{5}{9}(F - 32) \Leftrightarrow C = \frac{5}{9}F - \frac{{160}}{9}\) (*)
Hàm số \(C = \frac{5}{9}F - \frac{{160}}{9}\) (theo biến số F) có dạng \(y = ax + b\) với \(a = \frac{5}{9} \ne 0\), \(b = - \frac{{160}}{9}\) nên \(C = \frac{5}{9}F - \frac{{160}}{9}\) là hàm số bậc nhất theo biến số \({\rm{F}}\).
b) Khi \({\rm{F}} = 30\), thế vào \(\left( * \right) \Rightarrow C = \frac{5}{9}.30 - \frac{{160}}{9} = - \frac{{10}}{9}\left( {^0{\rm{C}}} \right)\)
Khi \({\rm{F}} = 80\), thế vào \(\left( * \right) \Rightarrow C = \frac{5}{9}.80 - \frac{{160}}{9} = \frac{{80}}{3}\left( {^0{\rm{C}}} \right)\)
c) Khi \({\rm{C}} = - 10\left( {^0{\rm{C}}} \right)\), thế vào \(\left( * \right)\) ta có:
\(\begin{array}{l} - 10 = \frac{5}{9} \cdot F - \frac{{160}}{9}\\\frac{5}{9} \cdot F = - 10 + \frac{{160}}{9}\\\frac{5}{9} \cdot F = \frac{{70}}{9}\\F = \frac{{70}}{9}:\frac{5}{9}\\F = 14\end{array}\)
Dựa vào tính chất của đường trung bình để tính.
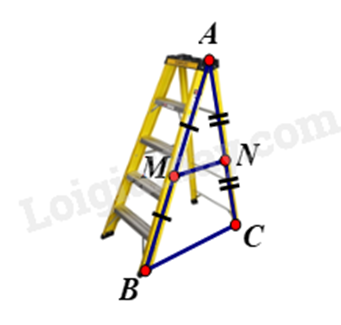
Gọi MN là thanh ngang; BC là độ rộng giữa hai bên thang.
MN nằm chính giữa thang nên M; N là trung điểm AB và AC.
Suy ra MN là đường trung bình của tam giác ABC.
Suy ra MN = \(\frac{1}{2}BC = \frac{1}{2}.80 = 40\,\,(cm)\).
Vậy người thợ đã làm thanh ngang đó dài 40 cm.
a) Sử dụng công thức tính diện tích hình thang để suy ra đường cao ME.
b) Sử dụng hệ quả của định lí Thales để chứng minh.
c) Sử dụng hệ quả của định lí Thales để tính IF. Sử dụng công thức tính diện tích tam giác.
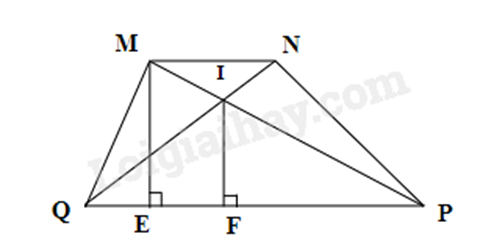
a) Ta có:
\(\begin{array}{l}{S_{MNPQ}} = \frac{1}{2}\left( {MN + PQ} \right).ME\\ \Rightarrow ME = \frac{{2{S_{MNPQ}}}}{{MN + PQ}} = \frac{{2.36}}{{4 + 8}} = 6\left( {cm} \right)\end{array}\)
b) Xét \(\Delta IPQ\) có MN // PQ nên \(\frac{{IP}}{{IM}} = \frac{{PQ}}{{MN}} \Rightarrow \frac{{IP}}{{IM}} = \frac{8}{4} = 2\) (hệ quả của định lí Thales)
\(\begin{array}{l} \Rightarrow \frac{{IP}}{{IP + IM}} = \frac{2}{{2 + 1}}\\ \Rightarrow \frac{{IP}}{{MP}} = \frac{2}{3}\end{array}\)
\( \Rightarrow IP = \frac{2}{3}MP\) (đpcm)
c) Kẻ \(IF \bot PQ\), mà \(ME \bot PQ\) \( \Rightarrow IF//ME\)
Do \(\Delta PME\) có \(IF//ME\) nên \(\frac{{IF}}{{ME}} = \frac{{IP}}{{MP}} = \frac{2}{3}\)
\( \Rightarrow IF = \frac{2}{3}ME \Rightarrow IF = \frac{2}{3}.6 = 4\left( {cm} \right)\)
\( \Rightarrow {S_{\Delta IPQ}} = \frac{{IF.PQ}}{2} = \frac{{4.8}}{2} = 16\left( {c{m^2}} \right)\)
Tìm điều kiện để hai đường thẳng cắt nhau.
Tìm tọa độ giao điểm 2 đường thẳng.
Tìm nghiệm nguyên.
Ta có: \(d \cap d'\) khi và chỉ khi \(m \ne 2\).
Xét phương trình hoành độ giao điểm của hai đường thẳng d và d’, ta có:
\(\begin{array}{l}mx - 2 = 2x + 1\\mx - 2x = 1 + 2\\\left( {m - 2} \right)x = 3\\x = \frac{3}{{m - 2}}\end{array}\)
Để hai đường thẳng d và d’ cắt nhau tại điểm có hoành độ là số nguyên thì \(x = \frac{3}{{m - 2}} \in \mathbb{Z}\) \( \Leftrightarrow 3 \vdots \left( {m - 2} \right)\) hay \(m - 3 \in \) Ư(3) \( = \left\{ { \pm 1; \pm 3} \right\}\).
Ta có bảng giá trị sau:

Vậy \(m \in \left\{ { - 1;1;3;5} \right\}\) thì hai đường thẳng d: y = mx -2; d’: y = 2x + 1 cắt nhau tại điểm có hoành độ là số nguyên.
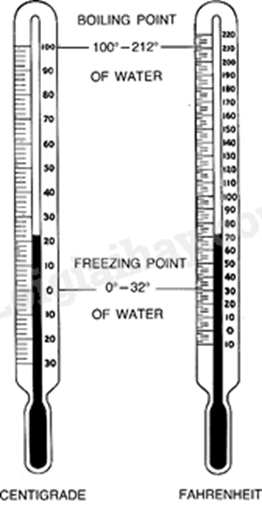 a) C có phải là hàm số bậc nhất theo biến số F không? Giải thích.
a) C có phải là hàm số bậc nhất theo biến số F không? Giải thích.
