Trắc nghiệm Bài 2: Ứng dụng của định lí Thalès trong tam giác Toán 8 Cánh diều
Đề bài
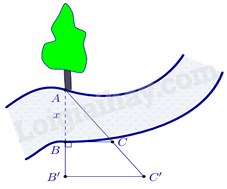
Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết \(BB' = 20\) m, \(BC = 30\) m và \(B'C = 40\) m. Tính độ rộng \(x\) của khúc sông.
-
A.
30m
-
B.
60m
-
C.
90m
-
D.
120m
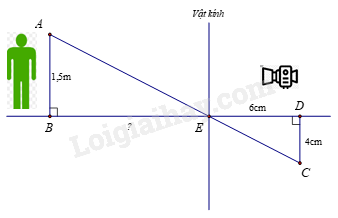
Người ta dùng máy ảnh để chụp một người có chiều cao \(AB = 1,5\) m (như hình vẽ). Sau khi rửa phim thấy ảnh \(CD\) cao 4cm. Biết khoảng cách từ phim đến vật kính của máy ảnh lúc chụp là \(ED = 6\) cm. Hỏi người đó đứng cách vật kính máy ảnh một đoạn \(BE\) bao nhiêu cm?
-
A.
150cm
-
B.
200cm
-
C.
225cm
-
D.
250cm
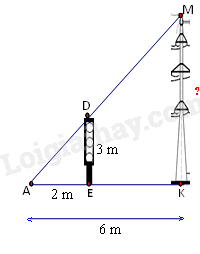
Bóng \(\left( {AK} \right)\) của một cột điện \(\left( {MK} \right)\) trên mặt đất dài 6m. Cùng lúc đó một cột đèn giao thông \(\left( {DE} \right)\) cao 3m có bóng \(\left( {AE} \right)\) dài 2m. Tính chiều cao của cột điện \(\left( {MK} \right)\) .
-
A.
6cm
-
B.
9cm
-
C.
12cm
-
D.
18cm
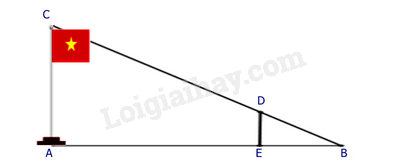
Để đo chiều cao \(AC\) của một cột cờ, người ta cắm một cái cọc \(ED\) có chiều cao 2m vuông góc với mặt đất. Đặt vị trí quan sát tại \(B\) , biết khoảng cách \(BE\) là 1,5m và khoảng cách \(AB\) là 9m.
Tính chiều cao \(AC\) của cột cờ.
-
A.
6m
-
B.
9m
-
C.
12m
-
D.
18m
Một cột đèn cao 10m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét).

-
A.
4,8mg
-
B.
6,8m
-
C.
7m
-
D.
10m
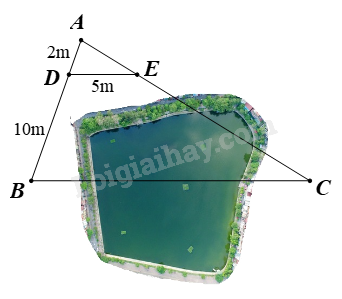
Giữa hai điểm \(B\) và \(C\) có một cái ao. Để đo khoảng cách \(BC\) người ta đo được các đoạn thẳng \(AD = 2\) , \(BD = 10\) m và \(DE = 5\) m. Biết \(DE // BC\) , tính khoảng cách giữa hai điểm \(B\) và \(C\) .
-
A.
12m
-
B.
30m
-
C.
25m
-
D.
13m
Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm?

-
A.
80cm
-
B.
40cm
-
C.
160cm
-
D.
120cm
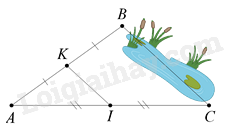
Giữa hai điểm \(B\) và \(C\) bị ngăn cách bởi hồ nước (như hình dưới) . Hãy xác định độ dài \(BC\) mà không cần phải bơi qua hồ. Biết rằng đoạn thẳng \(KI\) dài 25m và \(K\) là trung điểm của \(AB\) , \(I\) là trung điểm của \(AC\) .
-
A.
12,5m
-
B.
50m
-
C.
25m
-
D.
100m
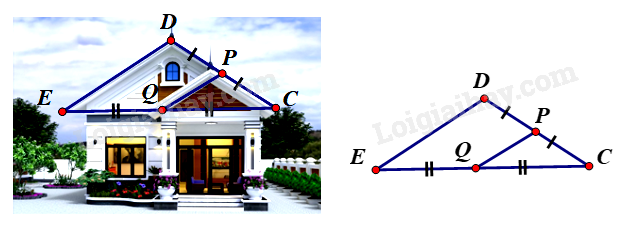
Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái \(PQ = 1,5\) m. Chú thợ nhẩm tính chiều dài mái \(DE\) biết \(Q\) là trung điểm \(EC\) , \(P\) là trung điểm của \(DC\) . Em hãy tính giúp chú thợ xem chiều dài mái \(DE\) bằng bao nhiêu (xem hình vẽ minh họa)?
-
A.
3m
-
B.
6m
-
C.
9m
-
D.
12m
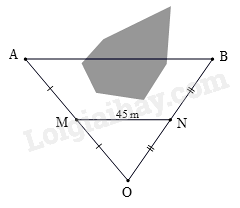
Để đo khoảng cách giữa hai điểm \(A\) và \(B\) bị ngăn cách bởi một hồ nước người ta đóng các cọc tại các vị trí \(A,\,B,\,M,\,N,\,O\) như hình bên và đo được \(MN = 45\) m. Tính khoảng cách \(AB\) biết \(M,\,N\) lần lượt là điểm chính giữa \(OA\) và \(OB\) .
-
A.
22,5m
-
B.
45m
-
C.
90m
-
D.
67,5m
Nhà tâm lý học Abraham Maslow (1908 – 1970) được xem như một trong những người tiên phong trong trường phái Tâm lý học nhân văn. Năm 1943, ông đã phát triển Lý thuyết về Thang bậc nhu cầu của con người (như hình vẽ bên). Trong đó, \(BK = 6\) cm. Hãy tính đoạn thẳng \(CJ;\,EH\) ?
-
A.
\(CJ = 6{\rm{cm}};\,EH = 12{\rm{cm}}\)
-
B.
\(CJ = 12{\rm{cm}};\,EH = 24{\rm{cm}}\)
-
C.
\(CJ = 9{\rm{cm}};\,EH = 18{\rm{cm}}\)
-
D.
\(CJ = 12{\rm{cm}};\,EH = 18{\rm{cm}}\)
Để làm cây thông noel, người thợ sẽ dùng một cái khung sắt hình tam giác cân như hình vẽ bên, sau đó gắn mô hình cây thông lên. Cho biết thanh \(BC = 120\) cm. Tính độ dài các thanh \(GF,\,HE,\,ID\) .

-
A.
\(GF = 30{\rm{cm}};\,HE = 60{\rm{cm}};\,ID = 90{\rm{cm}}\)
-
B.
\(GF = 30{\rm{cm}};\,HE = 60{\rm{cm}};\,ID = 120{\rm{cm}}\)
-
C.
\(GF = 30{\rm{cm}};\,HE = 90{\rm{cm}};\,ID = 120{\rm{cm}}\)
-
D.
\(GF = 60{\rm{cm}};\,HE = 90{\rm{cm}};\,ID = 120{\rm{cm}}\)
Lời giải và đáp án
Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết \(BB' = 20\) m, \(BC = 30\) m và \(B'C = 40\) m. Tính độ rộng \(x\) của khúc sông.

-
A.
30m
-
B.
60m
-
C.
90m
-
D.
120m
Đáp án : B
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Dùng hệ quả của định lý Thalès, ta có:
\(\frac{{AB}}{{AB'}} = \frac{{BC}}{{B'C'}} \Rightarrow \frac{x}{{x + 20}} = \frac{{30}}{{40}} \Rightarrow x = 60\) m.
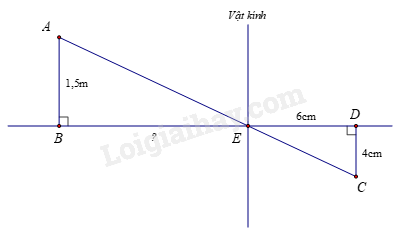
Người ta dùng máy ảnh để chụp một người có chiều cao \(AB = 1,5\) m (như hình vẽ). Sau khi rửa phim thấy ảnh \(CD\) cao 4cm. Biết khoảng cách từ phim đến vật kính của máy ảnh lúc chụp là \(ED = 6\) cm. Hỏi người đó đứng cách vật kính máy ảnh một đoạn \(BE\) bao nhiêu cm?

-
A.
150cm
-
B.
200cm
-
C.
225cm
-
D.
250cm
Đáp án : C
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Đổi đơn vị: 1,5m=150cm.
Ta có: \(AB // CD\) (cùng vuông góc với \(BD\) ) \( \Rightarrow \frac{{EB}}{{ED}} = \frac{{AB}}{{CD}}\) (hệ quả định lí Thalès)
\( \Rightarrow EB = \frac{{ED.AB}}{{CD}} = \frac{{6.150}}{4} = 225\) (cm)
Vậy người đứng cách vật kính máy ảnh là 225cm.
Bóng \(\left( {AK} \right)\) của một cột điện \(\left( {MK} \right)\) trên mặt đất dài 6m. Cùng lúc đó một cột đèn giao thông \(\left( {DE} \right)\) cao 3m có bóng \(\left( {AE} \right)\) dài 2m. Tính chiều cao của cột điện \(\left( {MK} \right)\) .

-
A.
6cm
-
B.
9cm
-
C.
12cm
-
D.
18cm
Đáp án : B
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Ta có : DE // MK
\( \Rightarrow \,\,\frac{{DE}}{{MK}} = \frac{{AE}}{{AK}}\)
\( \Leftrightarrow \,\,\frac{3}{{MK}} = \frac{2}{6}\)
\( \Rightarrow MK = \frac{{6.3}}{2} = 9\) (m)
Để đo chiều cao \(AC\) của một cột cờ, người ta cắm một cái cọc \(ED\) có chiều cao 2m vuông góc với mặt đất. Đặt vị trí quan sát tại \(B\) , biết khoảng cách \(BE\) là 1,5m và khoảng cách \(AB\) là 9m.
Tính chiều cao \(AC\) của cột cờ.

-
A.
6m
-
B.
9m
-
C.
12m
-
D.
18m
Đáp án : C
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Xét \(\Delta ABC\) có \(AC // ED\left( {AC \bot AB,\,ED \bot AB} \right)\)
\( \Rightarrow \frac{{EB}}{{AB}} = \frac{{ED}}{{AC}}\) (hệ quả của định lí Thalès)
\( \Leftrightarrow \frac{{1,5}}{9} = \frac{2}{{AC}}\)
\( \Rightarrow AC = 12\) (m)
Vậy chiều cao \(AC\) của cột cờ là 12m.
Một cột đèn cao 10m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét).

-
A.
4,8mg
-
B.
6,8m
-
C.
7m
-
D.
10m
Đáp án : C
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
\(MC = MA + AC = 4,8 + 2 = 6,8\) (m)
Xét \(\Delta DCM\) có \(AB // CD\) nên \(\frac{{AB}}{{CD}} = \frac{{MA}}{{MC}}\) (hệ quả định lí Thalès)
\( \Leftrightarrow \frac{{AB}}{{10}} = \frac{{4,8}}{{6,8}} \Rightarrow AB = \frac{{4,8.10}}{{6,8}} \approx 7\) (m)
Vậy chiều cao của cây xanh đó là 7m.
Giữa hai điểm \(B\) và \(C\) có một cái ao. Để đo khoảng cách \(BC\) người ta đo được các đoạn thẳng \(AD = 2\) , \(BD = 10\) m và \(DE = 5\) m. Biết \(DE // BC\) , tính khoảng cách giữa hai điểm \(B\) và \(C\) .

-
A.
12m
-
B.
30m
-
C.
25m
-
D.
13m
Đáp án : B
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Xét \(\Delta ABC\) có \(DE // BC\)
\( \Rightarrow \frac{{AD}}{{AB}} = \frac{{DE}}{{BC}}\)
\( \Leftrightarrow \frac{2}{{10 + 2}} = \frac{5}{{BC}}\)
\( \Rightarrow BC = \frac{{5\left( {10 + 2} \right)}}{2} = 30\) m
Vậy khoảng cách giữa hai điểm \(B\) và \(C\) là 30m.
Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm?

-
A.
80cm
-
B.
40cm
-
C.
160cm
-
D.
120cm
Đáp án : B
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Sử dụng định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
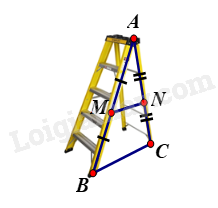
Gọi \(MN\) là thanh ngang; \(BC\) là độ rộng giữa hai bên thang.
\(MN\) nằm chính giữa thang nên \(M,\,N\) là trung điểm \(AB\) và \(AC\) .
\( \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2}\)
\( \Rightarrow MN // BC\) (định lí Thalès đảo)
\( \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (hệ quả định lí Thalès)
\( \Rightarrow MN = \frac{1}{2}BC = \frac{1}{2} \cdot 80 = 40\) (cm)
Vậy người thợ đã làm thanh ngang đó dài 40cm.
Giữa hai điểm \(B\) và \(C\) bị ngăn cách bởi hồ nước (như hình dưới) . Hãy xác định độ dài \(BC\) mà không cần phải bơi qua hồ. Biết rằng đoạn thẳng \(KI\) dài 25m và \(K\) là trung điểm của \(AB\) , \(I\) là trung điểm của \(AC\) .

-
A.
12,5m
-
B.
50m
-
C.
25m
-
D.
100m
Đáp án : B
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Sử dụng định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Xét \(\Delta ABC\) có: \(K\) là trung điểm của \(AB\) , \(I\) là trung điểm của \(AC\)
\( \Rightarrow \frac{{AK}}{{AB}} = \frac{{AI}}{{AC}} = \frac{1}{2}\)
\( \Rightarrow KI // BC\) (định lí Thalès đảo)
\( \Rightarrow \frac{{AK}}{{AB}} = \frac{{AI}}{{AC}} = \frac{{KI}}{{BC}}\) (hệ quả định lí Thalès)
\( \Rightarrow BC = 2KI = 2.25 = 50\) (m)
Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái \(PQ = 1,5\) m. Chú thợ nhẩm tính chiều dài mái \(DE\) biết \(Q\) là trung điểm \(EC\) , \(P\) là trung điểm của \(DC\) . Em hãy tính giúp chú thợ xem chiều dài mái \(DE\) bằng bao nhiêu (xem hình vẽ minh họa)?

-
A.
3m
-
B.
6m
-
C.
9m
-
D.
12m
Đáp án : A
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Sử dụng định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Vì \(Q\) là trung điểm \(EC\) , \(P\) là trung điểm của \(DC\) nên
\(\frac{{CQ}}{{CE}} = \frac{{CP}}{{CD}} = \frac{1}{2}\)
\( \Rightarrow QP // ED\) (định lí Thalès đảo)
\( \Rightarrow \frac{{CQ}}{{CE}} = \frac{{CP}}{{CD}} = \frac{{QP}}{{ED}}\) (hệ quả định lí Thalès)
\( \Rightarrow DE = 2PQ = 2.1,5 = 3\) (m)
Vậy chiều dài mái \(DE\) bằng 3m.
Để đo khoảng cách giữa hai điểm \(A\) và \(B\) bị ngăn cách bởi một hồ nước người ta đóng các cọc tại các vị trí \(A,\,B,\,M,\,N,\,O\) như hình bên và đo được \(MN = 45\) m. Tính khoảng cách \(AB\) biết \(M,\,N\) lần lượt là điểm chính giữa \(OA\) và \(OB\) .

-
A.
22,5m
-
B.
45m
-
C.
90m
-
D.
67,5m
Đáp án : C
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Sử dụng định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
\(M,\,N\) lần lượt là điểm chính giữa \(OA\) và \(OB\) .
\( \Rightarrow \frac{{OM}}{{OA}} = \frac{1}{2};\frac{{ON}}{{OB}} = \frac{1}{2} \Rightarrow \frac{{OM}}{{OA}} = \frac{{ON}}{{OB}} \Rightarrow MN // AB\) (định lí Thalès đảo)
\( \Rightarrow \frac{{OM}}{{OA}} = \frac{{ON}}{{OB}} = \frac{{MN}}{{AB}}\) (hệ quả định lí Thalès)
\( \Rightarrow AB = 2MN = 2.45 = 90\) m.
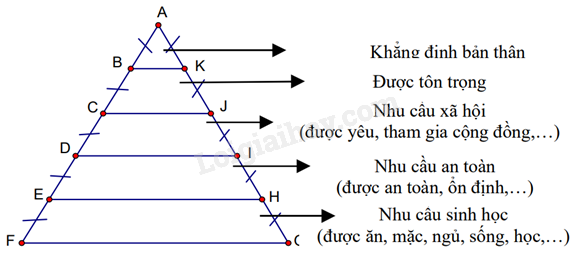
Nhà tâm lý học Abraham Maslow (1908 – 1970) được xem như một trong những người tiên phong trong trường phái Tâm lý học nhân văn. Năm 1943, ông đã phát triển Lý thuyết về Thang bậc nhu cầu của con người (như hình vẽ bên). Trong đó, \(BK = 6\) cm. Hãy tính đoạn thẳng \(CJ;\,EH\) ?

-
A.
\(CJ = 6{\rm{cm}};\,EH = 12{\rm{cm}}\)
-
B.
\(CJ = 12{\rm{cm}};\,EH = 24{\rm{cm}}\)
-
C.
\(CJ = 9{\rm{cm}};\,EH = 18{\rm{cm}}\)
-
D.
\(CJ = 12{\rm{cm}};\,EH = 18{\rm{cm}}\)
Đáp án : B
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Sử dụng định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Ta có: \(AB = BC = CD = DE = EF = \frac{{AF}}{5}\) ;
\(AK = KJ = JI = IH = HO = \frac{{AO}}{5}\)
\(\left. \begin{array}{l}AC = AB + BC = 2AB \Rightarrow \frac{{AB}}{{AC}} = \frac{1}{2}\\AJ = AK + KJ = 2AK \Rightarrow \frac{{AK}}{{AJ}} = \frac{1}{2}\end{array} \right\} \Rightarrow \frac{{AB}}{{AC}} = \frac{{AK}}{{AJ}}\)
\( \Rightarrow BK // CJ\) (định lí Thalès đảo)
\( \Rightarrow \frac{{AB}}{{AC}} = \frac{{AK}}{{AJ}} = \frac{{BK}}{{CJ}}\) (hệ quả định lí Thalès)
\( \Rightarrow CJ = 2BK = 2.6 = 12\) cm
\(\left. \begin{array}{l}AE = AB + BC + CD + DE = 4AB \Rightarrow \frac{{AC}}{{AE}} = \frac{{2AB}}{{4AB}} = \frac{1}{2}\\AH = AK + KJ + JI + IH = 4AK \Rightarrow \frac{{AJ}}{{AH}} = \frac{{2AK}}{{4AK}} = \frac{1}{2}\end{array} \right\} \Rightarrow \frac{{AC}}{{AE}} = \frac{{AJ}}{{AH}}\)
\( \Rightarrow CJ // EH\) (định lí Thalès đảo)
\( \Rightarrow \frac{{AC}}{{AE}} = \frac{{AJ}}{{AH}} = \frac{{CJ}}{{EH}}\) (hệ quả định lí Thalès)
\( \Rightarrow EH = 2CJ = 2.12 = 24\) cm
Để làm cây thông noel, người thợ sẽ dùng một cái khung sắt hình tam giác cân như hình vẽ bên, sau đó gắn mô hình cây thông lên. Cho biết thanh \(BC = 120\) cm. Tính độ dài các thanh \(GF,\,HE,\,ID\) .

-
A.
\(GF = 30{\rm{cm}};\,HE = 60{\rm{cm}};\,ID = 90{\rm{cm}}\)
-
B.
\(GF = 30{\rm{cm}};\,HE = 60{\rm{cm}};\,ID = 120{\rm{cm}}\)
-
C.
\(GF = 30{\rm{cm}};\,HE = 90{\rm{cm}};\,ID = 120{\rm{cm}}\)
-
D.
\(GF = 60{\rm{cm}};\,HE = 90{\rm{cm}};\,ID = 120{\rm{cm}}\)
Đáp án : A
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Sử dụng định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Ta có: \(AG = GH = HI = IB = \frac{{AB}}{4};\,AF = FE = ED = DC = \frac{{AC}}{4}\)
Xét \(\Delta ABC\) có \(\frac{{AG}}{{AB}} = \frac{{AF}}{{AC}} = \frac{1}{4}\)
\( \Rightarrow GF // BC\) (định lí Thalès đảo)
\( \Rightarrow \frac{{AG}}{{AB}} = \frac{{AF}}{{AC}} = \frac{{GF}}{{BC}}\) (hệ quả định lí Thalès)
\( \Rightarrow GF = \frac{{BC}}{4} = \frac{{120}}{4} = 30\) (cm)
\(\left. \begin{array}{l}\frac{{AG}}{{AH}} = \frac{{AG}}{{AG + GH}} = \frac{{AG}}{{2AG}} = \frac{1}{2}\\\frac{{AF}}{{AE}} = \frac{{AF}}{{AF + FE}} = \frac{{AF}}{{2AF}} = \frac{1}{2}\end{array} \right\} \Rightarrow \frac{{AG}}{{AH}} = \frac{{AF}}{{AE}} = \frac{1}{2} \Rightarrow GF // HE\) (định lí Thalès đảo)
\( \Rightarrow \frac{{AG}}{{AH}} = \frac{{AF}}{{AE}} = \frac{{GF}}{{HE}}\) (hệ quả định lí Thalès)
\( \Rightarrow HE = 2GF = 2.30 = 60\) (cm)
\(\left. \begin{array}{l}\frac{{AG}}{{AI}} = \frac{{AG}}{{AG + GH + HI}} = \frac{{AG}}{{3AG}} = \frac{1}{3}\\\frac{{AF}}{{AD}} = \frac{{AF}}{{AF + FE + ED}} = \frac{{AF}}{{3AF}} = \frac{1}{3}\end{array} \right\} \Rightarrow \frac{{AG}}{{AI}} = \frac{{AF}}{{AD}} = \frac{1}{3}\)
\( \Rightarrow GF // ID\) (định lí Thalès đảo)
\( \Rightarrow \frac{{AG}}{{AI}} = \frac{{AF}}{{AD}} = \frac{{GF}}{{ID}}\) (hệ quả định lí Thalès)
\( \Rightarrow ID = 3GF = 3.30 = 90\) (cm)