Đề thi giữa kì 1 Toán 12 - Đề số 8
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số đồng biến trên khoảng
-
A.
\(( - 1;1)\)
-
B.
\(( - \infty ; - 2)\)
-
C.
\((1; + \infty )\)
-
D.
\(( - 2;1)\)
-
A.
\(y = {x^3} - 3{x^2} - 1\)
-
B.
\(y = - {x^4} + 2{x^2} - 1\)
-
C.
\(y = {x^4} - 2{x^2} - 1\)
-
D.
\(y = - {x^3} + 3{x^2} - 1\)
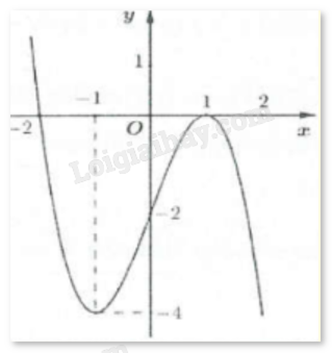
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
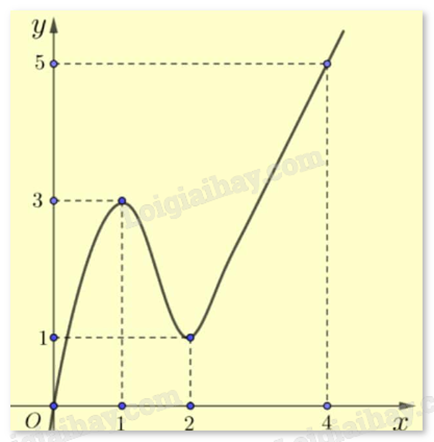
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;2]. Tính M - m.
-
A.
1
-
B.
2
-
C.
3
-
D.
4
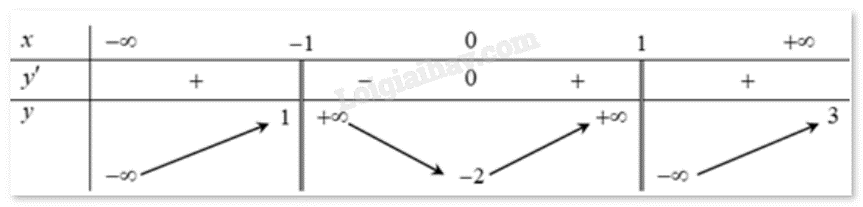
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
-
A.
1
-
B.
4
-
C.
2
-
D.
3
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 1}}{x}\) là:
-
A.
\(y = x + 2\)
-
B.
\(y = - x - 2\)
-
C.
\(y = 2x\)
-
D.
\(y = 2\)
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{3x - 7}}{{x + 2}}\) là:
-
A.
(3;-2)
-
B.
(-2;3)
-
C.
(2;-3)
-
D.
(-3;2)
Trong các mệnh đề sau, mệnh đề nào sai?
-
A.
Vì I là trung điểm đoạn AB nên từ O bất kì ta có: \(\overrightarrow {OI} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
-
B.
Vì \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \) nên bốn điểm A, B, C, D đồng phẳng
-
C.
Vì \(\overrightarrow {NM} + \overrightarrow {NP} = \overrightarrow 0 \) nên N là trung điểm của đoạn NP
-
D.
Từ hệ thức \(\overrightarrow {AB} = 2\overrightarrow {AC} - 8\overrightarrow {AD} \) ta suy ra ba vecto \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) đồng phẳng
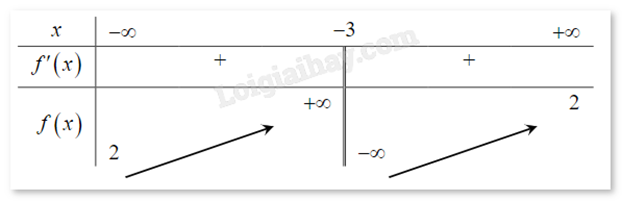
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có bảng biến thiên như hình vẽ bên. Hỏi hàm số đã cho là hàm số nào?
-
A.
\(y = \frac{{2x + 1}}{{x - 3}}\)
-
B.
\(y = \frac{{2 - x}}{{x + 3}}\)
-
C.
\(y = \frac{{2x + 7}}{{x + 3}}\)
-
D.
\(y = \frac{{2x - 1}}{{x + 3}}\)
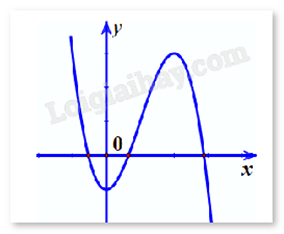
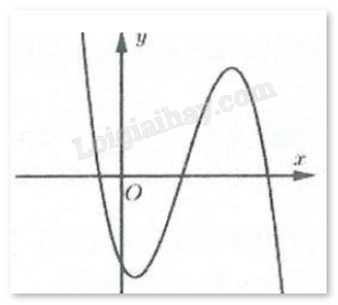
Đường cong hình bên là đồ thị của hàm số \(y = a{x^3} + b{x^2} + cx + d\). Khẳng định nào sau đây đúng?
-
A.
a < 0, b < 0, c > 0, d < 0
-
B.
a > 0, b > 0, c < 0, d < 0
-
C.
a < 0, b < 0, c < 0, d > 0
-
D.
a < 0, b > 0, c < 0, d < 0
Cho hàm số y = f(x) xác định và liên tục trên R và có đô thị của đạo hàm y = f’(x) như hình bên dưới. Chọn phát biểu đúng khi nói về hàm số y = f(x).
-
A.
Hàm số y = f(x) có hai điểm cực trị
-
B.
Hàm số nghịch biến trên khoảng (-3;0)
-
C.
f(0) > f(3)
-
D.
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \) và \(\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty \)
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
-
A.
\({90^o}\)
-
B.
\({60^o}\)
-
C.
\({45^o}\)
-
D.
\({120^o}\)
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 4\), \(\left| {\overrightarrow b } \right| = 3\), \(\left| {\overrightarrow a - \overrightarrow b } \right| = 4\). Gọi \(\alpha \) là góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \). Chọn khẳng định đúng?
-
A.
\(\cos \alpha = \frac{3}{8}\)
-
B.
\(\alpha = {30^o}\)
-
C.
\(\cos \alpha = \frac{1}{3}\)
-
D.
\(\alpha = {60^o}\)
a) Đồ thị hàm số đã cho có hai cực trị
b) Hàm số đã cho đồng biến trên R
c) Hàm số không có giá trị lớn nhất và nhỏ nhất
d) Đồ thị hàm số f(x) là \(y = \frac{{2{x^2} - 1}}{{x + 1}}\)
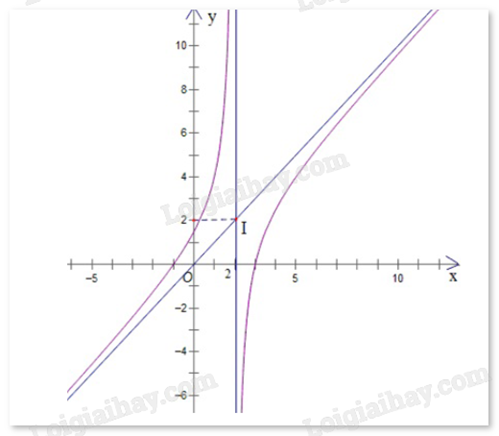
a) Đồ thị hàm số f(x) là đồ thị của hàm số \(y = \frac{{{x^2} - 2x - 3}}{{x - 1}}\)
b) Đồ thị hàm số nhận giao điểm I(2;2) của hai đường tiệm cận làm tâm đối xứng
c) Hàm số f(x) đồng biến trên mỗi khoảng \(( - \infty ;2)\) và \((2; + \infty )\)
d) Hàm số y = f(x) có hai cực trị
Cho hình hộp ABCD.A’B’C’D’ tâm O.
a) \(\overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AD} + \overrightarrow {DD'} \)
b) \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \)
c) \(\overrightarrow {AB} + \overrightarrow {BC'} + \overrightarrow {CD} + \overrightarrow {D'A} = \overrightarrow 0 \)
d) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC'} = \overrightarrow {AD'} + \overrightarrow {D'O} + \overrightarrow {OC'} \)
Trong không gian Oxyz, biết \(\overrightarrow c = (x;y;z)\) vuông góc vối cả hai vecto \(\overrightarrow a = (1;3;4)\), \(\overrightarrow b = ( - 1;2;3)\).
a) \(\overrightarrow a .\overrightarrow b = 15\)
b) \(\left| {\overrightarrow a } \right| = 5\)
c) \({\overrightarrow b ^2} = 14\)
d) \(7x + y = 0\)
Tìm giá trị nhỏ nhất của hàm số \(2{\cos ^3}x - \frac{9}{2}{\cos ^2}x + 3\cos x + \frac{1}{2}\).
Đáp án:
Với giá trị nào của tham số m để đồ thị hàm số \(y = \frac{{3x - 1}}{{2x - m}}\) có tiệm cận đứng đi qua điểm A(1;3)?
Đáp án:
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có A(-3;0;0), B(0;2;0), D(0;0;1), A’(1;2;3). Tính tổng của hoành độ, tung độ, cao độ đỉnh C’.
Đáp án:
Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300 km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc của cá bơi khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức \(E(v) = c{v^3}t\), trong đó c là một hằng số, E được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
Đáp án:
Giả sử một công ty du lịch bán tour với giá là x /khách thì doanh thu sẽ được biểu diễn qua hàm số \(f(x) = - 200{x^2} + 550x\). Công ty phải bán giá tour cho một khách là bao nhiêu (đơn vị: triệu đồng) để doanh thu từ tua xuyên Việt là lớn nhất (kết quả làm tròn đến hàng phần trăm)?
Đáp án:
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \((a,b,c,d \in \mathbb{R})\) có đồ thị như hình:

Có bao nhiêu số dương trong các số a, b, c, d?
Đáp án:
Lời giải và đáp án
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số đồng biến trên khoảng

-
A.
\(( - 1;1)\)
-
B.
\(( - \infty ; - 2)\)
-
C.
\((1; + \infty )\)
-
D.
\(( - 2;1)\)
Đáp án : A
Quan sát đồ thị và nhận xét.
Nhìn vào đồ thị ta thấy đồ thị hàm số đã cho đồng biến trên khoảng (-1;1); nghịch biến trên khoảng (-∞;-1) và (1;+∞).
-
A.
\(y = {x^3} - 3{x^2} - 1\)
-
B.
\(y = - {x^4} + 2{x^2} - 1\)
-
C.
\(y = {x^4} - 2{x^2} - 1\)
-
D.
\(y = - {x^3} + 3{x^2} - 1\)
Đáp án : D
Quan sát đồ thị và nhận xét.
Ta có đây là đồ thị hàm số bậc 3 dạng \(y = a{x^3} + b{x^2} + cx + d\) vì có 2 điểm cực trị, hệ số a < 0 (vì nhánh cuối đồ thị đi xuống).
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;2]. Tính M - m.
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : C
Quan sát đồ thị và nhận xét.
Dựa vào đồ thị ta thấy:
\(\mathop {\max }\limits_{[0;2]} f(x) = f(1) = 3\), \(\mathop {\min }\limits_{[0;2]} f(x) = f(0) = 0\). Vậy M – m = 3 – 0 = 3.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?

-
A.
1
-
B.
4
-
C.
2
-
D.
3
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Dựa vào bảng biến thiên ta có: \(\mathop {\lim }\limits_{x \to {{( - 1)}^ + }} f(x) = + \infty \), \(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = + \infty \) nên x = -1, x = 1 là tiệm cận đứng của đồ thị hàm số.
Mặt khác: \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 3\) nên y = 3 là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị có 3 tiệm cận.
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 1}}{x}\) là:
-
A.
\(y = x + 2\)
-
B.
\(y = - x - 2\)
-
C.
\(y = 2x\)
-
D.
\(y = 2\)
Đáp án : A
Thực hiện phép chia đa thức (ở tử) cho đa thức (ở mẫu) ta được \(y = ax + b + \frac{M}{{cx + d}}\)(a≠0) với M là hằng số.
Đường thẳng y = ax + b (a≠0) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
Kết luận đường thẳng y = ax +b là đường tiệm cận xiên của đồ thị hàm số.
Ta có: \(y = \frac{{{x^2} + 2x - 1}}{x} = x + 2 - \frac{1}{x} = f(x)\).
Từ đó: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - \left( {x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{x} = 0\).
Vậy đường thẳng \(y = x + 2\) là đường tiệm cận xiên của đồ thị hàm số đã cho.
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{3x - 7}}{{x + 2}}\) là:
-
A.
(3;-2)
-
B.
(-2;3)
-
C.
(2;-3)
-
D.
(-3;2)
Đáp án : B
Tâm đối xứng của đồ thị là giao điểm của các đường tiệm cận.
Đồ thị hàm số có tiệm cận đứng x = -2 và tiệm cận ngang y = 3, suy ra tâm đối xứng là giao điểm của hai tiệm cận có tọa độ (-2;3).
Trong các mệnh đề sau, mệnh đề nào sai?
-
A.
Vì I là trung điểm đoạn AB nên từ O bất kì ta có: \(\overrightarrow {OI} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
-
B.
Vì \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \) nên bốn điểm A, B, C, D đồng phẳng
-
C.
Vì \(\overrightarrow {NM} + \overrightarrow {NP} = \overrightarrow 0 \) nên N là trung điểm của đoạn NP
-
D.
Từ hệ thức \(\overrightarrow {AB} = 2\overrightarrow {AC} - 8\overrightarrow {AD} \) ta suy ra ba vecto \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) đồng phẳng
Đáp án : B
Dựa vào lý thuyết vecto cùng phương, vecto đồng phẳng, quy tắc trung điểm.
Câu B sai vì \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \) đúng với mọi điểm A, B, C, D.
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có bảng biến thiên như hình vẽ bên. Hỏi hàm số đã cho là hàm số nào?

-
A.
\(y = \frac{{2x + 1}}{{x - 3}}\)
-
B.
\(y = \frac{{2 - x}}{{x + 3}}\)
-
C.
\(y = \frac{{2x + 7}}{{x + 3}}\)
-
D.
\(y = \frac{{2x - 1}}{{x + 3}}\)
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Dựa vào bảng biến thiên ta thấy đồ thị nhận x = -3 là tiệm cận đứng và y = 2 là tiệm cận ngang. Loại A, B.
Hàm số đồng biến trên mỗi khoảng xác định.
Xét hàm số \(y = \frac{{2x + 7}}{{x + 3}} \Rightarrow y' = \frac{{ - 1}}{{{{(x + 3)}^2}}} < 0\) \((\forall x \ne - 3)\), ta loại đáp án C.
Đường cong hình bên là đồ thị của hàm số \(y = a{x^3} + b{x^2} + cx + d\). Khẳng định nào sau đây đúng?

-
A.
a < 0, b < 0, c > 0, d < 0
-
B.
a > 0, b > 0, c < 0, d < 0
-
C.
a < 0, b < 0, c < 0, d > 0
-
D.
a < 0, b > 0, c < 0, d < 0
Đáp án : D
Dựa vào sự biến thiên và cực trị của hàm số để xét dấu.
Dựa vào đồ thị ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) nên a < 0. Loại B.
Đồ thị đi qua điểm (0;d) nên d < 0 (vì đồ thị cắt trục tung tại điểm có tung độ âm).
Hàm số đạt cực trị tại hai điểm \({x_1},{x_2}\). Dựa vào hình vẽ ta thấy \({x_1} > 0,x{}_2 > 0\).
Mặt khác, \(y' = 3a{x^2} + 2bx + c \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = \frac{{ - 2b}}{{3a}} > 0 \Rightarrow b > 0}\\{{x_1}{x_2} = \frac{c}{{3a}} > 0 \Rightarrow c < 0}\end{array}} \right.\)
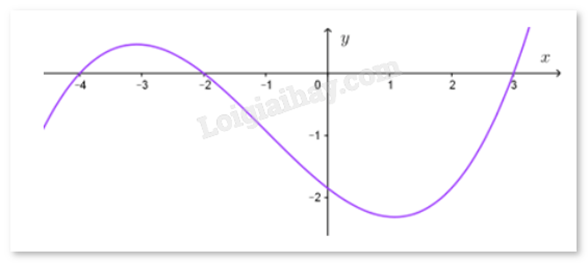
Cho hàm số y = f(x) xác định và liên tục trên R và có đô thị của đạo hàm y = f’(x) như hình bên dưới. Chọn phát biểu đúng khi nói về hàm số y = f(x).

-
A.
Hàm số y = f(x) có hai điểm cực trị
-
B.
Hàm số nghịch biến trên khoảng (-3;0)
-
C.
f(0) > f(3)
-
D.
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \) và \(\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty \)
Đáp án : C
Dựa vào sự biến thiên, cực trị, giới hạn thông qua đồ thị f’(x).
Ta thấy trên khoảng (0;3), f’(x) mang dấu âm nên hàm số nghịch biến trên (0;3). Suy ra f(0) > f(3).
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
-
A.
\({90^o}\)
-
B.
\({60^o}\)
-
C.
\({45^o}\)
-
D.
\({120^o}\)
Đáp án : C
Đưa về hai vecto chung gốc để xác định góc.
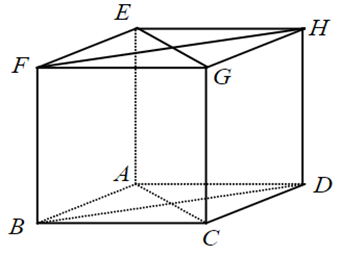
Ta có: EG//AC (do ACGE là hình bình hành), suy ra \(\left( {\overrightarrow {AB} ,\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = {45^o}\).
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 4\), \(\left| {\overrightarrow b } \right| = 3\), \(\left| {\overrightarrow a - \overrightarrow b } \right| = 4\). Gọi \(\alpha \) là góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \). Chọn khẳng định đúng?
-
A.
\(\cos \alpha = \frac{3}{8}\)
-
B.
\(\alpha = {30^o}\)
-
C.
\(\cos \alpha = \frac{1}{3}\)
-
D.
\(\alpha = {60^o}\)
Đáp án : A
Sử dụng công thức tính tích góc giữa hai vecto.
\({\left( {\overrightarrow a - \overrightarrow b } \right)^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} - 2\overrightarrow a .\overrightarrow b \Rightarrow \overrightarrow a .\overrightarrow b = \frac{9}{2}\).
Do đó: \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{3}{8}\).
a) Đồ thị hàm số đã cho có hai cực trị
b) Hàm số đã cho đồng biến trên R
c) Hàm số không có giá trị lớn nhất và nhỏ nhất
d) Đồ thị hàm số f(x) là \(y = \frac{{2{x^2} - 1}}{{x + 1}}\)
a) Đồ thị hàm số đã cho có hai cực trị
b) Hàm số đã cho đồng biến trên R
c) Hàm số không có giá trị lớn nhất và nhỏ nhất
d) Đồ thị hàm số f(x) là \(y = \frac{{2{x^2} - 1}}{{x + 1}}\)
Quan sát đồ thị và nhận xét.
a) Đúng . Hàm số f(x) có hai cực trị.
b) Sai. Hàm số có khoảng nghịch biến.
c) Đúng. Hàm số không có giá trị lớn nhất và nhỏ nhất.
d) Sai. Đồ thị có dạng của hàm số bậc 3.
a) Đồ thị hàm số f(x) là đồ thị của hàm số \(y = \frac{{{x^2} - 2x - 3}}{{x - 1}}\)
b) Đồ thị hàm số nhận giao điểm I(2;2) của hai đường tiệm cận làm tâm đối xứng
c) Hàm số f(x) đồng biến trên mỗi khoảng \(( - \infty ;2)\) và \((2; + \infty )\)
d) Hàm số y = f(x) có hai cực trị
a) Đồ thị hàm số f(x) là đồ thị của hàm số \(y = \frac{{{x^2} - 2x - 3}}{{x - 1}}\)
b) Đồ thị hàm số nhận giao điểm I(2;2) của hai đường tiệm cận làm tâm đối xứng
c) Hàm số f(x) đồng biến trên mỗi khoảng \(( - \infty ;2)\) và \((2; + \infty )\)
d) Hàm số y = f(x) có hai cực trị
Quan sát đồ thị và nhận xét.
a) Sai. Đồ thị \(y = \frac{{{x^2} - 2x - 3}}{{x - 1}}\) có tiệm cận đứng là x = 1. Tiệm cận đứng của đồ thị trên hinh là x = 2.
b) Đúng. Đồ thị hàm số nhận giao điểm I(2;2) của hai đường tiệm cận làm tâm đối xứng.
c) Đúng. Hàm số f(x) đồng biến trên mỗi khoảng \(( - \infty ;2)\) và \((2; + \infty )\).
d) Sai. Hàm số không có cực trị.
Cho hình hộp ABCD.A’B’C’D’ tâm O.
a) \(\overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AD} + \overrightarrow {DD'} \)
b) \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \)
c) \(\overrightarrow {AB} + \overrightarrow {BC'} + \overrightarrow {CD} + \overrightarrow {D'A} = \overrightarrow 0 \)
d) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC'} = \overrightarrow {AD'} + \overrightarrow {D'O} + \overrightarrow {OC'} \)
a) \(\overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AD} + \overrightarrow {DD'} \)
b) \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \)
c) \(\overrightarrow {AB} + \overrightarrow {BC'} + \overrightarrow {CD} + \overrightarrow {D'A} = \overrightarrow 0 \)
d) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC'} = \overrightarrow {AD'} + \overrightarrow {D'O} + \overrightarrow {OC'} \)
Sử dụng quy tắc cộng vecto, lý thuyết các vecto bằng nhau, vecto đối nhau, quy tắc ba điểm, quy tắc hình hộp.
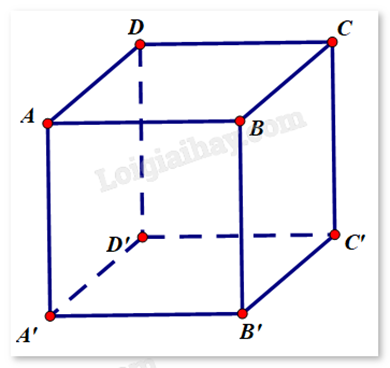
a) Sai . \(\overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AB'} \), \(\overrightarrow {AD} + \overrightarrow {DD'} = \overrightarrow {AD'} \), mà \(\overrightarrow {AB'} \ne \overrightarrow {AD'} \) nên \(\overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AD} + \overrightarrow {DD'} \) sai.
b) Đúng. Theo quy tắc hình hộp: \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
c) Đúng . \((\overrightarrow {AB} + \overrightarrow {CD} ) + (\overrightarrow {BC'} + \overrightarrow {D'A} ) = \overrightarrow 0 \Leftrightarrow \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \).
d) Đúng. \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC'} = \overrightarrow {AC'} \), \(\overrightarrow {AD'} + \overrightarrow {D'O} + \overrightarrow {OC'} = \overrightarrow {AC'} \), suy ra \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC'} = \overrightarrow {AD'} + \overrightarrow {D'O} + \overrightarrow {OC'} \).
Trong không gian Oxyz, biết \(\overrightarrow c = (x;y;z)\) vuông góc vối cả hai vecto \(\overrightarrow a = (1;3;4)\), \(\overrightarrow b = ( - 1;2;3)\).
a) \(\overrightarrow a .\overrightarrow b = 15\)
b) \(\left| {\overrightarrow a } \right| = 5\)
c) \({\overrightarrow b ^2} = 14\)
d) \(7x + y = 0\)
a) \(\overrightarrow a .\overrightarrow b = 15\)
b) \(\left| {\overrightarrow a } \right| = 5\)
c) \({\overrightarrow b ^2} = 14\)
d) \(7x + y = 0\)
Sử dụng các quy tắc cộng vecto, công thức tính tích vô hướng của hai vecto, độ dài vecto.
a) Sai . Vì \(\overrightarrow a .\overrightarrow b = 1.( - 1) + 3.2 + 4.3 = 17\).
b) Sai . Vì \(\left| {\overrightarrow a } \right| = \sqrt {{1^2} + {3^2} + {4^2}} = \sqrt {26} \).
c) Đúng . Vì \({\overrightarrow b ^2} = {\left| {\overrightarrow b } \right|^2} = {( - 1)^2} + {2^2} + {3^3} = 14\) .
d) Đúng . Theo giả thiết ta có \(\overrightarrow c = (x;y;z) \ne \overrightarrow 0 \) và vuông góc với cả hai vecto \(\overrightarrow a = (1;3;4)\) và \(\overrightarrow b = ( - 1;2;3)\) nên \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow c .\overrightarrow a = 0}\\{\overrightarrow c .\overrightarrow b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1x + 3y + 4z = 0}\\{ - 1x + 2y + 3z = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1x + 3y + 4z = 0}\\{5y + 7z = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1x + 3y + 4\frac{{ - 5}}{7}y = 0}\\{z = \frac{{ - 5}}{7}y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{7x + y = 0}\\{5y + 7z = 0}\end{array}} \right.\)
Tìm giá trị nhỏ nhất của hàm số \(2{\cos ^3}x - \frac{9}{2}{\cos ^2}x + 3\cos x + \frac{1}{2}\).
Đáp án:
Đáp án:
- Tính y’, tìm các nghiệm của y’ = 0.
- Tìm giá trị y tại các điểm cực trị của hàm số và hai đầu mút của đoạn.
Đặt \(t = \cos x \in [ - 1;1]\), khi đó \(y = f(t) = 2{t^3} - \frac{9}{2}{t^2} + 3t + \frac{1}{2}\).
Ta có: \(f'(t) = 8{t^2} - 9t + 3 > 0\) \(\forall t\).
Suy ra hàm f(t) đồng biến trên (-1;1), do đó giá trị nhỏ nhất của hàm số là f(-1) = 1.
Với giá trị nào của tham số m để đồ thị hàm số \(y = \frac{{3x - 1}}{{2x - m}}\) có tiệm cận đứng đi qua điểm A(1;3)?
Đáp án:
Đáp án:
Sử dụng quy tắc tìm đường tiệm cận của hàm phân thức.
Tiệm cận đứng của đồ thị hàm số là \(x = \frac{m}{2}\).
Tiệm cận đứng của đồ thị hàm số đi qua điểm A(1;3) nên \(\frac{m}{2} = 1 \Leftrightarrow m = 2\).
Thử lại thấy thỏa mãn.
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có A(-3;0;0), B(0;2;0), D(0;0;1), A’(1;2;3). Tính tổng của hoành độ, tung độ, cao độ đỉnh C’.
Đáp án:
Đáp án:
Sử dụng quy tắc hình hộp.
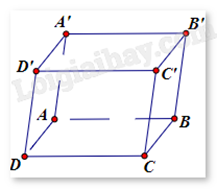
Gọi C’(x;y;z). Ta có: \(\overrightarrow {AB} = (3;2;0)\), \(\overrightarrow {AD} = (3;0;1)\), \(\overrightarrow {AA'} = (4;2;3)\).
Mà \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \), suy ra \(\overrightarrow {AC'} = (10;4;4)\).
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{x = 10 + 3}\\{y = 4 - 0}\\{z = 4 - 0}\end{array}} \right.\), vậy C’(13;4;4).
Vậy tổng cần tìm là 13 + 4 + 4 = 21.
Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300 km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc của cá bơi khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức \(E(v) = c{v^3}t\), trong đó c là một hằng số, E được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
Đáp án:
Đáp án:
Thiết lập hàm số tính năng lượng với thời gian t khi cá bơi ngược dòng. Lập bảng biến thiên và tìm giá trị lớn nhất của hàm số.
Vận tốc cá bơi khi ngược dòng là v – 6 (km/h). Thời gian cá bơi để vượt khoảng cách 300 km là \(t = \frac{{300}}{{v - 6}}\) (giờ).
Năng lương tiêu hao của cá để vượt khoảng cách đó là \(E(v) = c{v^3}.\frac{{300}}{{v - 6}} = 300c.\frac{{{v^3}}}{{v - 6}}\) (jun), v > 6.
Ta có: \(E'(v) = 600c{v^2}\frac{{v - 9}}{{{{(v - 6)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{{20}{c}}{v = 0}\\{v = 9}\end{array}} \right.\)
Loại v = 0 vì v > 6.
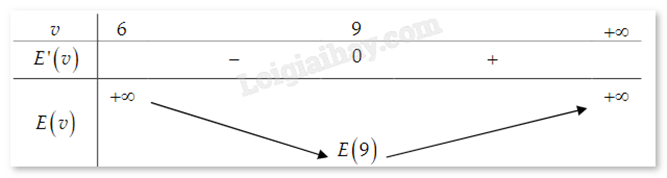
Dựa vào bảng biến thiên, ta thấy để tiêu hao ít năng lượng nhất, cá phải bơi với vận tốc (khi nước đứng yên) là 9 (km/h).
Giả sử một công ty du lịch bán tour với giá là x /khách thì doanh thu sẽ được biểu diễn qua hàm số \(f(x) = - 200{x^2} + 550x\). Công ty phải bán giá tour cho một khách là bao nhiêu (đơn vị: triệu đồng) để doanh thu từ tua xuyên Việt là lớn nhất (kết quả làm tròn đến hàng phần trăm)?
Đáp án:
Đáp án:
Tìm giá trị lớn nhất của hàm số f(x).
Ta có \(f'(x) = - 400x + 550 = 0 \Leftrightarrow x = \frac{{11}}{8}\).
Bảng biến thiên:
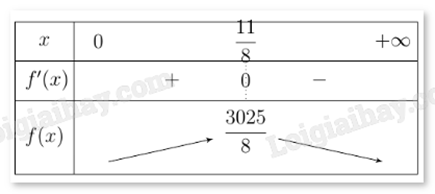
Ta thấy f(x) đạt giá trị lớn nhất khi \(x = \frac{{11}}{8} \approx 1,375\).
Vậy công ty cần bán tour với giá 1,38 triệu đồng/khách để doanh thu cao nhất.
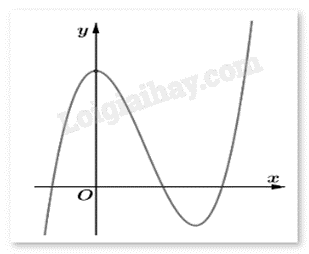
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \((a,b,c,d \in \mathbb{R})\) có đồ thị như hình:

Có bao nhiêu số dương trong các số a, b, c, d?
Đáp án:
Đáp án:
Dựa vào sự biến thiên, dấu của cực trị hàm số để xét dấu a, b, c, d.
Ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) nên a < 0.
Đồ thị cắt trục Oy tại điểm có tung độ dương nên d > 0.
Ta có: \(y' = 3a{x^2} + 2bx + c\). Hàm số đạt cực trị tại hai điểm \({x_1},{x_2} < 0\) nên:
\(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = \frac{{ - 2b}}{{3a}} \Rightarrow \frac{b}{a} > 0 \Rightarrow b < 0}\\{{x_1}.{x_2} = \frac{c}{{3a}} > 0 \Rightarrow c < 0}\end{array}} \right.\) (do a < 0)
Vậy có 1 số dương d.