Đề thi giữa kì 1 Toán 12 - Đề số 7
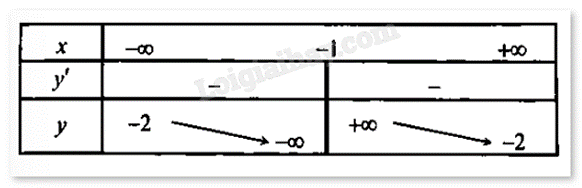
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
Đề bài
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
-
A.
Hàm số đã cho đồng biến trên khoảng \(( - \infty ; - 2)\) và \(( - 3;0)\)
-
B.
Hàm số đã cho nghịch biến trên khoảng \(( - 3; - 2)\)
-
C.
Hàm số đã cho đồng biến trên khoảng \((0;1)\)
-
D.
Hàm số đã cho nghịch biến trên khoảng \((0; + \infty )\)
Cho hàm số f(x) có đạo hàm \(f'(x) = x{(x + 1)^2}{(x - 2)^3}\), \(\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
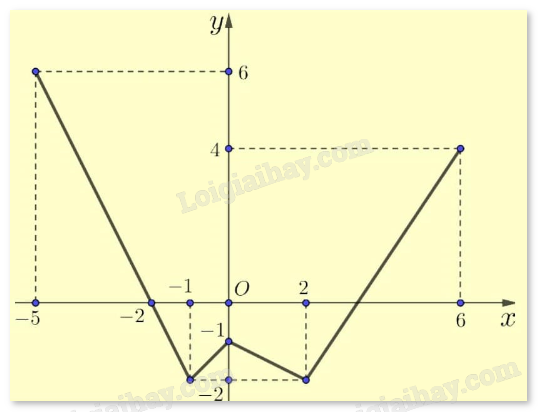
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2;2]. Tính M + m.
-
A.
-1
-
B.
-2
-
C.
0
-
D.
-3
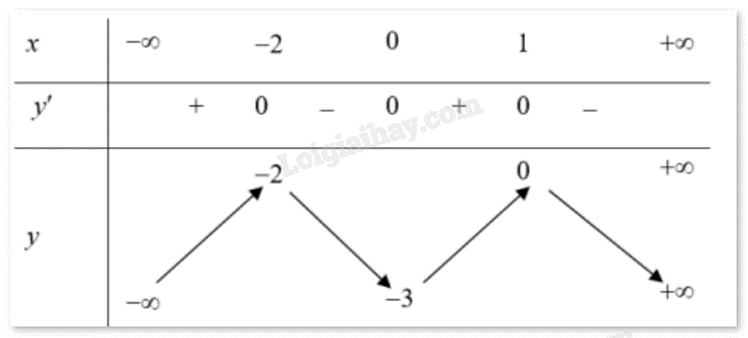
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?

-
A.
1
-
B.
4
-
C.
2
-
D.
3
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 3x}}{{x - 2}}\) là:
-
A.
\(y = x - 5\)
-
B.
\(y = 5x\)
-
C.
\(y = x + 5\)
-
D.
\(y = - x - 5\)
Tọa độ tâm đối xứng của đồ thị hàm số \(y = {x^3} - 3x + 1\) là:
-
A.
(-1;3)
-
B.
(1;0)
-
C.
(1;-1)
-
D.
(0;1)
Cho ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng. Trong các mệnh đề sau, mệnh đề nào sai?
-
A.
Nếu \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng thì từ \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) ta suy ra m = n = p = 0
-
B.
Nếu có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \), trong đó \({m^2} + {n^2} + {p^2} > 0\) thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
-
C.
Với ba số thực m, n, p thỏa mãn \(m + n + p \ne 0\) ta có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
-
D.
Nếu giá của \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng quy thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
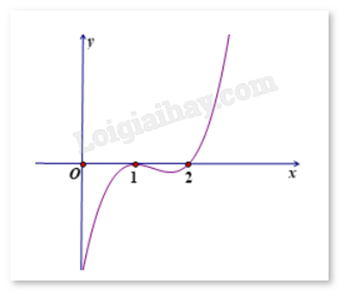
Hình bên là đồ thị của hàm số f’(x). Hỏi hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
-
A.
\((2; + \infty )\)
-
B.
\((1;2)\)
-
C.
\((0;1)\)
-
D.
\((0;1)\) và \((2; + \infty )\)
Đường cong hình bên là đồ thị của hàm số \(y = a{x^3} + b{x^2} + cx + d\) . Khẳng định nào sau đây đúng?
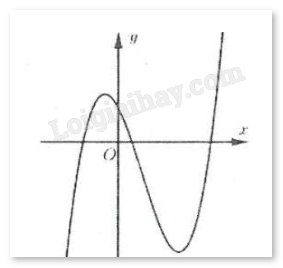
-
A.
a > 0, b < 0, c > 0, d > 0
-
B.
a > 0, b < 0, c < 0, d > 0
-
C.
a > 0, b > 0, c < 0, d > 0
-
D.
a < 0, b > 0, c > 0, d < 0
-
A.
\(y = \frac{{x - 4}}{{2x + 2}}\)
-
B.
\(y = \frac{{ - 2x - 4}}{{x + 1}}\)
-
C.
\(y = \frac{{ - 2x + 3}}{{x + 1}}\)
-
D.
\(y = \frac{{2 - x}}{{x + 1}}\)
Cho tứ diện hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN,SC) bằng
-
A.
\({45^o}\)
-
B.
\({30^o}\)
-
C.
\({90^o}\)
-
D.
\({60^o}\)
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \ne 0\). Xác định góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\).
-
A.
\(\alpha = {180^o}\)
-
B.
\(\alpha = {0^o}\)
-
C.
\(\alpha = {90^o}\)
-
D.
\(\alpha = {45^o}\)
a) Đồ thị hàm số đã cho có một 1 cực trị
b) Hàm số đã cho đồng biến trên R
c) Điểm (1;2) là tâm đối xứng của đồ thị hàm số y = f(x)
d) Đồ thị hàm số f(x) là \(y = {x^3} - 3{x^2} + 3x - 1\)
a) Đồ thị hàm số f(x) có tiệm cận đứng x = 0
b) Đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
c) Hàm số f(x) nghịch biến trên mỗi khoảng và
d) Đồ thị hàm số f(x) có điểm cực đại (-3;-4) và điểm cực tiểu (1;4)
a) \(\overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} = - \frac{{{a^2}}}{2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} \)
d) \(AB \bot CD\)
Trong không gian Oxyz, cho vecto \(\overrightarrow a = (2;3;1)\), \(\overrightarrow b = ( - 1;5;2)\), \(\overrightarrow c = (4; - 1;3)\) và \(\overrightarrow x = ( - 3;22;5)\).
a) \(\left| {2\overrightarrow a } \right| = 14\)
b) \(\left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {74} \)
c) \(3\overrightarrow a - 2\overrightarrow c = ( - 2;11; - 3)\)
d) \(\overrightarrow x = - 2\overrightarrow a - 3\overrightarrow b + \overrightarrow c \)
Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = \sqrt {1 - x} + \sqrt {1 + x} \) lần lượt là M, m. Tính \(M + 2{m^2}\).
Đáp án:
Với giá trị nào của tham số m để đồ thị hàm số \(y = \frac{{m{x^2} - 4}}{{mx - 1}}\) có tiệm cận đứng đi qua điểm A(1;4)?
Đáp án:
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Tính tổng của hoành độ, tung độ, cao độ đỉnh A’.
Đáp án:
Một chất điểm chuyển động theo quy luật \(s(t) = 6{t^2} - {t^3}\). Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động tại giá trị lớn nhất.
Đáp án:
Một khách sạn có 60 phòng. Chủ khách sạn nhận thấy nếu cho thuê mỗi phòng với giá 500 000 đồng/ngày thì tất cả các phòng đều được thuê hết và cứ tăng giá thêm 50 000 đồng một phòng thì có thêm 2 phòng trống. Hỏi chủ khách sạn nên cho thuê mỗi phòng với giá bao nhiêu tiền (đơn vị: nghìn đồng) một ngày để tổng doanh thu một ngày là lớn nhất.
Đáp án:
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình. Biết a là số thực dương, hỏi trong các số a, c, d có tất cả bao nhiêu số dương?
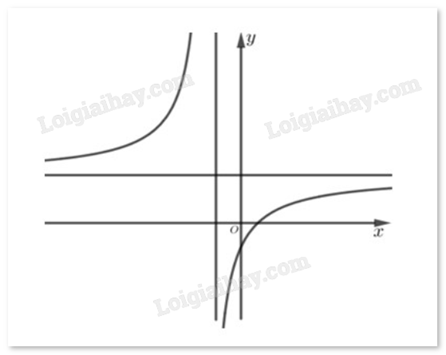
Đáp án:
Lời giải và đáp án
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?

-
A.
Hàm số đã cho đồng biến trên khoảng \(( - \infty ; - 2)\) và \(( - 3;0)\)
-
B.
Hàm số đã cho nghịch biến trên khoảng \(( - 3; - 2)\)
-
C.
Hàm số đã cho đồng biến trên khoảng \((0;1)\)
-
D.
Hàm số đã cho nghịch biến trên khoảng \((0; + \infty )\)
Đáp án : B
Quan sát bảng biến thiên và nhận xét.
Nhìn vào bảng biến thiên ta thấy đồ thị hàm số đã cho đồng biến trên khoảng (-∞;-2) và (0;1); nghịch biến trên khoảng (-2;0) và (1;+∞).
Cho hàm số f(x) có đạo hàm \(f'(x) = x{(x + 1)^2}{(x - 2)^3}\), \(\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Đáp án : B
\({x_0}\) là điểm cực trị của hàm số \(f(x)\) nếu \(f'({x_0}) = 0\) và \(f'({x_0})\) đổi dấu qua \({x_0}\).
\(f'(x) = x{(x + 1)^2}{(x - 2)^3} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = - 1}\\{x = 2}\end{array}} \right.\).
\(f'(x)\) đổi dấu qua \(x = 0\), \(x = 2\).
Vậy số điểm cực trị của hàm số là 2.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2;2]. Tính M + m.
-
A.
-1
-
B.
-2
-
C.
0
-
D.
-3
Đáp án : B
Quan sát đồ thị và nhận xét.
Dựa vào đồ thị ta thấy:
\(\mathop {\max }\limits_{[ - 2;2]} f(x) = f(2) = 0\), \(\mathop {\min }\limits_{[ - 2;2]} f(x) = f( - 1) = f(2) = - 2\). Vậy M + m = 0 + (-2) = -2.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?

-
A.
1
-
B.
4
-
C.
2
-
D.
3
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Dựa vào bảng biến thiên ta có: \(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = + \infty \) nên x = 1 là tiệm cận đứng của đồ thị hàm số.
Mặt khác: \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 1\), \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - 1\) nên y = 1, y = -1 là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị có 3 tiệm cận.
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 3x}}{{x - 2}}\) là:
-
A.
\(y = x - 5\)
-
B.
\(y = 5x\)
-
C.
\(y = x + 5\)
-
D.
\(y = - x - 5\)
Đáp án : C
Thực hiện phép chia đa thức (ở tử) cho đa thức (ở mẫu) ta được \(y = ax + b + \frac{M}{{cx + d}}\)(a≠0) với M là hằng số.
Đường thẳng y = ax + b (a≠0) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
Kết luận đường thẳng y = ax +b là đường tiệm cận xiên của đồ thị hàm số.
Ta có: \(y = y = \frac{{{x^2} + 3x}}{{x - 2}} = x + 5 + \frac{{10}}{{x - 2}} = f(x)\).
Từ đó: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - \left( {x + 5} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{10}}{{x - 2}} = 0\).
Vậy đường thẳng \(y = x + 5\) là đường tiệm cận xiên của đồ thị hàm số đã cho.
Tọa độ tâm đối xứng của đồ thị hàm số \(y = {x^3} - 3x + 1\) là:
-
A.
(-1;3)
-
B.
(1;0)
-
C.
(1;-1)
-
D.
(0;1)
Đáp án : D
Tìm điểm thuộc đồ thị có hoành độ tại y’’=0.
\(y' = 3{x^2} - 3\), \(y'' = 6x = 0 \Leftrightarrow x = 0\).
Thay x = 0 vào hàm số, được y = 1.
Cho ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng. Trong các mệnh đề sau, mệnh đề nào sai?
-
A.
Nếu \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng thì từ \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) ta suy ra m = n = p = 0
-
B.
Nếu có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \), trong đó \({m^2} + {n^2} + {p^2} > 0\) thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
-
C.
Với ba số thực m, n, p thỏa mãn \(m + n + p \ne 0\) ta có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
-
D.
Nếu giá của \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng quy thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
Đáp án : D
Dựa vào lý thuyết vecto cùng phương, vecto đồng phẳng.
Câu D sai. Ví dụ phản chứng: 3 cạnh của hình chóp tam giác đồng quy tại 1 đỉnh nhưng chúng không đồng phẳng.
Hình bên là đồ thị của hàm số f’(x). Hỏi hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

-
A.
\((2; + \infty )\)
-
B.
\((1;2)\)
-
C.
\((0;1)\)
-
D.
\((0;1)\) và \((2; + \infty )\)
Đáp án : A
Quan sát đồ thị và nhận xét.
Dựa vào đồ thị ta thấy \(f'(x) > 0,\forall x > 2\) nên y = f(x) đồng biến trên \((2; + \infty )\) .
Đường cong hình bên là đồ thị của hàm số \(y = a{x^3} + b{x^2} + cx + d\) . Khẳng định nào sau đây đúng?

-
A.
a > 0, b < 0, c > 0, d > 0
-
B.
a > 0, b < 0, c < 0, d > 0
-
C.
a > 0, b > 0, c < 0, d > 0
-
D.
a < 0, b > 0, c > 0, d < 0
Đáp án : B
Dựa vào sự biến thiên và cực trị của hàm số để xét dấu.
Dựa vào đồ thị ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) nên a > 0. Loại D.
Đồ thị đi qua điểm (0;d) nên d > 0 (vì đồ thị cắt trục tung tại điểm có tung độ dương).
Hàm số đạt cực trị tại hai điểm \({x_1},{x_2}\). Dựa vào hình vẽ ta thấy \({x_1} < 0,x{}_2 > 0\) và \({x_1} + {x_2} > 0\).
Mặt khác, \(y' = 3a{x^2} + 2bx + c \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = \frac{{ - 2b}}{{3a}} > 0 \Rightarrow b < 0}\\{{x_1}{x_2} = \frac{c}{{3a}} < 0 \Rightarrow c < 0}\end{array}} \right.\)
-
A.
\(y = \frac{{x - 4}}{{2x + 2}}\)
-
B.
\(y = \frac{{ - 2x - 4}}{{x + 1}}\)
-
C.
\(y = \frac{{ - 2x + 3}}{{x + 1}}\)
-
D.
\(y = \frac{{2 - x}}{{x + 1}}\)
Đáp án : C
Dựa vào sự biến thiên, tiệm cận và các điểm hàm số đi qua để lập hệ phương trình tìm hệ số.
Đồ thị hàm số có tiệm cận đứng x = -1 và tiệm cận ngang y = -2. Loại A và D.
Xét hàm số \(y = \frac{{ - 2x - 4}}{{x + 1}}\) có \(y' = \frac{2}{{{{(x + 1)}^2}}} > 0\). Hàm số đồng biến trên các khoảng xác định của nó.
Xét hàm số \(y = \frac{{ - 2x + 3}}{{x + 1}}\) có \(y' = \frac{{ - 5}}{{{{(x + 1)}^2}}} < 0\). Hàm số nghịch biến trên các khoảng xác định của nó.
Mà theo bảng biến thiên thì hàm số nghịch biến. Ta chọn hàm số \(y = \frac{{ - 2x + 3}}{{x + 1}}\).
Cho tứ diện hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN,SC) bằng
-
A.
\({45^o}\)
-
B.
\({30^o}\)
-
C.
\({90^o}\)
-
D.
\({60^o}\)
Đáp án : C
Tính góc thông qua tích vô hướng của 2 vecto.
Ta có: \(AC = a\sqrt 2 \Rightarrow A{C^2} = 2{a^2} = {a^2} + {a^2} = S{A^2} + S{C^2}\). Suy ra \(\Delta SAC\) vuông tại S.
Khi đó: \(\overrightarrow {NM} .\overrightarrow {SC} = \frac{1}{2}\overrightarrow {SA} .\overrightarrow {SC} = 0\). Suy ra \(\left( {\overrightarrow {NM} ,\overrightarrow {SC} } \right) = {90^o}\), tức \(\left( {MN,SC} \right) = {90^o}\).
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \ne 0\). Xác định góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\).
-
A.
\(\alpha = {180^o}\)
-
B.
\(\alpha = {0^o}\)
-
C.
\(\alpha = {90^o}\)
-
D.
\(\alpha = {45^o}\)
Đáp án : A
Sử dụng công thức tính tích góc giữa hai vecto.
Ta có: \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| \Rightarrow \cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = - 1 \Rightarrow (\overrightarrow a ,\overrightarrow b ) = {180^o}\).
a) Đồ thị hàm số đã cho có một 1 cực trị
b) Hàm số đã cho đồng biến trên R
c) Điểm (1;2) là tâm đối xứng của đồ thị hàm số y = f(x)
d) Đồ thị hàm số f(x) là \(y = {x^3} - 3{x^2} + 3x - 1\)
a) Đồ thị hàm số đã cho có một 1 cực trị
b) Hàm số đã cho đồng biến trên R
c) Điểm (1;2) là tâm đối xứng của đồ thị hàm số y = f(x)
d) Đồ thị hàm số f(x) là \(y = {x^3} - 3{x^2} + 3x - 1\)
Quan sát đồ thị và nhận xét.
a) Sai . Hàm số f(x) không có cực trị.
b) Đúng . Hàm số đã cho đồng biến trên R.
c) Đúng. Điểm (1;2) là tâm đối xứng của đồ thị hàm số y = f(x) vì nó là điểm uốn của đồ thị.
d) Sai. Đồ thị hàm số \(y = {x^3} - 3{x^2} + 3x - 1\) cắt trục tung tại điểm (0;-1), còn đồ thị trên hình vẽ cắt trục tung tại điểm (0;1).
a) Đồ thị hàm số f(x) có tiệm cận đứng x = 0
b) Đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
c) Hàm số f(x) nghịch biến trên mỗi khoảng và
d) Đồ thị hàm số f(x) có điểm cực đại (-3;-4) và điểm cực tiểu (1;4)
a) Đồ thị hàm số f(x) có tiệm cận đứng x = 0
b) Đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
c) Hàm số f(x) nghịch biến trên mỗi khoảng và
d) Đồ thị hàm số f(x) có điểm cực đại (-3;-4) và điểm cực tiểu (1;4)
Quan sát đồ thị và nhận xét.
a) Sai. Đồ thị hàm số f(x) có tiệm cận đứng x = -1.
b) Sai. Tâm đối xứng của đồ thị là điểm (-1;0).
c) Sai. Hàm số f(x) đồng biến trên mỗi khoảng \(( - \infty ; - 3)\) và \((1; + \infty )\)
d) Đúng. Đồ thị hàm số f(x) có điểm cực đại (-3;-4) và điểm cực tiểu (1;4) .
a) \(\overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} = - \frac{{{a^2}}}{2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} \)
d) \(AB \bot CD\)
a) \(\overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} = - \frac{{{a^2}}}{2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} \)
d) \(AB \bot CD\)
Sử dụng quy tắc cộng vecto, lý thuyết các vecto bằng nhau, vecto đối nhau, công thức tính góc giữa hai vecto.
a) Đúng . \(\overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow {AD} + \overrightarrow {DA} + \overrightarrow {BC} + \overrightarrow {CB} = \overrightarrow 0 \) .
b) Đúng. \(\overrightarrow {AB} .\overrightarrow {BC} = - \overrightarrow {BA} .\overrightarrow {BC} = - a.a.\cos {60^o} = - \frac{{{a^2}}}{2}\) .
c) Sai . \(\overrightarrow {AC} .\overrightarrow {AD} = a.a.\cos {60^o} = \frac{{{a^2}}}{2}\) , \(\overrightarrow {AC} .\overrightarrow {CD} = - \overrightarrow {CA} .\overrightarrow {CD} = - a.a.\cos {60^o} = - \frac{{{a^2}}}{2}\) .
d) Đúng. Giả sử I là trung điểm của CD thì \(CD \bot (ABI)\), suy ra \(CD \bot AB\).
Trong không gian Oxyz, cho vecto \(\overrightarrow a = (2;3;1)\), \(\overrightarrow b = ( - 1;5;2)\), \(\overrightarrow c = (4; - 1;3)\) và \(\overrightarrow x = ( - 3;22;5)\).
a) \(\left| {2\overrightarrow a } \right| = 14\)
b) \(\left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {74} \)
c) \(3\overrightarrow a - 2\overrightarrow c = ( - 2;11; - 3)\)
d) \(\overrightarrow x = - 2\overrightarrow a - 3\overrightarrow b + \overrightarrow c \)
a) \(\left| {2\overrightarrow a } \right| = 14\)
b) \(\left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {74} \)
c) \(3\overrightarrow a - 2\overrightarrow c = ( - 2;11; - 3)\)
d) \(\overrightarrow x = - 2\overrightarrow a - 3\overrightarrow b + \overrightarrow c \)
Sử dụng các quy tắc cộng vecto, công thức tính tích vô hướng của hai vecto, độ dài vecto.
a) Sai . Vì \(\left| {2\overrightarrow a } \right| = \sqrt {{4^2} + {6^2} + {2^2}} = 2\sqrt {14} \).
b) Đúng. Vì \(\left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {{1^2} + {8^2} + {3^2}} = \sqrt {74} \).
c) Đúng . Vì \(3\overrightarrow a - 2\overrightarrow c = (6;9;3) - (8; - 2;6) = ( - 2;11; - 3)\)
d) Sai. Đặt \(\overrightarrow x = m\overrightarrow a + n\overrightarrow b + p\overrightarrow c \) với \(m,n,p \in R\).
Suy ra \(( - 3;22;5) = m(2;3;1) + n( - 1;5;2) + p(;4; - 1;3) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2m - n + 4p = - 3}\\{3m + 5n - p = 22}\\{m + 2n + 3p = 5}\end{array}} \right.\)
Giải hệ trên ta được m = 2, n = 3, p = -1. Vậy \(\overrightarrow x = 2\overrightarrow a + 3\overrightarrow b - \overrightarrow c \).
Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = \sqrt {1 - x} + \sqrt {1 + x} \) lần lượt là M, m. Tính \(M + 2{m^2}\).
Đáp án:
Đáp án:
- Tính y’, tìm các nghiệm của y’ = 0.
- Tìm giá trị y tại các điểm cực trị của hàm số và hai đầu mút của đoạn.
Tập xác định: D = [-1;1].
Ta có: \(f'(x) = - \frac{1}{{2\sqrt {1 - x} }} + \frac{1}{{2\sqrt {1 + x} }} = - \frac{{\sqrt {1 + x} }}{{2\sqrt {1 - x} }} + \frac{{\sqrt {1 - x} }}{{2\sqrt {1 + x} }} = 0\)
\( \Leftrightarrow \sqrt {1 - x} = \sqrt {1 + x} \Leftrightarrow x = 0\).
\(f( - 1) = f(1) = \sqrt 2 \); f(0) = 2.
Vậy \(M + 2{m^2} = 2 + 2.{\left( {\sqrt 2 } \right)^2} = 6\).
Với giá trị nào của tham số m để đồ thị hàm số \(y = \frac{{m{x^2} - 4}}{{mx - 1}}\) có tiệm cận đứng đi qua điểm A(1;4)?
Đáp án:
Đáp án:
Sử dụng quy tắc tìm đường tiệm cận của hàm phân thức.
Tiệm cận đứng của đồ thị hàm số là \(x = \frac{1}{m}\).
Tiệm cận đứng của đồ thị hàm số đi qua điểm A(1;4) nên \(\frac{1}{m} = 1 \Leftrightarrow m = 1\).
Thử lại thấy thỏa mãn.
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Tính tổng của hoành độ, tung độ, cao độ đỉnh A’.
Đáp án:
Đáp án:
Sử dụng quy tắc hình hộp.
Theo quy tắc hình hộp, ta có: \(\overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC'} \), suy ra \(\overrightarrow {AA'} = \overrightarrow {AC'} - \overrightarrow {AB} - \overrightarrow {AD} \).
Lại có: \(\overrightarrow {AC'} = (3;5; - 6)\), \(\overrightarrow {AB} = (1;1;1)\), \(\overrightarrow {AD} = (0; - 1;0)\).
Do đó:
\(\overrightarrow {AA'} = (2;5; - 7)\), suy ra \(A'(3;5; - 6)\). Tổng cần tìm là 3 + 5 + (-6) = 2.
Một chất điểm chuyển động theo quy luật \(s(t) = 6{t^2} - {t^3}\). Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động tại giá trị lớn nhất.
Đáp án:
Đáp án:
Lập bảng biến thiên và tìm giá trị lớn nhất của hàm số.
Theo giả thiết: \(s(t) = 6{t^2} - {t^3}\), \(t \in (0; + \infty )\).
Vận tốc của chuyển động là \(v(t) = s'(t) = 12t - 3{t^2}\).
Ta có: \(v'(t) = 12 - 6t = 0 \Leftrightarrow t = 2\).
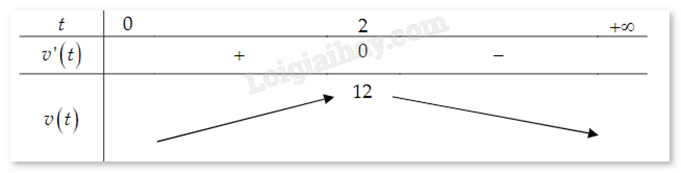
Dựa vào bảng biến thiên, ta thấy vận tốc đạt giá trị lớn nhất khi t = 2.
Một khách sạn có 60 phòng. Chủ khách sạn nhận thấy nếu cho thuê mỗi phòng với giá 500 000 đồng/ngày thì tất cả các phòng đều được thuê hết và cứ tăng giá thêm 50 000 đồng một phòng thì có thêm 2 phòng trống. Hỏi chủ khách sạn nên cho thuê mỗi phòng với giá bao nhiêu tiền (đơn vị: nghìn đồng) một ngày để tổng doanh thu một ngày là lớn nhất.
Đáp án:
Đáp án:
Lập hàm số tính doanh thu một ngày của khách sạn và tìm giá trị lớn nhất.
Gọi giá tiền chủ khách sạn cho thuê một phòng là x (\(x \ge 500\)).
Vì cứ tăng giá thêm 50 000 đồng một phòng thì có thêm 2 phòng trống nên số phòng được thuê là:
\(60 - \frac{{x - 500}}{{50}}.2 = 80 - \frac{x}{{25}}\).
Khi đó, tổng doanh thu 1 ngày là \(x\left( {80 - \frac{x}{{25}}} \right) = 80x - \frac{{{x^2}}}{{25}} = f(x)\).
Ta có \(f'(x) = 80 - \frac{{2x}}{{25}} = 0 \Leftrightarrow x = 1000\).
Vì \(f(x)\) là tam thức bậc hai có hệ số cao nhất âm nên f(x) đạt giá trị lớn nhất tại x = 1000.
Vậy để tổng doanh thu lớn nhất thì thì chủ khách sạn nên cho thuê phòng với giá 1000 nghìn đồng/ngày (tức 1 triệu đồng).
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình. Biết a là số thực dương, hỏi trong các số a, c, d có tất cả bao nhiêu số dương?

Đáp án:
Đáp án:
Quan sát đồ thị.
Đường tiệm cận ngang của đồ thị là \(y = \frac{a}{c}\) cắt trục tung tại điểm có tung độ dương nên a.c > 0. Vì a > 0 nên c > 0.
Đường tiệm cận đứng của đồ thị là \(x = \frac{{ - d}}{c}\) cắt trục hoành tại điểm có hoành độ âm nên -d.c < 0 hay c.d > 0. Vì c > 0 nên d > 0.
Đồ thị cắt trục tung tại điểm có tung độ âm nên \(\frac{b}{d} < 0\). Mà d > 0 nên b < 0.
Vậy ta có a, c, d là các số dương.