Đề thi giữa kì 1 Toán 12 - Đề số 6
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây sai?
Đề bài
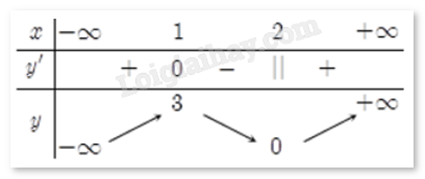
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây sai?
-
A.
Hàm số đã cho đồng biến trên khoảng \((2; + \infty )\)
-
B.
Hàm số đã cho đồng biến trên khoảng \((3; + \infty )\)
-
C.
Hàm số đã cho đồng biến trên khoảng \(( - \infty ;1)\)
-
D.
Hàm số đã cho nghịch biến trên khoảng (0;3)
-
A.
\(y = \frac{{2x + 1}}{{x - 1}}\)
-
B.
\(y = {x^3} - 3x\)
-
C.
\(y = - {x^4} + 2{x^2} - 1\)
-
D.
\(y = - {x^3} - 3x\)
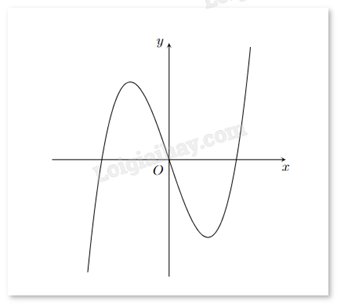
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
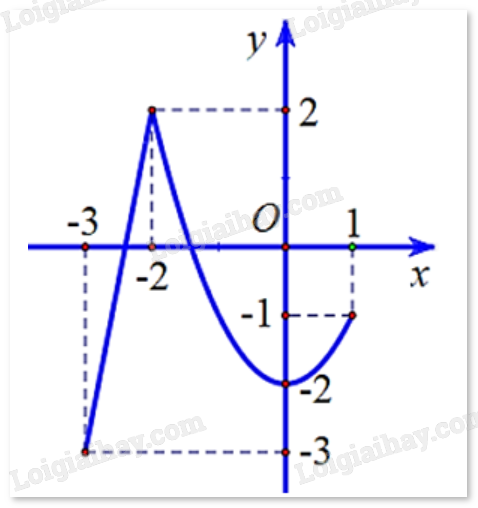
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-3;1]. Tính M + m.
-
A.
-1
-
B.
-2
-
C.
0
-
D.
-3
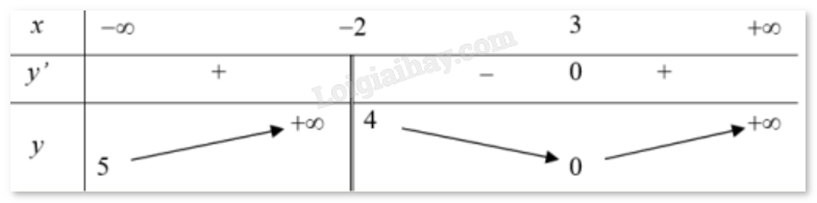
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
-
A.
2
-
B.
3
-
C.
4
-
D.
1
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 4x + 2}}{{ - 2x + 3}}\) là:
-
A.
\(y = - \frac{1}{2}x - \frac{5}{4}\)
-
B.
\(y = \frac{1}{2}x + \frac{5}{4}\)
-
C.
\(y = \frac{1}{2}x - \frac{5}{4}\)
-
D.
\(y = - \frac{1}{2}x + \frac{5}{4}\)
Tọa độ tâm đối xứng của đồ thị hàm số \(y = {x^3} + 3{x^2} - 9x + 1\) là:
-
A.
(-1;6)
-
B.
(-1;12)
-
C.
(1;4)
-
D.
(-3;28)
Trong không gian, gọi \(\alpha \) là góc giữa hai vecto \(\overrightarrow m \) và \(\overrightarrow n \) khác vecto không. Khẳng định nào sau đây đúng?
-
A.
\({0^o} \le \alpha \le {180^o}\)
-
B.
\({0^o} < \alpha < {180^o}\)
-
C.
\({0^o} \le \alpha \le {90^o}\)
-
D.
\({0^o} < \alpha < {90^o}\)
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm (\(0 \le x \le 300\)) được cho bởi hàm số \(y = - {x^3} + 300{x^2}\) (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới.
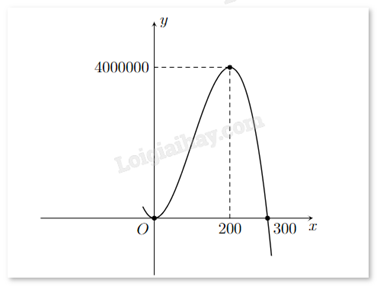
Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận dự kiến thu được nhiều nhất?
-
A.
4000000
-
B.
200
-
C.
300
-
D.
150
Giá trị lớn nhất của hàm số \(y = \frac{{{x^2} + 2x + 3}}{{x - 1}}\) là:
-
A.
8
-
B.
9
-
C.
1
-
D.
3
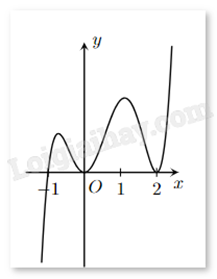
Hàm số f(x) có đạo hàm f’(x) trên khoảng K. Hình vẽ dưới là đồ thị của hàm số f’(x) trên khoảng K. Hỏi hàm số f(x) có bao nhiêu điểm cực trị?
-
A.
1
-
B.
2
-
C.
0
-
D.
3
Cho tứ diện ABCD có AB = AC = AD và \(\widehat {BAC} = \widehat {BAD} = {60^o}\). Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \).
-
A.
\({60^o}\)
-
B.
\({45^o}\)
-
C.
\({120^o}\)
-
D.
\({90^o}\)
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1\) và \(\overrightarrow a .\overrightarrow b = 3\). Độ dài vecto \(3\overrightarrow a + 5\overrightarrow b \) là?
-
A.
\(5\sqrt 5 \)
-
B.
\(\sqrt {124} \)
-
C.
8
-
D.
124
a) Hàm số f(x) đồng biến trên (-1;1)
b) Số điểm cực trị của hàm số đã cho là 2
c) Hàm số f(x) không có giá trị lớn nhất và nhỏ nhất
d) Đồ thị hàm số f(x) là \(y = {x^3} - 3x\)
a) Đồ thị hàm số f(x) có tiệm cận đứng và tiệm cận xiên
b) Đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
c) Hàm số f(x) có giá trị lớn nhất là -4
d) Đồ thị hàm số f(x) có điểm cực đại (2;4) và điểm cực tiểu (-2;-4)
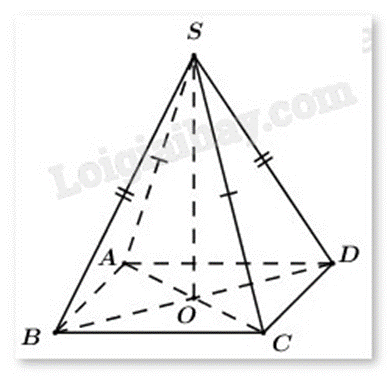
a) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \)
b) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} = \overrightarrow {CD} \)
c) Nếu có \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thì tứ giác ABCD là hình bình hành
d) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
Trong không gian Oxyz, cho vecto \(\overrightarrow c = (3;4;0)\), \(\overrightarrow b = (1; - 2;2)\).
a) \(\left| {\overrightarrow a } \right| = 5\)
b) \(\overrightarrow c + \overrightarrow d = (4;2;2)\)
c) \(\overrightarrow c .\overrightarrow d = 1\)
d) Góc giữa hai vecto \(\overrightarrow c ,\overrightarrow d \) bằng \({90^o}\)
Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = x\sqrt {1 - {x^2}} \) lần lượt là M, m. Tính M + m.
Đáp án:
Tính tổng tất cả các giá trị thực của tham số m để đồ thị hàm số \(y = \frac{{{x^2} + m}}{{{x^2} - 3x + 2}}\) có đúng 2 đường tiệm cận.
Đáp án:
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết A(2;4;0), B(4;0;0), C(-1;4;-7) và D’(6;8;10). Tổng hoành độ, tung độ, cao độ của điểm B’ bằng bao nhiêu?
Đáp án:
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G(x) = 0,035{x^2}(15 - x)\), trong đó x là liều lượng thuốc được tiêm cho bệnh nhân (x được tính bằng milligram). Tính liều lượng thuốc cần tiêm (đơn vị milligram) cho bệnh nhân để huyết áp giảm nhiều nhất.
Đáp án:
Giá trị của tham số m để đồ thị hàm số \(y = {x^3} - 3{x^2} + m\) có hai điểm cực trị A, B thỏa mãn OA = OB (O là gốc tọa độ) có dạng \(\frac{a}{b}\) là một phân số tối giản. Tính a + b.
Đáp án:
Cho hàm số y = f(x) có đồ thị như hình:
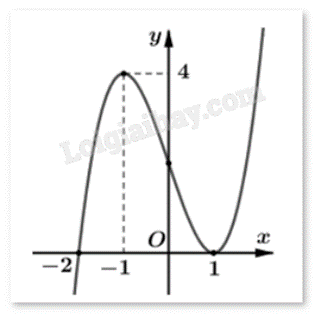
Tìm số điểm cực trị của hàm số \(g(x) = f({x^2} - 3)\).
Đáp án:
Lời giải và đáp án
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây sai?

-
A.
Hàm số đã cho đồng biến trên khoảng \((2; + \infty )\)
-
B.
Hàm số đã cho đồng biến trên khoảng \((3; + \infty )\)
-
C.
Hàm số đã cho đồng biến trên khoảng \(( - \infty ;1)\)
-
D.
Hàm số đã cho nghịch biến trên khoảng (0;3)
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Nhìn vào bảng biến thiên ta thấy đồ thị hàm số đã cho đồng biến trên khoảng (-∞;1) và (2;+∞); nghịch biến trên khoảng (1;2).
-
A.
\(y = \frac{{2x + 1}}{{x - 1}}\)
-
B.
\(y = {x^3} - 3x\)
-
C.
\(y = - {x^4} + 2{x^2} - 1\)
-
D.
\(y = - {x^3} - 3x\)
Đáp án : B
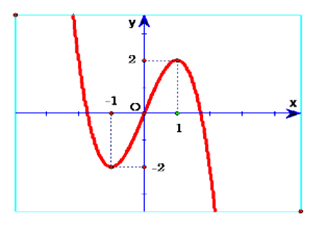
Quan sát đồ thị và nhận xét.
Ta có đây là đồ thị hàm số bậc 3 dạng \(y = a{x^3} + b{x^2} + cx + d\), mặt khác hệ số a > 0 (vì \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)).
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-3;1]. Tính M + m.
-
A.
-1
-
B.
-2
-
C.
0
-
D.
-3
Đáp án : A
Quan sát đồ thị và nhận xét.
Dựa vào đồ thị ta thấy:
\(\mathop {\max }\limits_{[ - 3;1]} f(x) = 2\), \(\mathop {\min }\limits_{[ - 3;1]} g(x) = - 3\). Vậy M + m = 2 + (-3) = -1.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?

-
A.
2
-
B.
3
-
C.
4
-
D.
1
Đáp án : A
Quan sát bảng biến thiên và nhận xét.
Dựa vào bảng biến thiên ta có: \(\mathop {\lim }\limits_{x \to {{( - 2)}^ - }} f(x) = + \infty \) nên x = -2 là tiệm cận đứng của đồ thị hàm số.
Mặt khác: \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 5\) nên y = 5 là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị có 2 tiệm cận.
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 4x + 2}}{{ - 2x + 3}}\) là:
-
A.
\(y = - \frac{1}{2}x - \frac{5}{4}\)
-
B.
\(y = \frac{1}{2}x + \frac{5}{4}\)
-
C.
\(y = \frac{1}{2}x - \frac{5}{4}\)
-
D.
\(y = - \frac{1}{2}x + \frac{5}{4}\)
Đáp án : D
Thực hiện phép chia đa thức (ở tử) cho đa thức (ở mẫu) ta được \(y = ax + b + \frac{M}{{cx + d}}\)(a≠0) với M là hằng số.
Đường thẳng y = ax + b (a≠0) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
Kết luận đường thẳng y = ax +b là đường tiệm cận xiên của đồ thị hàm số.
Ta có: \(y = \frac{{{x^2} - 4x + 2}}{{ - 2x + 3}} = - \frac{1}{2}x + \frac{5}{4} - \frac{{15}}{{4( - 2x + 3)}} = f(x)\).
Từ đó: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - \left( { - \frac{1}{2}x + \frac{5}{4}} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } - \frac{{15}}{{4( - 2x + 3)}} = 0\).
Vậy đường thẳng \(y = - \frac{1}{2}x + \frac{5}{4}\) là đường tiệm cận xiên của đồ thị hàm số đã cho.
Tọa độ tâm đối xứng của đồ thị hàm số \(y = {x^3} + 3{x^2} - 9x + 1\) là:
-
A.
(-1;6)
-
B.
(-1;12)
-
C.
(1;4)
-
D.
(-3;28)
Đáp án : B
Tìm điểm thuộc đồ thị có hoành độ tại y’’ = 0.
\(y' = 3{x^2} + 6x - 9\), \(y'' = 6x + 6 = 0 \Leftrightarrow x = - 1\).
Thay x = -1 vào hàm số, được y = 12.
Trong không gian, gọi \(\alpha \) là góc giữa hai vecto \(\overrightarrow m \) và \(\overrightarrow n \) khác vecto không. Khẳng định nào sau đây đúng?
-
A.
\({0^o} \le \alpha \le {180^o}\)
-
B.
\({0^o} < \alpha < {180^o}\)
-
C.
\({0^o} \le \alpha \le {90^o}\)
-
D.
\({0^o} < \alpha < {90^o}\)
Đáp án : A
Lý thuyết góc giữa hai vecto trong không gian.
Góc giữa hai vecto có tập giá trị từ \({0^o}\) đến \({180^o}\).
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm (\(0 \le x \le 300\)) được cho bởi hàm số \(y = - {x^3} + 300{x^2}\) (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới.

Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận dự kiến thu được nhiều nhất?
-
A.
4000000
-
B.
200
-
C.
300
-
D.
150
Đáp án : B
Quan sát đồ thị và nhận xét.
Lợi nhuận đạt giá trị lớn nhất là 4000000 đồng khi sản xuất 200 sản phẩm.
Giá trị lớn nhất của hàm số \(y = \frac{{{x^2} + 2x + 3}}{{x - 1}}\) là:
-
A.
8
-
B.
9
-
C.
1
-
D.
3
Đáp án : B
Tìm đạo hàm của hàm số sau đó tính các giá trị f(x).
Hàm số xác định trên (1;3].
\(f'(x) = \frac{{{x^2} - 2x - 5}}{{{{(x + 1)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 + \sqrt 6 \notin (1;3]}\\{x = 1 - \sqrt 6 \notin (1;3]}\end{array}} \right.\)
Vì \(x \in \left[ {0;\frac{{3\pi }}{2}} \right]\) nên \(f'(x) = 0 \Leftrightarrow x = 0,x = \frac{\pi }{3}\).

Vậy giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} + 2x + 3}}{{x - 1}}\) bằng 9.
Hàm số f(x) có đạo hàm f’(x) trên khoảng K. Hình vẽ dưới là đồ thị của hàm số f’(x) trên khoảng K. Hỏi hàm số f(x) có bao nhiêu điểm cực trị?

-
A.
1
-
B.
2
-
C.
0
-
D.
3
Đáp án : A
Hàm số đạt cực trị tại \({x_0}\) khi f’(x) đổi dấu khi đi qua \({x_0}\).
Quan sát đồ thị thấy f’(x) đổi dấu khi đi qua x = -1. Vậy f(x) có duy nhất 1 điểm cực trị là x = -1.
Cho tứ diện ABCD có AB = AC = AD và \(\widehat {BAC} = \widehat {BAD} = {60^o}\). Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \).
-
A.
\({60^o}\)
-
B.
\({45^o}\)
-
C.
\({120^o}\)
-
D.
\({90^o}\)
Đáp án : D
Tính góc thông qua tích vô hướng của 2 vecto.
Ta có: \(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \)
\( = AB.AD.\cos {60^o} - AB.AC.\cos {60^o} = 0\).
Suy ra \(\left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = {90^o}\).
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1\) và \(\overrightarrow a .\overrightarrow b = 3\). Độ dài vecto \(3\overrightarrow a + 5\overrightarrow b \) là?
-
A.
\(5\sqrt 5 \)
-
B.
\(\sqrt {124} \)
-
C.
8
-
D.
124
Đáp án : B
Sử dụng công thức tính tích vô hướng của hai vecto và tính độ dài vecto.
\({\left( {3\overrightarrow a + 5\overrightarrow b } \right)^2} = 9{\overrightarrow a ^2} + 30\overrightarrow a \overrightarrow b + 25{\overrightarrow b ^2} = 9 + 90 + 25 = 124 \Rightarrow \left| {3\overrightarrow a + 5\overrightarrow b } \right| = \sqrt {124} \).
a) Hàm số f(x) đồng biến trên (-1;1)
b) Số điểm cực trị của hàm số đã cho là 2
c) Hàm số f(x) không có giá trị lớn nhất và nhỏ nhất
d) Đồ thị hàm số f(x) là \(y = {x^3} - 3x\)
a) Hàm số f(x) đồng biến trên (-1;1)
b) Số điểm cực trị của hàm số đã cho là 2
c) Hàm số f(x) không có giá trị lớn nhất và nhỏ nhất
d) Đồ thị hàm số f(x) là \(y = {x^3} - 3x\)
Quan sát đồ thị và nhận xét.
a) Đúng . Hàm số f(x) đồng biến trên (-1;1).
b) Đúng . Hàm số có 2 điểm cực trị là x = 1; x = -1.
c) Đúng. Hàm số đã cho không có giá trị lớn nhất và nhỏ nhất.
d) Sai. Đồ thị hàm số là \(y = - {x^3} + 3x\).
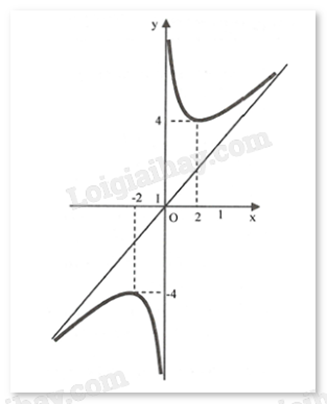
a) Đồ thị hàm số f(x) có tiệm cận đứng và tiệm cận xiên
b) Đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
c) Hàm số f(x) có giá trị lớn nhất là -4
d) Đồ thị hàm số f(x) có điểm cực đại (2;4) và điểm cực tiểu (-2;-4)
a) Đồ thị hàm số f(x) có tiệm cận đứng và tiệm cận xiên
b) Đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
c) Hàm số f(x) có giá trị lớn nhất là -4
d) Đồ thị hàm số f(x) có điểm cực đại (2;4) và điểm cực tiểu (-2;-4)
Quan sát đồ thị và nhận xét.
a) Đúng. Đồ thị hàm số f(x) có tiệm cận đứng x = 0 và tiệm cận xiên y = 2x.
b) Đúng. Vì gốc tọa độ O là trung điểm của 2 cực trị (2;4) và (-2;-4) nên là tâm đối xứng của đồ thị.
c) Sai. Hàm số không có giá trị lớn nhất.
d) Sai. Đồ thị hàm số f(x) có điểm cực tiểu (2;4) và điểm cực đại (-2;-4) .
a) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \)
b) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} = \overrightarrow {CD} \)
c) Nếu có \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thì tứ giác ABCD là hình bình hành
d) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
a) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \)
b) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} = \overrightarrow {CD} \)
c) Nếu có \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thì tứ giác ABCD là hình bình hành
d) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
Sử dụng quy tắc cộng vecto, lý thuyết các vecto bằng nhau, vecto đối nhau, quy tắc hình bình hành.
a) Sai . \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \) chưa phải là điều kiện đủ để tứ giác ABCD là hình bình hành.
b) Sai. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} = \overrightarrow {DC} \).
c) Đúng. Vì \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \Leftrightarrow \overrightarrow {SA} + \overrightarrow {AB} + \overrightarrow {SA} + \overrightarrow {AD} = \overrightarrow {SA} + \overrightarrow {SA} + \overrightarrow {AC} \)
\( \Leftrightarrow \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) suy ra ABCD là hình bình hành (theo quy tắc hình bình hành).
d) Sai. Vì tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
Trong không gian Oxyz, cho vecto \(\overrightarrow c = (3;4;0)\), \(\overrightarrow b = (1; - 2;2)\).
a) \(\left| {\overrightarrow a } \right| = 5\)
b) \(\overrightarrow c + \overrightarrow d = (4;2;2)\)
c) \(\overrightarrow c .\overrightarrow d = 1\)
d) Góc giữa hai vecto \(\overrightarrow c ,\overrightarrow d \) bằng \({90^o}\)
a) \(\left| {\overrightarrow a } \right| = 5\)
b) \(\overrightarrow c + \overrightarrow d = (4;2;2)\)
c) \(\overrightarrow c .\overrightarrow d = 1\)
d) Góc giữa hai vecto \(\overrightarrow c ,\overrightarrow d \) bằng \({90^o}\)
Sử dụng các quy tắc cộng vecto, công thức tính tích vô hướng của hai vecto, độ dài vecto, góc giữa hai vecto.
a) Đúng. Vì \(\left| {\overrightarrow a } \right| = \sqrt {{3^2} + {4^2} + {0^2}} = 5\).
b) Đúng. Vì \(\overrightarrow a + \overrightarrow b = (3 + 1;4 - 2;0 + 2) = (4;2;2)\).
c) Sai. Vì \(\overrightarrow a .\overrightarrow b = 3.1 + 4.( - 2) + 0.2 = - 5\) .
d) Sai. Vì \(\cos \left( {\overrightarrow c ,\overrightarrow d } \right) = \frac{{\overrightarrow c .\overrightarrow d }}{{\left| {\overrightarrow c } \right|.\left| {\overrightarrow d } \right|}} = \frac{{ - 5}}{{\sqrt {{3^2} + {4^2} + {0^2}} .\sqrt {{1^2} + {{( - 2)}^2} + {2^2}} }} = \frac{{ - 1}}{3}\) nên góc giữa hai vecto \(\overrightarrow c ,\overrightarrow d \) bằng xấp xỉ \({109^o}\).
Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = x\sqrt {1 - {x^2}} \) lần lượt là M, m. Tính M + m.
Đáp án:
Đáp án:
- Tính y’, tìm các nghiệm của y’ = 0.
- Tìm giá trị y tại các điểm cực trị của hàm số và hai đầu mút của đoạn.
Tập xác định: D = [-1;1].
Ta có: \[f'(x) = \sqrt {1 - {x^2}} - \frac{{{x^2}}}{{\sqrt {1 - {x^2}} }} = \frac{{1 - 2{x^2}}}{{\sqrt {1 - {x^2}} }} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{ - \sqrt 2 }}{2}}\\{x = \frac{{\sqrt 2 }}{2}}\end{array}} \right.\]
f(-1) = f(1) = 0; \(f\left( {\frac{{ - \sqrt 2 }}{2}} \right) = \frac{{ - 1}}{2}\); \(f\left( {\frac{{\sqrt 2 }}{2}} \right) = \frac{1}{2}\).
Vậy \(M + m = \frac{1}{2} + \frac{{ - 1}}{2} = 0\).
Tính tổng tất cả các giá trị thực của tham số m để đồ thị hàm số \(y = \frac{{{x^2} + m}}{{{x^2} - 3x + 2}}\) có đúng 2 đường tiệm cận.
Đáp án:
Đáp án:
Sử dụng quy tắc tìm đường tiệm cận của hàm phân thức.
Ta luôn có một đường tiệm cận ngang y = 1.
Đồ thị hàm số có đúng 2 đường tiệm cận khi và chỉ khi \({x^2} + m = 0\) có nghiệm x = 1 hoặc x = 2.
Khi x = 1 thì m = -1. Khi x = 2 thì m = -4. Vậy tổng các giá trị của m là -1 + (-4) = -5.
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết A(2;4;0), B(4;0;0), C(-1;4;-7) và D’(6;8;10). Tổng hoành độ, tung độ, cao độ của điểm B’ bằng bao nhiêu?
Đáp án:
Đáp án:
Tìm giao điểm O của AC và BD, từ đó tìm được D. Thông qua \(\overrightarrow {BB'} = \overrightarrow {DD'} \) ta tìm được tọa độ B’.
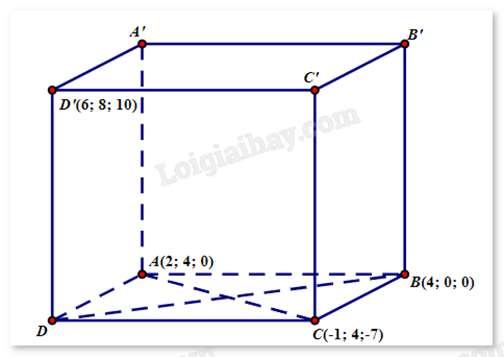
Giả sử D(a;b;c), B’(a’;b’;c’). Gọi O là giao điểm của AC và BD, suy ra O là trung điểm của AC.
Từ đó, ta tính được tọa độ điểm O\(\left( {\frac{1}{2};4;\frac{{ - 7}}{2}} \right)\).
Vì O là trung điểm của BD nên từ B(4;0;0) ta tìm được D(-3;8;-7).
Vậy, \(\overrightarrow {DD'} = (9;0;17)\). Mà ABCD.A’B’C’D’ là hình hộp nên \(\overrightarrow {BB'} = \overrightarrow {DD'} = (9;0;17)\).
Mà \(\overrightarrow {BB'} = (a' - 4;b';c')\), suy ra a’ = 13, b’ = 0, c’ = 17.
Vậy B’(13;0;17). Tổng hoành độ, tung độ, cao độ của điểm B’ bằng 13 + 0 + 17 = 30.
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G(x) = 0,035{x^2}(15 - x)\), trong đó x là liều lượng thuốc được tiêm cho bệnh nhân (x được tính bằng milligram). Tính liều lượng thuốc cần tiêm (đơn vị milligram) cho bệnh nhân để huyết áp giảm nhiều nhất.
Đáp án:
Đáp án:
Lập bảng biến thiên và tìm giá trị lớn nhất của hàm số.
Xét G(x) trên đoạn [0;15].
Ta có: \(G(x) = 0,035(15{x^2} - {x^3}) \Rightarrow G'(x) = 0,035(30x - 3{x^2})\).
\(G'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 10}\end{array}} \right.\)
Mặt khác, G(15) = 0; G(10) = 17,5; G(15) = 0. Vậy x cần tìm là 10.
Giá trị của tham số m để đồ thị hàm số \(y = {x^3} - 3{x^2} + m\) có hai điểm cực trị A, B thỏa mãn OA = OB (O là gốc tọa độ) có dạng \(\frac{a}{b}\) là một phân số tối giản. Tính a + b.
Đáp án:
Đáp án:
Tìm tọa điểm cực trị A, B của hàm số theo tham số m. Từ biểu thức độ dài OA = OB, tìm m.
Tập xác định: D = R.
\(y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
Do đó, đồ thị hàm số đã cho luôn có 2 điểm cực trị lần lượt có tọa độ là A(0; m) và B(2; -4 + m).
Ta có: \(OA = OB \Leftrightarrow \sqrt {{0^2} + {m^2}} = \sqrt {{2^2} + {{(4 - m)}^2}} \Leftrightarrow {m^2} = 4 + {(4 - m)^2}\)
\( \Leftrightarrow 20 - 8m = 0 \Leftrightarrow m = \frac{5}{2}\).
Vậy a = 5, b = 2. Suy ra a + b = 5 + 2 = 7.
Cho hàm số y = f(x) có đồ thị như hình:

Tìm số điểm cực trị của hàm số \(g(x) = f({x^2} - 3)\).
Đáp án:
Đáp án:
Tìm số nghiệm bội lẻ của phương trình g’(x) = 0.
Ta có: \(g'(x) = [f({x^2} - 3)]' = ({x^2} - 3)'f'({x^2} - 3) = 2xf'({x^2} - 3)\).
\(g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{{20}{c}}{2x = 0}\\{f'({x^2} - 3) = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{{20}{c}}{x = 0}\\{{x^2} - 3 = - 2}\\{{x^2} - 3 = 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{{20}{c}}{x = 0}\\{x = \pm 1}\\{x = \pm 2}\end{array}} \right.} \right.\)
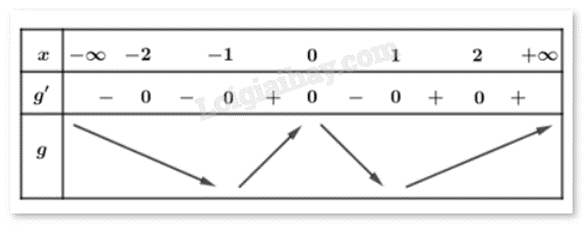
Vì f’(x) không đổi dấu khi qua x = 1 nên g(x) có 3 điểm cực trị.