Trắc nghiệm Bài 2: Tam giác bằng nhau Toán 7 Chân trời sáng tạo
Đề bài
Cho \(\Delta ABC = \Delta DEF.\) Cho \(\widehat E = 46^\circ \). Khẳng định đúng là:
-
A.
\(\widehat A = 46^\circ \)
-
B.
\(\widehat B = 46^\circ \)
-
C.
\(\widehat F = 46^\circ \)
-
D.
\(\widehat C = 46^\circ \)
Cho \(\Delta ABC = \Delta MNP.\) Biết AC = 6 cm, NP = 8 cm và chu vi của tam giác MNP bằng 22cm. Tìm khẳng định sai:
-
A.
MP = 8 cm
-
B.
BC = 8 cm
-
C.
MN = 8 cm
-
D.
AB = 8 cm
-
A.
\(AD//BC\)
-
B.
\(AB//CD\)
-
C.
\(\Delta ABC = \Delta CDA\)
-
D.
\(\Delta ABC = \Delta ADC\)
-
A.
Tam giác ABC
-
B.
Tam giác CBA
-
C.
Tam giác DBA
-
D.
Tam giác BCA
Cho \(\Delta\)ABC có AB = AC và MB = MC (\(M \in BC\)).Chọn câu sai.
-
A.
\(\Delta AMC = \Delta BCM\)
-
B.
\(AM \bot BC\)
-
C.
\(\widehat {BAM} = \widehat {CAM}\)
-
D.
\(\Delta AMB = \Delta AMC\)
Cho tam giác \(MNP\) có MN = MP. Gọi \(A\) là trung điểm của \(NP.\) Biết \(\widehat {NMA} = {20^0}\) thì số đo góc \(MPN\) là:
-
A.
50\(^\circ \)
-
B.
40\(^\circ \)
-
C.
70\(^\circ \)
-
D.
80\(^\circ \)
Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A + \widehat B = {130^0},\widehat E = {55^0}.\) Tính các góc \(\widehat A,\widehat C,\widehat D,\widehat F.\)
-
A.
\(\widehat A = \widehat D = 65^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\)
-
B.
\(\widehat A = \widehat D = 50^\circ ;\,\widehat C\, = \widehat F = 65^\circ .\)
-
C.
\(\widehat A = \widehat D = 75^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\)
-
D.
\(\widehat A = \widehat D = 50^\circ ;\,\widehat C\, = \widehat F = 75^\circ .\)
Cho \(\widehat {xOy} = {50^0}\), vẽ cung tròn tâm O bán kính bằng 2cm, cung tròn này cắt Ox, Oy lần lượt ở A và B. Vẽ các cung tròn tâm A và tâm B có bán kính 3cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính \(\widehat {xOC}\) .
-
A.
\({40^0}\)
-
B.
\({25^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
-
A.
\(\Delta ABC = \Delta DEA\)
-
B.
\(\widehat D = \widehat A\)
-
C.
\(\widehat E = \widehat B\)
-
D.
\(\widehat C = \widehat E\)
Cho tam giác \(ABC\) có \(AB < AC\) . Gọi \(E \in AC\) sao cho \(AB = CE\). Gọi \(O\) là một điểm nằm ở trong tam giác sao cho \(OA = OC,OB = OE.\) Khi đó:
-
A.
\(\Delta AOB = \Delta CEO\)
-
B.
\(\Delta AOB = \Delta COE\)
-
C.
\(\widehat {AOB} = \widehat {OEC}\)
-
D.
\(\widehat {ABO} = \widehat {OCE}\)
Cho tam giác \(BAC\) và tam giác \(KEF\) có \(BA = EK,\) \(\widehat A = \widehat K\), \(CA = KF.\) Phát biểu nào trong trong các phát biểu sau đây là đúng:
-
A.
\(\Delta BAC = \Delta EKF\)
-
B.
\(\Delta BAC = \Delta EFK\)
-
C.
\(\Delta {\rm A}BC = \Delta FKE\)
-
D.
\(\Delta BAC = \Delta KEF\)
Cho tam giác \(ABC\) và tam giác \(MNP\) có \(\widehat A = \widehat {M,}\widehat B = \widehat N\) . Cần thêm điều kiện gì để tam giác \(ABC\) và tam giác \(MNP\) bằng nhau theo trường hợp góc – cạnh – góc:
-
A.
\(AC = MP\)
-
B.
\(AB = MN\)
-
C.
\(BC = NP\)
-
D.
\(AC = MN\)
Cho góc nhọn \(xOy,Oz\) là tia phân giác của góc đó. Qua điểm \(A\) thuộc tia \(Ox\) kẻ đường thẳng song song với \(Oy\) cắt \(Oz\) ở \(M.\) Qua \(M\)kẻ đường thẳng song song với \(Ox\) cắt \(Oy\) ở \(B.\) Chọn câu đúng.
-
A.
\(OA > OB;MA > MB\)
-
B.
\(OA = OB;MA = MB\)
-
C.
\(OA < OB;MA < MB\)
-
D.
\(OA < OB;MA = MB\)
Cho hai đoạn thẳng \(BD\) và \(EC\) vuông góc với nhau tại \(A\) sao cho \(AB = AE,AD = AC,AB < AC.\) Phát biểu nào trong các phát biểu sau đây là sai:
-
A.
\(\Delta AED = \Delta ABC\)
-
B.
\(BC = ED\)
-
C.
\(EB = CD\)
-
D.
\(\widehat {ABC} = \widehat {AED}\) .
Cho góc nhọn \(xOy.\) Trên tia \(Ox\) lấy hai điểm \(A,C,\) trên tia \(Oy\) lấy hai điểm \(B,D\) sao cho \(OA = OB,OC = OD\) (\(A\) nằm giữa \(O\) và \(C,\)\(B\) nằm giữa \(O\) và \(D\) ). So sánh hai góc \(\widehat {CAD}\) và \(\widehat {CBD}.\)
-
A.
\(\widehat {CBD} = \widehat {CAD}\)
-
B.
\(\widehat {CBD} < \widehat {CAD}\)
-
C.
\(\widehat {CBD} > \widehat {CAD}\)
-
D.
\(2.\widehat {CBD} = \widehat {CAD}\)
Cho tam giác \(ABC\) có \(AB = AC = BC,\) phân giác \(BD\) và \(CE\) cắt nhau tại \(O.\) Tính \(\widehat {BOC}.\)
-
A.
\({60^0}\)
-
B.
\({80^0}\)
-
C.
\(120^\circ \)
-
D.
\({100^0}\)
Cho hai đoạn thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) là trung điểm của mỗi đoạn thẳng đó. Lấy \(E;\,F\) lần lượt là điểm thuộc đoạn \(AD\) và \(BC\) sao cho \(AE = BF.\) Cho \(OE = 2cm\), tính \(EF.\)
-
A.
\(4\,cm\)
-
B.
\(2cm\)
-
C.
\(3\,cm\)
-
D.
\(3,5\,cm\)
Cho tam giác \(ABC\) có \(AB = AC.\) Trên các cạnh \(AB\) và \(AC\) lấy các điểm \(D,E\) sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của \(BE\) và \(CD\). Chọn câu sai.
-
A.
\(BE = CD\)
-
B.
\(BK = KC\)
-
C.
\(BD = CE\)
-
D.
\(DK = KC\)
Cho tam giác \(DEF\) và tam giác \(HKG\) có \(\widehat D = \widehat H\), \(\widehat E = \widehat K\), \(DE = HK.\) Biết \(\widehat F = {80^0}\). Số đo góc \(G\) là:
-
A.
\({70^0}\)
-
B.
\({80^0}\)
-
C.
\({90^0}\)
-
D.
\({100^0}\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = AC.\) Qua \(A\) kẻ đường thẳng \(xy\) sao cho \(B,C\) nằm cùng phía với \(xy.\) Kẻ \(BD\) và \(CE\) vuông góc với \(xy.\) Chọn câu đúng.
-
A.
\(DE = BD + CE\)
-
B.
\(DE = BD - CE\)
-
C.
\(CE = BD + DE\)
-
D.
\(CE = BD - DE\)
Lời giải và đáp án
Cho \(\Delta ABC = \Delta DEF.\) Cho \(\widehat E = 46^\circ \). Khẳng định đúng là:
-
A.
\(\widehat A = 46^\circ \)
-
B.
\(\widehat B = 46^\circ \)
-
C.
\(\widehat F = 46^\circ \)
-
D.
\(\widehat C = 46^\circ \)
Đáp án : B
Khi 2 tam giác bằng nhau thì các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Vì \(\Delta ABC = \Delta DEF.\)
\( \Rightarrow \) ( 2 góc tương ứng)
\( \Rightarrow \widehat B = 46^\circ \)
Cho \(\Delta ABC = \Delta MNP.\) Biết AC = 6 cm, NP = 8 cm và chu vi của tam giác MNP bằng 22cm. Tìm khẳng định sai:
-
A.
MP = 8 cm
-
B.
BC = 8 cm
-
C.
MN = 8 cm
-
D.
AB = 8 cm
Đáp án : A
Khi 2 tam giác bằng nhau thì các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau
Chu vi tam giác bằng tổng độ dài 3 cạnh
Vì \(\Delta ABC = \Delta MNP.\)
\( \Rightarrow \) AB = MN, BC = NP; AC = MP
Mà AC = 6 cm, NP = 8 cm
Nên MP = 6 cm, BC = 8 cm
Chu vi của tam giác MNP bằng 22cm nên MN + NP + MP = 22 cm hay MN + 8 + 6 = 22 cm nên MN = 8 cm
Do đó, AB = MN = 8 cm
Vậy các khẳng định B,C,D là đúng; khẳng định A sai.
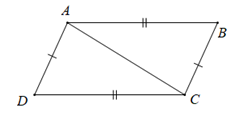
-
A.
\(AD//BC\)
-
B.
\(AB//CD\)
-
C.
\(\Delta ABC = \Delta CDA\)
-
D.
\(\Delta ABC = \Delta ADC\)
Đáp án : D
2 tam giác có 3 cặp cạnh tương ứng bằng nhau thì 2 tam giác đó bằng nhau. ( c.c.c)
Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
Xét tam giác \(ADC\) và \(CBA\) có
\(AB = CD\)
\(AD = BC\)
\(DB\) chung
\( \Rightarrow \Delta ADC = CBA\left( {c.c.c} \right)\)
Do đó \(\widehat {DAC} = \widehat {BCA}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong nên \(AD//BC.\)
Tương tự ta có \(AB//DC.\)
Vậy A, B, C đúng, D sai.
-
A.
Tam giác ABC
-
B.
Tam giác CBA
-
C.
Tam giác DBA
-
D.
Tam giác BCA
Đáp án : B
2 tam giác có 3 cặp cạnh tương ứng bằng nhau thì 2 tam giác đó bằng nhau. ( c.c.c)
Xét tam giác DEA và tam giác CBA, ta có:
DE = CB
EA = BA
DA = CA
\( \Rightarrow \Delta DEA = \Delta CBA\) ( c.c.c)
Cho \(\Delta\)ABC có AB = AC và MB = MC (\(M \in BC\)).Chọn câu sai.
-
A.
\(\Delta AMC = \Delta BCM\)
-
B.
\(AM \bot BC\)
-
C.
\(\widehat {BAM} = \widehat {CAM}\)
-
D.
\(\Delta AMB = \Delta AMC\)
Đáp án : A
2 tam giác có 3 cặp cạnh tương ứng bằng nhau thì 2 tam giác đó bằng nhau. ( c.c.c)
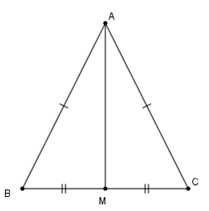
Xét \(\Delta AMB\) và \(\Delta AMC\) có
\(AB = AC\,\left( {gt} \right)\)
\(MB = MC\left( {gt} \right)\)
Cạnh \(AM\) chung
Nên \(\Delta AMB = \Delta AMC\,\left( {c - c - c} \right)\)
Suy ra \(\widehat {BAM} = \widehat {CAM}\) và \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng bằng nhau)
Mà \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {AMB} = \widehat {AMC} = \frac{{180^\circ }}{2} = 90^\circ .\) Hay \(AM \bot BC.\)
Vậy B, C, D đúng, A sai.
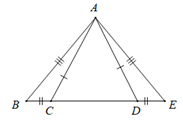
Cho tam giác \(MNP\) có MN = MP. Gọi \(A\) là trung điểm của \(NP.\) Biết \(\widehat {NMA} = {20^0}\) thì số đo góc \(MPN\) là:
-
A.
50\(^\circ \)
-
B.
40\(^\circ \)
-
C.
70\(^\circ \)
-
D.
80\(^\circ \)
Đáp án : C
+ Áp dụng tính chất hai tam giác bằng nhau suy ra các cặp góc tương ứng bằng nhau.
+ Áp dụng định lý tổng ba góc trong tam giác, tìm góc chưa biết số đo trong tam giác.

Xét tam giác \(NAM\) và tam giác \(PAM\) có:
\(MN = MP,\) \(NA = PA,\) \(MA\) là cạnh chung.
Do đó \(\Delta NAM = \Delta PAM\,\left( {c - c - c} \right).\)
Nên \(\widehat {ANM} = \widehat {APM}\) ; \(\widehat {NMA} = \widehat {PMA}\) (hai góc tương ứng)
Do đó\(\widehat {NMP} = \widehat {NMA} + \widehat {PMA} = 20^\circ + 20^\circ = 40^\circ \)
Áp dụng định lý tổng 3 góc trong tam giác \(MNP\) có:
\(\widehat {NMP} + \widehat {MPN} + \widehat {PNM} = {180^0} \Rightarrow 2\widehat {MPN} + \widehat {NMP} = {180^0}\)
\(\widehat {MPN} = \left( {{{180}^0} - \widehat {NMP}} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.\)
Cho \(\Delta ABC = \Delta DEF.\) Biết \(\widehat A + \widehat B = {130^0},\widehat E = {55^0}.\) Tính các góc \(\widehat A,\widehat C,\widehat D,\widehat F.\)
-
A.
\(\widehat A = \widehat D = 65^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\)
-
B.
\(\widehat A = \widehat D = 50^\circ ;\,\widehat C\, = \widehat F = 65^\circ .\)
-
C.
\(\widehat A = \widehat D = 75^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\)
-
D.
\(\widehat A = \widehat D = 50^\circ ;\,\widehat C\, = \widehat F = 75^\circ .\)
Đáp án : C
+ Áp dụng tính chất hai tam giác bằng nhau suy ra các cặp góc tương ứng bằng nhau.
+ Áp dụng định lý tổng ba góc trong tam giác, tìm góc chưa biết số đo trong tam giác.
Vì \(\Delta ABC = \Delta DEF\) nên \(\widehat A = \widehat D;\,\widehat B = \widehat E = 55^\circ ;\widehat C\, = \widehat F.\) ( các góc tương ứng)
Xét tam giác \(ABC\) có \(\widehat A + \widehat B = 130^\circ \Rightarrow \widehat A = 130^\circ - \widehat B\) \( = 130^\circ - 55^\circ = 75^\circ \)
Lại có \(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right)\) \( = 180^\circ - 130^\circ = 50^\circ .\)
Vậy \(\widehat A = \widehat D = 75^\circ ;\,\widehat C\, = \widehat F = 50^\circ .\)
Cho \(\widehat {xOy} = {50^0}\), vẽ cung tròn tâm O bán kính bằng 2cm, cung tròn này cắt Ox, Oy lần lượt ở A và B. Vẽ các cung tròn tâm A và tâm B có bán kính 3cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính \(\widehat {xOC}\) .
-
A.
\({40^0}\)
-
B.
\({25^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Đáp án : B
Ta chứng minh hai tam giác bằng nhau để suy ra hai góc tương ứng bằng nhau
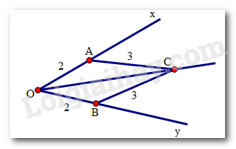
Xét hai tam giác OAC và OBC có:
OA = OB (= 2cm)
OC chung
AC = BC (= 3cm)
Nên \(\Delta OAC = \Delta OBC(c.c.c)\)
Do đó \(\widehat {AOC} = \widehat {COB}\) (hai góc tương ứng).
Mà \(\widehat {AOC} + \widehat {COB} = {50^0}\) nên \(\widehat {AOC} = \widehat {COB} = \frac{{{{50}^0}}}{2} = {25^0}\)
Vậy \(\widehat {xOC} = {25^0}\).
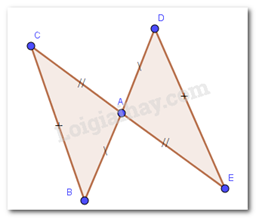
-
A.
\(\Delta ABC = \Delta DEA\)
-
B.
\(\widehat D = \widehat A\)
-
C.
\(\widehat E = \widehat B\)
-
D.
\(\widehat C = \widehat E\)
Đáp án : D
2 tam giác có 3 cặp cạnh tương ứng bằng nhau thì 2 tam giác đó bằng nhau. ( c.c.c)
Áp dụng tính chất hai tam giác bằng nhau suy ra các cặp góc tương ứng bằng nhau.
Xét \(\Delta \)ABC và \(\Delta \)ADE, ta có:
AB = AD
BC = DE
AC = AE
\( \Rightarrow \Delta ABC = \Delta ADE\) ( c.c.c)
\( \Rightarrow \widehat {BAC} = \widehat {DAE};\widehat B = \widehat D;\widehat C = \widehat E\) ( các góc tương ứng)
Cho tam giác \(ABC\) có \(AB < AC\) . Gọi \(E \in AC\) sao cho \(AB = CE\). Gọi \(O\) là một điểm nằm ở trong tam giác sao cho \(OA = OC,OB = OE.\) Khi đó:
-
A.
\(\Delta AOB = \Delta CEO\)
-
B.
\(\Delta AOB = \Delta COE\)
-
C.
\(\widehat {AOB} = \widehat {OEC}\)
-
D.
\(\widehat {ABO} = \widehat {OCE}\)
Đáp án : B
2 tam giác có 3 cặp cạnh tương ứng bằng nhau thì 2 tam giác đó bằng nhau. ( c.c.c)
Áp dụng tính chất hai tam giác bằng nhau suy ra các cặp góc tương ứng bằng nhau.
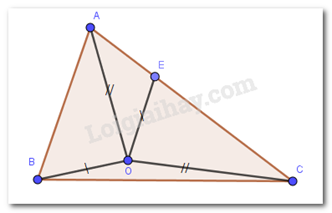
Xét tam giác \(AOB\) và tam giác \(COE\) có:
\(AB = CE\left( {gt} \right);AO = CO;OB = OE\)
Do đó: \(\Delta AOB = \Delta COE(c.c.c)\) suy ra \(\widehat {AOB} = \widehat {COE};\,\widehat {ABO} = \widehat {OEC}\) (hai góc tương ứng bằng nhau)
Nên A, C, D sai, B đúng.
Cho tam giác \(BAC\) và tam giác \(KEF\) có \(BA = EK,\) \(\widehat A = \widehat K\), \(CA = KF.\) Phát biểu nào trong trong các phát biểu sau đây là đúng:
-
A.
\(\Delta BAC = \Delta EKF\)
-
B.
\(\Delta BAC = \Delta EFK\)
-
C.
\(\Delta {\rm A}BC = \Delta FKE\)
-
D.
\(\Delta BAC = \Delta KEF\)
Đáp án : A
Sử dụng trường hợp bằng nhau thứ hai của tam giác
Xét tam giác \(BAC\) và tam giác \(KEF\) có \(BA = EK,\) \(\widehat A = \widehat K\), \(CA = KF.\) suy ra \(\Delta BAC = \Delta EKF\)(c.g.c)
Cho tam giác \(ABC\) và tam giác \(MNP\) có \(\widehat A = \widehat {M,}\widehat B = \widehat N\) . Cần thêm điều kiện gì để tam giác \(ABC\) và tam giác \(MNP\) bằng nhau theo trường hợp góc – cạnh – góc:
-
A.
\(AC = MP\)
-
B.
\(AB = MN\)
-
C.
\(BC = NP\)
-
D.
\(AC = MN\)
Đáp án : B
Áp dụng trường hợp bằng nhau thứ ba của tam giác.
Ta thấy hai tam giác \(ABC\) và tam giác \(MNP\) có hai yếu tố về góc \(\widehat A = \widehat {M,}\widehat B = \widehat N\).
Để tam giác \(ABC\) và tam giác \(MNP\) bằng nhau theo trường hợp góc – cạnh – góc thì cần thêm điều kiện về cạnh kề hai góc đã cho đó là \(AB = MN.\)
Cho góc nhọn \(xOy,Oz\) là tia phân giác của góc đó. Qua điểm \(A\) thuộc tia \(Ox\) kẻ đường thẳng song song với \(Oy\) cắt \(Oz\) ở \(M.\) Qua \(M\)kẻ đường thẳng song song với \(Ox\) cắt \(Oy\) ở \(B.\) Chọn câu đúng.
-
A.
\(OA > OB;MA > MB\)
-
B.
\(OA = OB;MA = MB\)
-
C.
\(OA < OB;MA < MB\)
-
D.
\(OA < OB;MA = MB\)
Đáp án : B
+ Từ tính chất đường thẳng song song, tính chất tia phân giác suy ra các cặp góc bằng nhau.
+ Dựa vào trường hợp bằng nhau thứ ba của tam giác và hệ quả của trường hợp bằng nhau thứ ba để chứng minh các tam giác bằng nhau để suy ra các cặp cạnh bằng nhau.

Ta có:
\(\widehat {{M_1}} = \widehat {{O_2}}\) (hai góc so le trong)
\(\widehat {{M_2}} = \widehat {{O_1}}\) (hai góc so le trong)
\(\widehat {{O_2}} = \widehat {{O_1}}\)(do Oz là tia phân giác của góc xOy)
Do đó \(\widehat {{M_2}} = \widehat {{M_1}}\)
Xét tam giác \(AOM\) và tam giác \(BOM\) có:
\(\widehat {{M_2}} = \widehat {{M_1}}\)(cmt)
\(OM\) là cạnh chung
\(\widehat {{O_2}} = \widehat {{O_1}}\)(cmt)
\( \Rightarrow \Delta AOM = \Delta BOM(g.c.g)\)
Do đó \(OA = OB;MA = MB\) (các cặp cạnh tương ứng).
Cho hai đoạn thẳng \(BD\) và \(EC\) vuông góc với nhau tại \(A\) sao cho \(AB = AE,AD = AC,AB < AC.\) Phát biểu nào trong các phát biểu sau đây là sai:
-
A.
\(\Delta AED = \Delta ABC\)
-
B.
\(BC = ED\)
-
C.
\(EB = CD\)
-
D.
\(\widehat {ABC} = \widehat {AED}\) .
Đáp án : C
+ Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh hai tam giác bằng nhau.
+ Sử dụng tính chất của hai tam giác bằng nhau để suy ra các tính chất về cạnh, về góc tương ứng.

Xét hai tam giác \(ABC\) và tam giác \(AED\) có:
\(AB = AB;\) \(\widehat {BAD} = \widehat {BAC}\)(hai góc đối đỉnh); \(AD = DC,\)
\( \Rightarrow \)\(\Delta AED = \Delta ABC\) (A đúng).
\( \Rightarrow \) \(BC = BD\) (hai cạnh tương ứng) (B đúng);
\(\widehat {ABC} = \widehat {ABD}\)(hai góc tương ứng) (D đúng).
Cho góc nhọn \(xOy.\) Trên tia \(Ox\) lấy hai điểm \(A,C,\) trên tia \(Oy\) lấy hai điểm \(B,D\) sao cho \(OA = OB,OC = OD\) (\(A\) nằm giữa \(O\) và \(C,\)\(B\) nằm giữa \(O\) và \(D\) ). So sánh hai góc \(\widehat {CAD}\) và \(\widehat {CBD}.\)
-
A.
\(\widehat {CBD} = \widehat {CAD}\)
-
B.
\(\widehat {CBD} < \widehat {CAD}\)
-
C.
\(\widehat {CBD} > \widehat {CAD}\)
-
D.
\(2.\widehat {CBD} = \widehat {CAD}\)
Đáp án : A
+ Sử dụng tính chất hai tam giác bằng nhau ở ý trước suy ra hai góc tương ứng bằng nhau
+ Sau đó sử dụng tính chất hai góc kề bù hoặc góc ngoài để so sánh hai góc \(\widehat {CAD}\) và \(\widehat {CBD}.\)
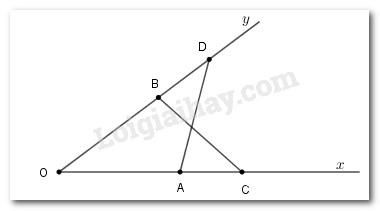
Xét tam giác \(OAD\) và tam giác \(OBC\) có
\(OA = OB,\)
\(\widehat O\)chung,
\(OC = OD\)
\( \Rightarrow \)\(\Delta OAD = \Delta OBC\) ( c.g.c)
\( \Rightarrow \)\(\widehat {OBC} = \widehat {OAD}\) (hai góc tương ứng bằng nhau)
Lại có \(\widehat {OBC} + \widehat {CBD} = 180^\circ ;\,\widehat {OAD} + \widehat {DAC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {CBD} = 180^\circ - \widehat {OBC}\) và \(\widehat {CAD} = 180^\circ - \widehat {OAD}\) mà \(\widehat {OBC} = \widehat {OAD}\) (cmt)
\( \Rightarrow \) \(\widehat {CBD} = \widehat {CAD}.\)
Cho tam giác \(ABC\) có \(AB = AC = BC,\) phân giác \(BD\) và \(CE\) cắt nhau tại \(O.\) Tính \(\widehat {BOC}.\)
-
A.
\({60^0}\)
-
B.
\({80^0}\)
-
C.
\(120^\circ \)
-
D.
\({100^0}\)
Đáp án : C
Sử dụng tính chất tia phân giác, tính chất hai góc kề bù và định lý tổng ba góc trong tam giác.
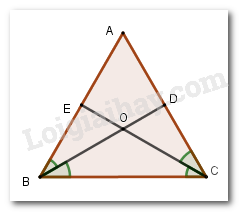
Vì \(BD\) và \(CE\) là tia phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) nên \(\widehat {ABD} = \widehat {CBD}\) và \(\widehat {ACE} = \widehat {BCE}.\)
Xét tam giác \(ABD\) và tam giác \(CBD\) có:
+ \(AB = AC\,\left( {gt} \right)\)
+ \(\widehat {ABD} = \widehat {CBD}\) (cmt)
+ Cạnh \(BD\) chung
Suy ra \(\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)\)\( \Rightarrow \widehat {BCA} = \widehat {BAC}\) (hai góc tương ứng) (1)
Tương tự ta có \(\Delta BCE = \Delta ACE\left( {c - g - c} \right)\) \( \Rightarrow \widehat {CBA} = \widehat {BAC}\) (hai góc tương ứng) (2)
Từ (1) và (2) ta có \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB}\). Mà \(\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ \) (định lý tổng ba góc của tam giác) nên \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB} = \frac{{180^\circ }}{3} = 60^\circ .\)
Lại có \(\widehat {ABD} = \widehat {CBD}\) (cmt) nên \(\widehat {CBO} = \frac{{\widehat {ABC}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \); \(\widehat {ACE} = \widehat {BCE} = \frac{{\widehat {ACB}}}{2} = \frac{{60^\circ }}{2} = 30^\circ .\)
Xét tam giác \(BOC\) có \(\widehat {BOC} + \widehat {OBC} + \widehat {OCB} = 180^\circ \) (định lý tổng ba góc của một tam giác)
Nên \(\widehat {BOC} = 180^\circ - 30^\circ - 30^\circ = 120^\circ .\)
Vậy \(\widehat {BOC} = 120^\circ .\)
Cho hai đoạn thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) là trung điểm của mỗi đoạn thẳng đó. Lấy \(E;\,F\) lần lượt là điểm thuộc đoạn \(AD\) và \(BC\) sao cho \(AE = BF.\) Cho \(OE = 2cm\), tính \(EF.\)
-
A.
\(4\,cm\)
-
B.
\(2cm\)
-
C.
\(3\,cm\)
-
D.
\(3,5\,cm\)
Đáp án : A
Dùng trường hợp bằng nhau thứ hai để chứng minh hai tam giác bằng nhau, từ đó có các cạnh và các góc tương ứng. Lập luận để có được \(O\) là trung điểm của \(EF\) để tính độ dài \(EF.\)
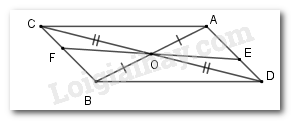
* Xét tam giác \(OBC\) và \(OAD\) có
+ \(OA = OB\,\left( {gt} \right)\)
+ \(\widehat {AOD} = \widehat {BOC}\) (đối đỉnh)
+ \(OC = OD\left( {gt} \right)\)
\( \Rightarrow \)\(\Delta OAD = \Delta OBC\left( {c - g - c} \right)\) nên \(\widehat {OAD} = \widehat {OBC}\) (hai góc tương ứng)
* Xét tam giác \(OBF\) và \(OAE\) có
+ \(OA = OB\,\left( {gt} \right)\)
+ \(\widehat {OAD} = \widehat {OBC}\) (cmt)
+ \(BF = AE\left( {gt} \right)\)
\( \Rightarrow \)\(\Delta OBF = \Delta OAE\left( {c - g - c} \right)\)
\( \Rightarrow \)\(OE = OF\) (hai cạnh tương ứng) và \(\widehat {AOE} = \widehat {FOB}\) (hai góc tương ứng)
Mà \(\widehat {FOB} + \widehat {FOA} = 180^\circ \) (hai góc kề bù) nên \(\widehat {FOA} + \widehat {AOE} = 180^\circ \)
\( \Rightarrow \) 3 điểm \(F;\,O;E\) thẳng hàng và \(OE = OF\) nên \(O\) là trung điểm của \(EF \Rightarrow EF = 2.OE = 4\,cm.\)
Cho tam giác \(ABC\) có \(AB = AC.\) Trên các cạnh \(AB\) và \(AC\) lấy các điểm \(D,E\) sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của \(BE\) và \(CD\). Chọn câu sai.
-
A.
\(BE = CD\)
-
B.
\(BK = KC\)
-
C.
\(BD = CE\)
-
D.
\(DK = KC\)
Đáp án : D
Chứng minh 2 tam giác bằng nhau rồi dựa vào tính chất hai tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau.
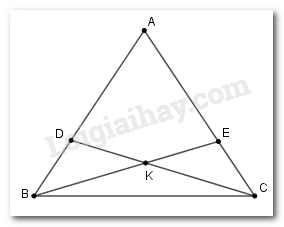
Xét tam giác \(ABE\) và tam giác \(ADC\) có
+ \(AD = AE\left( {gt} \right)\)
+ Góc \(A\) chung
+ \(AB = AC\left( {gt} \right)\)
\( \Rightarrow \) \(\Delta ABE = \Delta ACD\left( {c - g - c} \right)\)
\( \Rightarrow \widehat {ABE} = \widehat {ACD};\widehat {ADC} = \widehat {AEB}\) (hai góc tương ứng) và \(BE = CD\) (hai cạnh tương ứng) nên A đúng.
Lại có \(\widehat {ADC} + \widehat {BDC} = 180^\circ \); \(\widehat {AEB} + \widehat {BEC} = 180^\circ \) (hai góc kề bù) mà \(\widehat {ADC} = \widehat {AEB}\) (cmt)
\( \Rightarrow \)\(\widehat {BDC} = \widehat {BEC}.\)
Lại có \(AB = AC;\,AD = AE\left( {gt} \right)\) \( \Rightarrow AB - AD = AC - AE \Rightarrow BD = EC\) nên C đúng.
Xét tam giác \(KBD\) và tam giác \(KCE\) có
\(\widehat {ABE} = \widehat {ACD}\,\left( {cmt} \right)\)
\(BD = EC\,\left( {cmt} \right)\)
\(\widehat {BDC} = \widehat {BEC}\,\left( {cmt} \right)\)
\( \Rightarrow \) \(\Delta KBD = \Delta KCE\left( {g - c - g} \right)\)
\( \Rightarrow KB = KC;\,KD = KE\) (hai cạnh tương ứng) nên B đúng, D sai.
Cho tam giác \(DEF\) và tam giác \(HKG\) có \(\widehat D = \widehat H\), \(\widehat E = \widehat K\), \(DE = HK.\) Biết \(\widehat F = {80^0}\). Số đo góc \(G\) là:
-
A.
\({70^0}\)
-
B.
\({80^0}\)
-
C.
\({90^0}\)
-
D.
\({100^0}\)
Đáp án : B
Áp dụng trường hợp bằng nhau thứ ba của tam giác để chứng minh hai tam giác bằng nhau, từ đó suy ra tính chất về góc của hai tam giác bằng nhau.
Xét tam giác \(DEF\) và tam giác \(HKG\) có \(\widehat D = \widehat H\), \(\widehat E = \widehat K\), \(DE = HK,\) do đó \(\Delta DEF = \Delta HKG\)(g.C.g).
Do đó \(\widehat G = \widehat F = {80^0}\) (hai góc tương ứng).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = AC.\) Qua \(A\) kẻ đường thẳng \(xy\) sao cho \(B,C\) nằm cùng phía với \(xy.\) Kẻ \(BD\) và \(CE\) vuông góc với \(xy.\) Chọn câu đúng.
-
A.
\(DE = BD + CE\)
-
B.
\(DE = BD - CE\)
-
C.
\(CE = BD + DE\)
-
D.
\(CE = BD - DE\)
Đáp án : A
+ Dựa vào hệ quả của trường hợp bằng nhau thứ ba của tam giác để chứng minh các cặp tam giác bằng nhau
+ Từ các cặp cạnh tương ứng bằng nhau ta lập luận để suy ra mối quan hệ đúng.
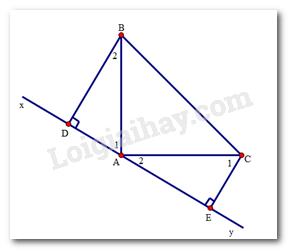
Ta có: \({\widehat A_1} + {\widehat A_2} = {90^0}\,\,\,\left( {do\,\,\,\widehat {BAC} = {{90}^0}} \right)\)
Mà \({\widehat A_1} + {\widehat B_2} = {90^0}\) (vì tam giác \(ABD\) vuông tại \(D.\))
\( \Rightarrow {\widehat B_2} = {\widehat A_2}\) (cùng phụ với \({\widehat A_1}\)).
Lại có \({\widehat A_2} + {\widehat C_1} = {90^0}\) (vì tam giác \(ACE\) vuông tại \(E\) )
\( \Rightarrow {\widehat A_1} = {\widehat C_1}\) (cùng phụ với \({\widehat A_2}\)).
Xét hai tam giác \(BDA\) và \(AEC\) có:
\(\widehat {{B_2}} = \widehat {{A_2}}\); \(AB = AC\) (gt) và\(\widehat {{A_1}} = \widehat {{C_1}}\) (cmt)
\( \Rightarrow \Delta BA{\rm{D}} = \Delta ACE\) (g.c.g)
\( \Rightarrow \) \(BD = AE\) (hai cạnh tương ứng), \(CE = AD\) (hai cạnh tương ứng).
Do đó \(DE = AD + AE = CE + BD.\)