Đề thi giữa kì 1 Toán 10 - Đề số 13
Phần trắc nghiệm
Đề bài
Câu nào sau đây là một mệnh đề?
-
A.
Số 30 có phải số chẵn không?
-
B.
Số 30 là số chẵn.
-
C.
2x – 1 là số lẻ.
-
D.
\({x^3} + 1 = 0\).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(x - {y^2} < 0\)
-
B.
\(x + y < 3xy\)
-
C.
\(x + \frac{1}{y} \ge 0\)
-
D.
\(\frac{x}{3} + \frac{y}{2} < 0\)
Cặp số nào sau đây là một nghiệm của bất phương trình \(x + 2y \le 4\)?
-
A.
\((2;1)\)
-
B.
\((1;2)\)
-
C.
\((1;3)\)
-
D.
\(( - 1;3)\)
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\) chứa điểm nào trong các điểm sau đây?
-
A.
\((0;0)\)
-
B.
\((1;0)\)
-
C.
\((0; - 2)\)
-
D.
\((0;2)\)
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB và \(\widehat A = {60^o}\). Đẳng thức nào sau đây đúng?
-
A.
\({a^2} = {b^2} + {c^2} - 3bc\)
-
B.
\({a^2} = {b^2} + {c^2} + bc\)
-
C.
\({a^2} = {b^2} + {c^2} + 3bc\)
-
D.
\({a^2} = {b^2} + {c^2} - bc\)
Cho các tập hợp \(A = \{ 0;2;4;6;8\} \) và \(B = \{ 1;2;3;4;5;6\} \). Tìm \(A\backslash B\).
-
A.
{0;8}
-
B.
{1;3;5}
-
C.
{0;2;8}
-
D.
{2;4;6}
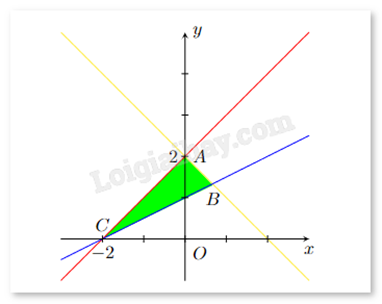
Miền tam giác (kể cả ba cạnh AB, BC, CA) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?
-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \ge 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \le 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \ge 0}\end{array}} \right.\)
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({180^o} - \alpha ) = - \sin \alpha \)
-
B.
\(\cos ({180^o} - \alpha ) = \cos \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Với \(x \in \mathbb{R}\), tìm mệnh đề đúng trong các mệnh đề sau.
-
A.
\(\forall x \in ( - \infty ;1] \Leftrightarrow x < 1\)
-
B.
\(\forall x \in ( - \infty ;1] \Leftrightarrow x \le 1\)
-
C.
\(\forall x \in ( - \infty ;1) \Leftrightarrow x \le 1\)
-
D.
\(\forall x \in ( - \infty ;1) \Leftrightarrow x < - 1\)
Tam giác ABC có AB = 6, AC = 9, \(\widehat A = {60^o}\). Tính diện tích tam giác ABC.
-
A.
\({S_{\Delta ABC}} = \frac{{27\sqrt 3 }}{2}\)
-
B.
\({S_{\Delta ABC}} = \frac{{27}}{2}\)
-
C.
\({S_{\Delta ABC}} = \frac{{27\sqrt 3 }}{4}\)
-
D.
\({S_{\Delta ABC}} = \frac{{27}}{4}\)
Cho tập hợp \(A = \{ 0;2;3;4;5\} \). Tập hợp nào sau đây là tập con của A?
-
A.
\(\{ 1;4\} \)
-
B.
\(\{ 3;8\} \)
-
C.
\(\{ 0;2;5\} \)
-
D.
\(\{ 0;1;2\} \)
Cho góc \(\alpha \) nhọn. Khẳng định nào sau đây đúng?
-
A.
\(\tan \alpha > 0\)
-
B.
\(\sin \alpha < 0\)
-
C.
\(\cos \alpha < 0\)
-
D.
\(\cot \alpha < 0\)
Cho P: “3x + 6 = 0”.
a) P là một mệnh đề.
b) P là một mệnh đề chứa biến.
c) Với x = -2 thì P là mệnh đề đúng.
d) Với x = 2 thì P là mệnh đề đúng.
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II. Gọi x, y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng.
a) Biểu thức biểu diễn số kg chất A chiết xuất được là 20x + 10y.
b) Biểu thức biểu diễn số kg chất B chiết xuất được là 1,5x + 0,6y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + y \ge 14}\\\begin{array}{l}5x + 2y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\).
d) Phải dùng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II để chi phí nguyên liệu là rẻ nhất.
Cho tam giác ABC biết a = BC = 3 cm, b = AC = 4 cm, \(\widehat C = {30^o}\). Khi đó
a) \(\cos \widehat C = \frac{{\sqrt 3 }}{2}\).
b) \(\cos (\widehat A + \widehat B) = \frac{{\sqrt 3 }}{2}\).
c) \(c \approx 3,05\) cm.
d) \(\cos A \approx 0,68\).
Cho các tập hợp \(A = \{ 0;1;2;3;5;7;11\} \), B = {n | n là số nguyên tố; n < 11}.
a) \(B \subset A\).
b) \(A \cap B = \{ 2;3;5;7\} \).
c) \(A\backslash B = \{ 0;1;11\} \).
d) A = B.
Có bao nhiêu giá trị nguyên của m để mệnh đề chứa biến “\( - {x^2} + 2mx - 4 < 0\)” là mệnh đề đúng?
Đáp án:
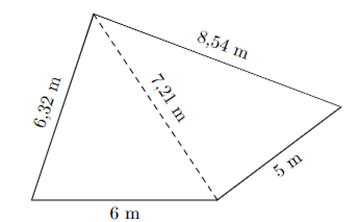
Một mảnh đất có dạng hình tứ giác như hình vẽ. Diện tích (làm tròn đến hàng đơn vị) mảnh đất đó là bao nhiêu?
Đáp án:
Tính \(C = {\sin ^2}{10^o} + {\sin ^2}{20^o} + ... + {\sin ^2}{170^o} + {\sin ^2}{180^o}\).
Đáp án:
Một cửa hàng bán lẻ hai loại hạt cà phê. Loại thứ nhất giá 140 nghìn đồng/kg. Loại thứ hai giá 180 nghìn đồng/kg. Cửa hàng trộn x kg loại thứ nhất và y kg loại thứ hai sao cho hạt cà phê đã trộn có giá không quá 170 nghìn đồng/kg. Bất phương trình bậc nhất hai ẩn x, y thỏa mãn điều kiện bài toán là \(ax + y \le b\). Tính b – 2a.
Đáp án:
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit thức ăn mỗi ngày. Mỗi kg thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua tối đa 1,6 kg thịt bò và 1,1 kg thịt lợn; giá tiền 1 kg thịt bò là 45 nghìn đồng, 1 kg thịt lợn là 35 nghìn đồng. Hỏi gia đình đó phải bỏ ra ít nhất bao nhiêu tiền (đơn vị: nghìn đồng) để đạt các yêu cầu trên?
Đáp án:
Một cuộc khảo sát về khách du lịch thành phố Hà Nội cho thấy trong 1230 khách du lịch được phỏng vấn, có 823 khách du lịch đã đến Hồ Gươm, 567 du khách đến thăm Lăng Bác. Toàn bộ khách phỏng vấn đã đến ít nhất một trong hai địa điểm trên. Hỏi có bao nhiêu khách du lịch vừa đến Hồ Gươm, vừa thăm Lăng Bác?
Đáp án:
Lời giải và đáp án
Câu nào sau đây là một mệnh đề?
-
A.
Số 30 có phải số chẵn không?
-
B.
Số 30 là số chẵn.
-
C.
2x – 1 là số lẻ.
-
D.
\({x^3} + 1 = 0\).
Đáp án : B
Mệnh đề là một câu khẳng định có tính đúng, sai.
“30 là số chẵn” là mệnh đề.
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(x - {y^2} < 0\)
-
B.
\(x + y < 3xy\)
-
C.
\(x + \frac{1}{y} \ge 0\)
-
D.
\(\frac{x}{3} + \frac{y}{2} < 0\)
Đáp án : D
Dựa vào định nghĩa bất phương trình bậc nhất hai ẩn.
Các bất phương trình ở đáp án A, B, C không phải bất phương trình bậc nhất hai ẩn.
Cặp số nào sau đây là một nghiệm của bất phương trình \(x + 2y \le 4\)?
-
A.
\((2;1)\)
-
B.
\((1;2)\)
-
C.
\((1;3)\)
-
D.
\(( - 1;3)\)
Đáp án : A
Thay từng cặp số vào bất phương trình xem cặp số nào thỏa mãn.
Xét \((2;1)\) ta có \(2 + 2.1 \le 4\) (đúng).
Xét \((2;1)\) ta có \(1 + 2.2 \le 4\) (sai).
Xét \((1;3)\) ta có \(1 + 2.3 \le 4\) (sai).
Xét \(( - 1;3)\) ta có \( - 1 + 2.3 \le 4\) (sai).
Vậy cặp số (2;1) là một nghiệm của bất phương trình \(x + 2y \le 4\).
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\) chứa điểm nào trong các điểm sau đây?
-
A.
\((0;0)\)
-
B.
\((1;0)\)
-
C.
\((0; - 2)\)
-
D.
\((0;2)\)
Đáp án : C
Thay lần lượt tọa độ các điểm đã cho vào hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\), nếu thỏa mãn thì điểm đó thuộc miền nghiệm của bất phương trình đã cho.
Với điểm có tọa độ \((0;0)\) ta thấy 2.0 – 5.0 – 1 = -1 không thỏa mãn phương trình \(2x - 5y - 1 > 0\).
Với điểm có tọa độ \((1;0)\) ta thấy 1 + 0 + 1 = 2 không thỏa mãn phương trình \(x + y + 1 < 0\).
Với điểm có tọa độ \((0;2)\) ta thấy 0 + 2 + 1 = 3 không thỏa mãn phương trình \(x + y + 1 < 0\).
Với điểm có tọa độ \((0; - 2)\) ta thấy thỏa mãn mọi phương trình trong hệ.
Vậy miền nghiệm chứa điểm \((0; - 2)\).
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB và \(\widehat A = {60^o}\). Đẳng thức nào sau đây đúng?
-
A.
\({a^2} = {b^2} + {c^2} - 3bc\)
-
B.
\({a^2} = {b^2} + {c^2} + bc\)
-
C.
\({a^2} = {b^2} + {c^2} + 3bc\)
-
D.
\({a^2} = {b^2} + {c^2} - bc\)
Đáp án : D
Dựa vào định lí Cos trong tam giác.
Xét tam giác ABC có ba cạnh a = BC, b = AC, c = AB. Khi đó \({a^2} = {b^2} + {c^2} - 2bc\cos \widehat A\)
\( = {b^2} + {c^2} - 2bc\cos {60^o} = {b^2} + {c^2} - 2bc\frac{1}{2} = {b^2} + {c^2} - bc\).
Cho các tập hợp \(A = \{ 0;2;4;6;8\} \) và \(B = \{ 1;2;3;4;5;6\} \). Tìm \(A\backslash B\).
-
A.
{0;8}
-
B.
{1;3;5}
-
C.
{0;2;8}
-
D.
{2;4;6}
Đáp án : A
\(A\backslash B\) là tập hợp chứa những phần tử thuộc tập hợp A mà không thuộc tập hợp B.
\(A\backslash B = \{ 0;8\} \).
Miền tam giác (kể cả ba cạnh AB, BC, CA) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?

-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \ge 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \le 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \ge 0}\end{array}} \right.\)
Đáp án : A
Thay tọa độ của điểm thuộc miền nghiệm vào các bất phương trình xem có thỏa mãn không.
Dùng phương pháp loại trừ.
Xét đáp án A:
Thay điểm có tọa độ \(\left( {0;\frac{3}{2}} \right)\) vào cả ba bất phương trình của hệ đều thỏa mãn.
Vậy đáp án A đúng.
Xét đáp án B:
Thay điểm có tọa độ \(\left( {0;\frac{3}{2}} \right)\) vào bất phương trình thứ nhất của hệ được \(0 + \frac{3}{2} - 2 \ge 0\) (vô lí).
Vậy bất phương trình ở đáp án B sai.
Xét đáp án C:
Thay điểm có tọa độ \(\left( {0;\frac{3}{2}} \right)\) vào bất phương trình thứ hai của hệ được \(0 - \frac{3}{2} + 2 \le 0\) (vô lí).
Vậy bất phương trình ở đáp án C sai.
Xét đáp án D:
Thay điểm có tọa độ \(\left( {0;\frac{3}{2}} \right)\) vào bất phương trình thứ ba của hệ được \(0 - 2.\frac{3}{2} + 2 \ge 0\) (vô lí).
Vậy bất phương trình ở đáp án D sai.
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({180^o} - \alpha ) = - \sin \alpha \)
-
B.
\(\cos ({180^o} - \alpha ) = \cos \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Đáp án : C
Dựa vào mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau, hai góc bù nhau.
Ta có:
\(\sin ({180^o} - \alpha ) = \sin \alpha \) suy ra A sai.
\(\cos ({180^o} - \alpha ) = - \cos \alpha \) suy ra B sai.
\(\sin ({90^o} - \alpha ) = \cos \alpha \) suy ra C đúng, D sai.
Với \(x \in \mathbb{R}\), tìm mệnh đề đúng trong các mệnh đề sau.
-
A.
\(\forall x \in ( - \infty ;1] \Leftrightarrow x < 1\)
-
B.
\(\forall x \in ( - \infty ;1] \Leftrightarrow x \le 1\)
-
C.
\(\forall x \in ( - \infty ;1) \Leftrightarrow x \le 1\)
-
D.
\(\forall x \in ( - \infty ;1) \Leftrightarrow x < - 1\)
Đáp án : B
Xét tính đúng sai của mệnh đề.
Với \(x \in \mathbb{R}\):
A sai vì \(\forall x \in ( - \infty ;1] \Leftrightarrow x \le 1\). Từ đó suy ra B đúng.
C, D sai vì \(\forall x \in ( - \infty ;1) \Leftrightarrow x < 1\).
Tam giác ABC có AB = 6, AC = 9, \(\widehat A = {60^o}\). Tính diện tích tam giác ABC.
-
A.
\({S_{\Delta ABC}} = \frac{{27\sqrt 3 }}{2}\)
-
B.
\({S_{\Delta ABC}} = \frac{{27}}{2}\)
-
C.
\({S_{\Delta ABC}} = \frac{{27\sqrt 3 }}{4}\)
-
D.
\({S_{\Delta ABC}} = \frac{{27}}{4}\)
Đáp án : A
Áp dụng công thức \({S_{\Delta ABC}} = \frac{1}{2}AB.aC.\sin \widehat A\).
Ta có \({S_{\Delta ABC}} = \frac{1}{2}AB.AC.\sin \widehat A = \frac{1}{2}6.9\sin {60^o} = \frac{{27\sqrt 3 }}{2}\).
Cho tập hợp \(A = \{ 0;2;3;4;5\} \). Tập hợp nào sau đây là tập con của A?
-
A.
\(\{ 1;4\} \)
-
B.
\(\{ 3;8\} \)
-
C.
\(\{ 0;2;5\} \)
-
D.
\(\{ 0;1;2\} \)
Đáp án : C
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B.
Ta có:
\(\{ 1;4\} \not{ \subset }\{ 0;2;3;4;5\} = A\). Loại A.
\(\{ 3;8\} \not{ \subset }\{ 0;2;3;4;5\} = A\). Loại B.
\(\{ 0;2;5\} \subset \{ 0;2;3;4;5\} = A\). Chọn C.
\(\{ 0;1;2\} \not{ \subset }\{ 0;2;3;4;5\} = A\). Loại D.
Cho góc \(\alpha \) nhọn. Khẳng định nào sau đây đúng?
-
A.
\(\tan \alpha > 0\)
-
B.
\(\sin \alpha < 0\)
-
C.
\(\cos \alpha < 0\)
-
D.
\(\cot \alpha < 0\)
Đáp án : A
Dựa vào giá trị lượng giác của góc.
\(\alpha \) là góc nhọn nên \(\sin \alpha > 0\), \(\cos \alpha > 0\), suy ta \(\tan \alpha > 0\), \(\cot \alpha > 0\).
Cho P: “3x + 6 = 0”.
a) P là một mệnh đề.
b) P là một mệnh đề chứa biến.
c) Với x = -2 thì P là mệnh đề đúng.
d) Với x = 2 thì P là mệnh đề đúng.
a) P là một mệnh đề.
b) P là một mệnh đề chứa biến.
c) Với x = -2 thì P là mệnh đề đúng.
d) Với x = 2 thì P là mệnh đề đúng.
a) Mệnh đề là một khẳng định có tính đúng, sai.
b) Mệnh đề chứa biến là khẳng định mang tính đúng, sai phụ thuộc vào biến.
c) Xét tính đúng, sai của mệnh đề.
d) Xét tính đúng, sai của mệnh đề.
a) Sai . P là một khẳng định không mang tính đúng, sai nên không phải mệnh đề.
b) Đúng. P là một mệnh đề chứa biến vì là khẳng định mang tính đúng, sai phụ thuộc vào biến x.
c) Đúng. Với x = -2 thì 3(-2) + 6 = 0 nên P là mệnh đề đúng.
d) Sai. Với x = 2 thì 3.2 + 6 = 12 nên P là mệnh đề sai.
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II. Gọi x, y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng.
a) Biểu thức biểu diễn số kg chất A chiết xuất được là 20x + 10y.
b) Biểu thức biểu diễn số kg chất B chiết xuất được là 1,5x + 0,6y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + y \ge 14}\\\begin{array}{l}5x + 2y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\).
d) Phải dùng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II để chi phí nguyên liệu là rẻ nhất.
a) Biểu thức biểu diễn số kg chất A chiết xuất được là 20x + 10y.
b) Biểu thức biểu diễn số kg chất B chiết xuất được là 1,5x + 0,6y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + y \ge 14}\\\begin{array}{l}5x + 2y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\).
d) Phải dùng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II để chi phí nguyên liệu là rẻ nhất.
Lập hệ bất phương trình.
a) Đúng. Biểu thức biểu diễn số kg chất A chiết xuất được là 20x + 10y.
b) Sai. Biểu thức biểu diễn số kg chất B chiết xuất được là 0,6x + 1,5y.
c) Sai. Với số tấn nguyên liệu loại I là x, số tấn nguyên liệu loại II là y, ta có:
Số kg chất A chiết xuất được là 20x + 10y (kg).
Số kg chất B chiết xuất được là 1,5x + 0,6y (kg).
Theo giả thiết ta có \(\left\{ {\begin{array}{*{20}{c}}{20x + 10y \ge 14}\\\begin{array}{l}0,6x + 1,5y \ge 9\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{c}}{2x + y \ge 14}\\\begin{array}{l}2x + 5y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\).
d) Đúng. Vẽ miền nghiệm của hệ:
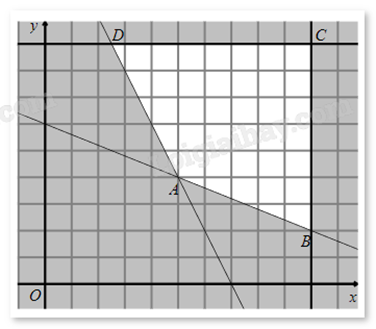
Ta thấy miền nghiệm của hệ là một miền tứ giác ABCD kể cả biên, trong đó A(5;4), B(10;2), C(10;9), \(D\left( {\frac{5}{2};9} \right)\).
Số tiền mua nguyên liệu là P = 4x + 3y.
P đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Thay tọa độ các điểm trên vào P, thấy P đạt giá trị nhỏ nhất bằng 32 tại A(5;4).
Vậy, để chi phí nguyên liệu nhỏ nhất, cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II.
Cho tam giác ABC biết a = BC = 3 cm, b = AC = 4 cm, \(\widehat C = {30^o}\). Khi đó
a) \(\cos \widehat C = \frac{{\sqrt 3 }}{2}\).
b) \(\cos (\widehat A + \widehat B) = \frac{{\sqrt 3 }}{2}\).
c) \(c \approx 3,05\) cm.
d) \(\cos A \approx 0,68\).
a) \(\cos \widehat C = \frac{{\sqrt 3 }}{2}\).
b) \(\cos (\widehat A + \widehat B) = \frac{{\sqrt 3 }}{2}\).
c) \(c \approx 3,05\) cm.
d) \(\cos A \approx 0,68\).
a) Dựa vào giá trị lượng giác của một góc.
b) Sử dụng công thức \(\cos ({180^o} - \alpha ) = - \cos \alpha \).
c) Sử dụng định lý Cosin trong tam giác.
d) Sử dụng định lý Cosin trong tam giác.
a) Đúng. Ta có \(\cos {30^o} = \frac{{\sqrt 3 }}{2}\).
b) Sai. Ta có \[\widehat C = {180^o} - (\widehat A + \widehat B)\] nên \(\cos (\widehat A + \widehat B) = - \cos \widehat C = - \frac{{\sqrt 3 }}{2}\).
c) Sai . Ta có \({c^2} = {b^2} + {a^2} - 2ba\cos C = {4^2} + {3^2} - 2.4.3.\frac{{\sqrt 3 }}{2} = 25 - 12\sqrt 3 \Rightarrow c \approx 2,05\).
d) Đúng. Ta có \(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{4^2} + 25 - 12\sqrt 3 - {3^2}}}{{2.4.\sqrt {25 - 12\sqrt 3 } }} \approx 0,68\).
Cho các tập hợp \(A = \{ 0;1;2;3;5;7;11\} \), B = {n | n là số nguyên tố; n < 11}.
a) \(B \subset A\).
b) \(A \cap B = \{ 2;3;5;7\} \).
c) \(A\backslash B = \{ 0;1;11\} \).
d) A = B.
a) \(B \subset A\).
b) \(A \cap B = \{ 2;3;5;7\} \).
c) \(A\backslash B = \{ 0;1;11\} \).
d) A = B.
a) B là tập hợp con của A nếu mọi phần tử của B đều thuộc A.
b) Giao của hai tập hợp là tập hợp gồm các phần tử thuộc cả hai tập hợp.
c) A\B là tập hợp gồm các phần tử thuộc A mà không thuộc B.
d) Hai tập hợp bằng nhau khi mọi phần tử thuộc tập hợp này đều thuộc tập hợp kia và ngược lại.
Ta có: \(A = \{ 0;1;2;3;5;7;11\} \), \(B = \{ 2;3;5;7\} \).
a) Đúng . Vì \(\{ 2;3;5;7\} \subset A\) nên \(B \subset A\).
b) Đúng. \(A \cap B = \{ 2;3;5;7\} \).
c) Đúng. \(A\backslash B = \{ 0;1;11\} \).
d) Sai . Hai tập hợp A và B không bằng nhau vì A gồm các phần tử không thuộc B.
Có bao nhiêu giá trị nguyên của m để mệnh đề chứa biến “\( - {x^2} + 2mx - 4 < 0\)” là mệnh đề đúng?
Đáp án:
Đáp án:
Tìm số giá trị nguyên của m để \( - {x^2} + 2mx - 4 < 0\).
Để \( - {x^2} + 2mx - 4 < 0\) với mọi x thì \(\left\{ {\begin{array}{*{20}{c}}{\Delta ' < 0}\\{a < 0}\end{array}} \right.\).
Giải bất phương trình \(\Delta ' < 0\) ta được:
\({m^2} - ( - 1).( - 4) < 0\)
\({m^2} - 4 < 0\)
\( - 2 < x < 2\).
Giải bất phương trình a < 0 ta được:
a = -1 < 0 (luôn đúng).
Vậy có 3 giá trị nguyên của m là -1; 0; 1 để mệnh đề đúng.
Một mảnh đất có dạng hình tứ giác như hình vẽ. Diện tích (làm tròn đến hàng đơn vị) mảnh đất đó là bao nhiêu?

Đáp án:
Đáp án:
Sử dụng công thức Heron.
Hình tứ diện được chia làm hai tam giác. Gọi tam giác có kích thước 6,32 m, 7,21 m và 6 m là tam giác 1. Tam giác còn lại là tam giác 2.
Nửa chu vi mỗi tam giác là:
\({p_1} = \frac{{6,32 + 7,21 + 6}}{2} = 9,765\), \({p_2} = \frac{{8,54 + 7,21 + 5}}{2} = 10,375\).
Diện tích tứ giác là \({S_1} + {S_2} = \sqrt {9,765.(9,765 - 6,32).(9,765 - 7,21).(9,765 - 6)} \)
\( + \sqrt {10,375.(10,375 - 8,54).(10,375 - 7,21).(10,375 - 5)} \approx 36\) \({m^2}\).
Tính \(C = {\sin ^2}{10^o} + {\sin ^2}{20^o} + ... + {\sin ^2}{170^o} + {\sin ^2}{180^o}\).
Đáp án:
Đáp án:
Sử dụng công thức \(\sin ({90^o} - \alpha ) = \cos \alpha \), \(\sin ({180^o} - \alpha ) = \sin \alpha \).
Ta có: \(C = {\sin ^2}{10^o} + {\sin ^2}{20^o} + ... + {\sin ^2}{170^o} + {\sin ^2}{180^o}\)
\( = ({\sin ^2}{10^o} + {\sin ^2}{80^o}) + ({\sin ^2}{20^o} + {\sin ^2}{70^o}) + ... + ({\sin ^2}{40^o} + {\sin ^2}{50^o}) + {\sin ^2}{90^o} + ... + {\sin ^2}{180^o}\)
\( = ({\sin ^2}{10^o} + {\cos ^2}{10^o}) + ({\sin ^2}{20^o} + {\cos ^2}{20^o}) + ... + ({\sin ^2}{40^o} + {\cos ^2}{40^o}) + 1 + {\sin ^2}{80^o} + ... + {\sin ^2}{0^o}\)
\( = 1 + 1 + 1 + 1 + 1 + {\sin ^2}{80^o} + {\sin ^2}{70^o} + ... + {\sin ^2}{10^o}\)
\( = 5 + 1 + 1 + 1 + 1 = 9\).
Một cửa hàng bán lẻ hai loại hạt cà phê. Loại thứ nhất giá 140 nghìn đồng/kg. Loại thứ hai giá 180 nghìn đồng/kg. Cửa hàng trộn x kg loại thứ nhất và y kg loại thứ hai sao cho hạt cà phê đã trộn có giá không quá 170 nghìn đồng/kg. Bất phương trình bậc nhất hai ẩn x, y thỏa mãn điều kiện bài toán là \(ax + y \le b\). Tính b – 2a.
Đáp án:
Đáp án:
Lập bất phương trình bậc nhất hai ẩn biểu diễn giá tiền cà phê.
Số tiền cần để mua x kg loại cà phê thứ nhất là 140000x (đồng).
Số tiền cần để mua y kg loại cà phê thứ hai là 180000y (đồng).
Vì giá tiền loại cà phê sau khi trộn không vượt quá 170000 đồng nên ta có bất phương trình
\(140000x + 180000y \le 170000(x + y)\) hay \( - 3 + y \le 0\).
Suy ra a = -3, b = 0.
Vậy b – 2a = 0 – 2.(-3) = 6.
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit thức ăn mỗi ngày. Mỗi kg thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua tối đa 1,6 kg thịt bò và 1,1 kg thịt lợn; giá tiền 1 kg thịt bò là 45 nghìn đồng, 1 kg thịt lợn là 35 nghìn đồng. Hỏi gia đình đó phải bỏ ra ít nhất bao nhiêu tiền (đơn vị: nghìn đồng) để đạt các yêu cầu trên?
Đáp án:
Đáp án:
Lập hệ bất phương trình.
Gọi x, y lần lượt là số kg thịt bò và thịt lợn gia đình đó mua mỗi ngày (\(0 \le x \le 1,6\), \(0 \le y \le 1,1\)).
Số đơn vị protein mỗi ngày là 800x + 600y, số đơn vị lipit mỗi ngày là 200x + 400y.
Vì gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit mỗi ngày nên ta có hệ bất phương trình: \(\left\{ \begin{array}{l}800x + 600y \ge 900\\200x + 400y \ge 400\\0 \le x \le 1,6\\0 \le y \le 1,1\end{array} \right.\) hay \(\left\{ \begin{array}{l}8x + 6y \ge 9\\x + 2y \ge 2\\0 \le x \le 1,6\\0 \le y \le 1,1\end{array} \right.\) (*).
Số tiền cần bỏ ra để mua thịt bò, thịt lợn mỗi ngày là f(x;y) = 45x + 35y (nghìn đồng).
Bài toán trở thành tìm giá trị nhỏ nhất của hàm số f(x;y) trên miền nghiệm của hệ bất phương trình (*).
Miền nghiệm của hệ bất phương trình (*) là tứ giác ABCD (kể cả biên).
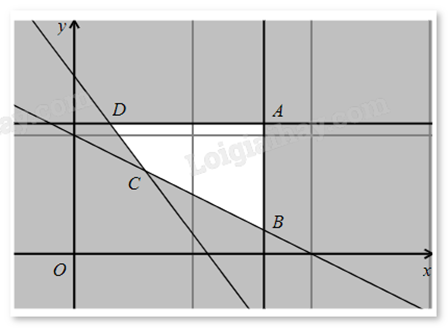
Hàm số f(x;y) sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình (*) khi (x;y) là tọa độ một trong các đỉnh A(1,6;1,1), B(1,6;0,2), C(0,6;0,7), D(0,3;1,1).
Thay tọa độ từng điểm vào f(x;y) thấy hàm số đạt giá trị nhỏ nhất bằng 51,1 khi (x;y) = (0,6;0,7).
Vậy gia đình cần bỏ ra ít nhất 51,1 nghìn đồng để mua thịt bò và thịt lợn mỗi ngày.
Một cuộc khảo sát về khách du lịch thành phố Hà Nội cho thấy trong 1230 khách du lịch được phỏng vấn, có 823 khách du lịch đã đến Hồ Gươm, 567 du khách đến thăm Lăng Bác. Toàn bộ khách phỏng vấn đã đến ít nhất một trong hai địa điểm trên. Hỏi có bao nhiêu khách du lịch vừa đến Hồ Gươm, vừa thăm Lăng Bác?
Đáp án:
Đáp án:
Sử dụng kiến thức về các phép toán trên tập hợp.
Nếu A và B là hai tập hợp hữu hạn thì \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\).
Gọi A là tập hợp các du khách du lịch Hồ Gươm, B là tập hợp các du khách thăm Lăng Bác.
Khi đó, số phần tử của hai tập hợp A, B là \(n(A) = 823\) và \(n(B) = 567\).
Theo đề bài, số du khách đã đến một trong hai địa điểm là \(n(A \cup B) = 1230\).
Số du khách đã đến cả hai địa điểm là \(n(A \cap B)\).
Ta có: \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)
\(1230 = 823 + 567 - n(A \cap B)\)
\(n(A \cap B) = 160\).