Đề thi giữa kì 1 Toán 10 - Đề số 12
Phần trắc nghiệm
Đề bài
Phủ định của mệnh đề “\(\exists x \in \mathbb{R},{x^2} - x + 1 < 0\)” là mệnh đề
-
A.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”
-
B.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 < 0\)”
-
C.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 > 0\)”
-
D.
“\(\exists x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(x + 4{y^3} > 0\)
-
B.
\(x + y = 3\)
-
C.
\(x + \frac{1}{{{y^2}}} \ge 0\)
-
D.
\(x + \frac{y}{2} < 0\)
Bất phương trình \(3x - 2(y - x + 1) > 0\) tương đương với bất phương trình nào sau đây?
-
A.
\(x - 2y - 2 > 0\)
-
B.
\(5x - 2y - 2 > 0\)
-
C.
\(5x - 2y - 1 > 0\)
-
D.
\(4x - 2y - 2 > 0\)
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{3x + y \ge 9}\\{x \ge y - 3}\\{2y \ge 8 - x}\\{y \le 6}\end{array}} \right.\) chứa điểm nào trong các điểm sau đây?
-
A.
O(0;0)
-
B.
M(1;2)
-
C.
N(2;1)
-
D.
P(8;4)
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB. Khi đó
-
A.
\({a^2} = {b^2} + {c^2} + 2bc\cos \widehat {BAC}\)
-
B.
\({a^2} = {b^2} + {c^2} - 2bc\sin \widehat {BAC}\)
-
C.
\({a^2} = {b^2} + {c^2} + 2bc\sin \widehat {BAC}\)
-
D.
\({a^2} = {b^2} + {c^2} - 2bc\cos \widehat {BAC}\)
Cho các tập hợp \(A = \{ x \in \mathbb{R}|x \le - 2\} \) và \(B = \{ x \in \mathbb{R}| - 2 < x \le 8\} \). Tìm \(A \cup B\).
-
A.
[-2;8]
-
B.
(\( - \infty \);8]
-
C.
{-2}
-
D.
\(\emptyset \)
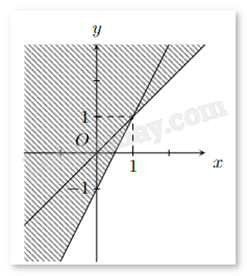
Phần không tô đậm (không kể biên) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?
-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x - y \ge 0}\\{2x - y \ge 1}\end{array}} \right.\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x - y > 0}\\{2x - y > 1}\end{array}} \right.\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x - y < 0}\\{2x - y > 1}\end{array}} \right.\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x - y < 0}\\{2x - y < 1}\end{array}} \right.\)
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({90^o} - \alpha ) = - \cos \alpha \)
-
B.
\(\sin ({90^o} - \alpha ) = - \sin \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Với \(x \in \mathbb{R}\), tìm mệnh đề đúng trong các mệnh đề sau.
-
A.
\(\forall x \in ( - 4;1] \Leftrightarrow - 4 < x < 1\)
-
B.
\(\forall x \in ( - 4;1] \Leftrightarrow - 4 \le x < 1\)
-
C.
\(\forall x \in ( - 4;1] \Leftrightarrow - 4 < x \le 1\)
-
D.
\(\forall x \in ( - 4;1] \Leftrightarrow - 4 \le x \le 1\)
Tam giác ABC có AB = 4, BC = 7, \(\widehat B = {150^o}\). Tính diện tích tam giác ABC.
-
A.
\({S_{\Delta ABC}} = \frac{{7\sqrt 3 }}{2}\)
-
B.
\({S_{\Delta ABC}} = 14\)
-
C.
\({S_{\Delta ABC}} = 7\)
-
D.
\({S_{\Delta ABC}} = 7\sqrt 3 \)
Cho tập hợp \(A = \{ 1;2;3;4\} \). Tập hợp nào sau đây là tập con của A?
-
A.
\(\{ 1;3\} \)
-
B.
\(\{ 2;5\} \)
-
C.
\(\{ 0;3\} \)
-
D.
\(\{ 0;1;2\} \)
Cho góc \(\alpha \) tù. Khẳng định nào sau đây đúng?
-
A.
\(\tan \alpha > 0\)
-
B.
\(\sin \alpha < 0\)
-
C.
\(\cos \alpha > 0\)
-
D.
\(\cot \alpha < 0\)
Cho hai mệnh đề sau:
P: “Hình bình hành có một góc vuông là hình chữ nhật”.
Q: “Số 7 là hợp số”.
a) Mệnh đề P là mệnh đề đúng.
b) Mệnh đề Q là mệnh đề đúng.
c) Mệnh đề \(P \Rightarrow Q\) là mệnh đề đúng.
d) Mệnh đề \(Q \Rightarrow P\) là mệnh đề đúng.
Trong một cuộc thi gói bánh vào dịp năm mới, mỗi đội chơi được sử dụng tối đa 20 kg gạo nếp, 2 kg thịt ba chỉ, 5 kg đậu xanh để gói bánh chưng và bánh tét. Để gói một cái bánh chưng cần 0,4 kg gạo nếp, 0,05 kg thịt và 0,1 kg đậu xanh. Để gói một cái bánh tét cần 0,6 kg gạo nếp, 0,075 kg thịt và 0,15 kg đậu xanh. Gọi số bánh chưng gói được là x, số bánh tét gói được là y.
a) Biểu thức biểu diễn số kg gạo nếp cần dùng là 0,4x + 0,6y.
b) Biểu thức biểu diễn số thịt ba chỉ cần dùng là 0,05x + 0,1y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + 3y \le 80}\\{x,y \ge 0}\end{array}} \right.\).
d) Mỗi cái bánh chưng nhận được 5 điểm thưởng, mỗi cái bánh tét nhận được 7 điểm thưởng. Để điểm thưởng lớn nhất thì gói 35 cái bánh chưng và 5 cái bánh tét.
Cho tam giác ABC có AC = b = 7, AB = c = 5, \(\cos A = \frac{3}{5}\).
a) Góc A là góc tù.
b) \(\sin A = - \frac{4}{5}\).
c) \(a = 4\sqrt 2 \).
d) Độ dài đường cao hạ từ đỉnh A bằng \(\frac{{7\sqrt 2 }}{2}\).
Cho các tập hợp \(A = \{ n \in \mathbb{N}|3 < {n^2} < 10\} \), \(B = \{ x \in \mathbb{R}|2x - {x^2} = 0\} \).
a) \(4 \in A\).
b) Tập hợp B chỉ có 1 phần tử.
c) Tập hợp A có 4 tập hợp con.
d) Tập hợp \(A \cap B\) có duy nhất 1 phần tử.
Xét mệnh đề chứa biến P(x): “\(x \in \mathbb{N},{x^2} - 2x = 0\)”. Có bao nhiêu giá trị của biến để được mệnh đề đúng?
Đáp án:
Khoảng cách từ B đến cọc tiêu C không thể đo trực tiếp vì phải qua một đầm lầy. Người ta xác định một điêm A có khoảng cách AB = 5 m và đo được \(\widehat {BAC} = {60^o}\) (xem hình vẽ). Tính khoảng cách BC biết rằng AC = 8 m.
Đáp án:
Cho góc \(\alpha \) (\({0^o} < \alpha < {180^o}\)) thỏa mãn \(\tan \alpha = - \frac{5}{{12}}\). Tính giá trị của biểu thức \(T = \frac{{3\sin \alpha - 5\cos \alpha }}{{4\sin \alpha + \cos \alpha }}\) (làm tròn kết quả đến hàng phần trăm).
Đáp án:
Bạn An cần mua một số tập vẽ và bút chì. Mỗi tập vé giá 10 nghìn đồng, mỗi bút chì giá 5 nghìn đồng. Gọi x, y lần lượt là số tập vẽ và bút chì bạn An có thể mua được \((x,y \in \mathbb{N})\). Nếu bạn An chỉ có 50 nghìn đồng thì x và y thỏa mãn điều kiện \(ax + by \le c\), với a, b, c là các số tự nhiên không lớn hơn 15. Tìm a + b + c.
Đáp án:
Một phân xưởng có hai máy đặc chủng \({M_1}\), \({M_2}\) sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy \({M_1}\) trong 3 giờ và máy \({M_2}\) trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy
\({M_1}\) trong 1 giờ và máy \({M_2}\) trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy \({M_1}\) làm việc không quá 6 giờ một ngày, máy \({M_2}\) làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu (đơn vị: triệu đồng)?
Đáp án:
Trong số 35 học sinh của lớp 10A, có 20 học sinh thích môn bóng đá, 14 học sinh thích môn bóng chuyền và 11 học sinh thích cả hai môn này. Hỏi lớp 10A có bao nhiêu học sinh không thích cả hai môn này?
Đáp án:
Lời giải và đáp án
Phủ định của mệnh đề “\(\exists x \in \mathbb{R},{x^2} - x + 1 < 0\)” là mệnh đề
-
A.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”
-
B.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 < 0\)”
-
C.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 > 0\)”
-
D.
“\(\exists x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”
Đáp án : A
Phủ định của “\(\forall \)” là “\(\exists \)”.
Phủ định của “\( < \)” là “\( \ge \)”.
Mệnh đề phủ định của mệnh đề trên là “\(\forall x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”.
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(x + 4{y^3} > 0\)
-
B.
\(x + y = 3\)
-
C.
\(x + \frac{1}{{{y^2}}} \ge 0\)
-
D.
\(x + \frac{y}{2} < 0\)
Đáp án : D
Dựa vào định nghĩa bất phương trình bậc nhất hai ẩn.
Các phương trình, bất phương trình ở đáp án A, B, C không phải bất phương trình bậc nhất hai ẩn.
Bất phương trình \(3x - 2(y - x + 1) > 0\) tương đương với bất phương trình nào sau đây?
-
A.
\(x - 2y - 2 > 0\)
-
B.
\(5x - 2y - 2 > 0\)
-
C.
\(5x - 2y - 1 > 0\)
-
D.
\(4x - 2y - 2 > 0\)
Đáp án : B
Rút gọn vế trái của bất phương trình.
\(3x - 2(y - x + 1) > 0\)
\(3x - 2y + 2x - 2 > 0\)
\(5x - 2y - 2 > 0\).
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{3x + y \ge 9}\\{x \ge y - 3}\\{2y \ge 8 - x}\\{y \le 6}\end{array}} \right.\) chứa điểm nào trong các điểm sau đây?
-
A.
O(0;0)
-
B.
M(1;2)
-
C.
N(2;1)
-
D.
P(8;4)
Đáp án : D
Thay lần lượt tọa độ các điểm đã cho vào hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{3x + y \ge 9}\\{x \ge y - 3}\\{2y \ge 8 - x}\\{y \le 6}\end{array}} \right.\), nếu thỏa mãn thì điểm đó thuộc miền nghiệm của bất phương trình đã cho.
Với điểm có tọa độ (0;0) ta thấy 3.0 + 0 = 0 không thỏa mãn phương trình \(3x + y \ge 9\).
Với điểm có tọa độ (1;2) ta thấy 3.1 + 2 = 5 không thỏa mãn phương trình \(3x + y \ge 9\).
Với điểm có tọa độ (2;1) ta thấy 3.2 + 1 = 6 không thỏa mãn phương trình
\(3x + y \ge 9\).
Với điểm có tọa độ (8;4) ta thấy thỏa mãn mọi phương trình trong hệ.
Vậy miền nghiệm chứa điểm P(8;4).
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB. Khi đó
-
A.
\({a^2} = {b^2} + {c^2} + 2bc\cos \widehat {BAC}\)
-
B.
\({a^2} = {b^2} + {c^2} - 2bc\sin \widehat {BAC}\)
-
C.
\({a^2} = {b^2} + {c^2} + 2bc\sin \widehat {BAC}\)
-
D.
\({a^2} = {b^2} + {c^2} - 2bc\cos \widehat {BAC}\)
Đáp án : D
Dựa vào định lí Cos trong tam giác.
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB. Khi đó \({a^2} = {b^2} + {c^2} - 2bc\cos \widehat {BAC}\).
Cho các tập hợp \(A = \{ x \in \mathbb{R}|x \le - 2\} \) và \(B = \{ x \in \mathbb{R}| - 2 < x \le 8\} \). Tìm \(A \cup B\).
-
A.
[-2;8]
-
B.
(\( - \infty \);8]
-
C.
{-2}
-
D.
\(\emptyset \)
Đáp án : B
Hợp của hai tập hợp A và B là tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B.
\(A \cup B = ( - \infty ;8]\).
Phần không tô đậm (không kể biên) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?

-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x - y \ge 0}\\{2x - y \ge 1}\end{array}} \right.\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x - y > 0}\\{2x - y > 1}\end{array}} \right.\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x - y < 0}\\{2x - y > 1}\end{array}} \right.\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x - y < 0}\\{2x - y < 1}\end{array}} \right.\)
Đáp án : B
Xét miền nghiệm có chứa biên hay không.
Thay tọa độ của điểm bất kì vào hệ bất phương trình xem có thỏa mãn không.
Dùng phương pháp loại trừ.
Do miền nghiệm không chứa biên nên ta loại đáp án A.
Lấy điểm M(0;1) không thuộc miền nghiệm của cả hai bất phương trình trong hệ bất phương trình, thay tọa độ điểm M vào đáp án B, C, D, nếu không thỏa mãn cả hai bất phương trình trong hệ thì đáp án đúng.
Xét đáp án B, ta thấy \(\left\{ {\begin{array}{*{20}{c}}{0 - 1 = - 1 > 0}\\{2.0 - 1 = 1 > 1}\end{array}} \right.\) không thỏa mãn cả hai bất phương trình. Chọn B.
Xét đáp án C, ta thấy \(\left\{ {\begin{array}{*{20}{c}}{0 - 1 = - 1 < 0}\\{2.0 - 1 = 1 > 1}\end{array}} \right.\) thỏa mãn một bất phương trình. Loại C.
Xét đáp án D, ta thấy \(\left\{ {\begin{array}{*{20}{c}}{0 - 1 = - 1 < 0}\\{2.0 - 1 = 1 < 1}\end{array}} \right.\) thỏa mãn một bất phương trình. Loại D.
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({90^o} - \alpha ) = - \cos \alpha \)
-
B.
\(\sin ({90^o} - \alpha ) = - \sin \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Đáp án : C
Dựa vào mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau.
Với hai góc phụ nhau \(\alpha \) và \({90^o} - \alpha \), ta có \(\sin ({90^o} - \alpha ) = \cos \alpha \).
Với \(x \in \mathbb{R}\), tìm mệnh đề đúng trong các mệnh đề sau.
-
A.
\(\forall x \in ( - 4;1] \Leftrightarrow - 4 < x < 1\)
-
B.
\(\forall x \in ( - 4;1] \Leftrightarrow - 4 \le x < 1\)
-
C.
\(\forall x \in ( - 4;1] \Leftrightarrow - 4 < x \le 1\)
-
D.
\(\forall x \in ( - 4;1] \Leftrightarrow - 4 \le x \le 1\)
Đáp án : C
\(\forall x \in (a;b] \Leftrightarrow a < x \le b\).
Với \(x \in \mathbb{R}\) thì \(\forall x \in [ - 3;2) \Leftrightarrow - 3 \le x < 2\).
Tam giác ABC có AB = 4, BC = 7, \(\widehat B = {150^o}\). Tính diện tích tam giác ABC.
-
A.
\({S_{\Delta ABC}} = \frac{{7\sqrt 3 }}{2}\)
-
B.
\({S_{\Delta ABC}} = 14\)
-
C.
\({S_{\Delta ABC}} = 7\)
-
D.
\({S_{\Delta ABC}} = 7\sqrt 3 \)
Đáp án : C
Áp dụng công thức \({S_{\Delta ABC}} = \frac{1}{2}AB.BC.\sin \widehat B\).
Ta có \({S_{\Delta ABC}} = \frac{1}{2}AB.BC.\sin \widehat B = \frac{1}{2}4.7\sin {150^o} = 7\).
Cho tập hợp \(A = \{ 1;2;3;4\} \). Tập hợp nào sau đây là tập con của A?
-
A.
\(\{ 1;3\} \)
-
B.
\(\{ 2;5\} \)
-
C.
\(\{ 0;3\} \)
-
D.
\(\{ 0;1;2\} \)
Đáp án : A
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B.
Ta có:
\(\{ 1;3\} \subset \{ 1;2;3;4\} = A\). Chọn A.
\(\{ 2;5\} \not{ \subset }\{ 1;2;3;4\} = A\). Loại B.
\(\{ 0;3\} \not{ \subset }\{ 1;2;3;4\} = A\). Loại C.
\(\{ 0;1;2\} \not{ \subset }\{ 1;2;3;4\} = A\). Loại D.
Cho góc \(\alpha \) tù. Khẳng định nào sau đây đúng?
-
A.
\(\tan \alpha > 0\)
-
B.
\(\sin \alpha < 0\)
-
C.
\(\cos \alpha > 0\)
-
D.
\(\cot \alpha < 0\)
Đáp án : D
Dựa vào giá trị lượng giác của góc.
\(\alpha \) là góc tù nên \(\sin \alpha > 0\), \(\cos \alpha < 0\), suy ta \(\tan \alpha < 0\), \(\cot \alpha < 0\).
Cho hai mệnh đề sau:
P: “Hình bình hành có một góc vuông là hình chữ nhật”.
Q: “Số 7 là hợp số”.
a) Mệnh đề P là mệnh đề đúng.
b) Mệnh đề Q là mệnh đề đúng.
c) Mệnh đề \(P \Rightarrow Q\) là mệnh đề đúng.
d) Mệnh đề \(Q \Rightarrow P\) là mệnh đề đúng.
a) Mệnh đề P là mệnh đề đúng.
b) Mệnh đề Q là mệnh đề đúng.
c) Mệnh đề \(P \Rightarrow Q\) là mệnh đề đúng.
d) Mệnh đề \(Q \Rightarrow P\) là mệnh đề đúng.
a, b) Xét tính đúng, sai của mệnh đề.
c, d) Mệnh đề kéo theo \(A \Rightarrow B\) chỉ sai khi A đúng và B sai.
a) Đúng . “Hình bình hành có một góc vuông là hình chữ nhật” là mệnh đề đúng dựa vào dấu hiệu nhận biết hình chữ nhật.
b) Sai. “Số 7 là hợp số” là mệnh đề sai vì số 7 là số nguyên tố.
c) Sai. Vì P đúng, Q sai nên \(P \Rightarrow Q\) là mệnh đề sai.
d) Đúng. Vì P đúng, Q sai nên \(Q \Rightarrow P\) là mệnh đề đúng.
Trong một cuộc thi gói bánh vào dịp năm mới, mỗi đội chơi được sử dụng tối đa 20 kg gạo nếp, 2 kg thịt ba chỉ, 5 kg đậu xanh để gói bánh chưng và bánh tét. Để gói một cái bánh chưng cần 0,4 kg gạo nếp, 0,05 kg thịt và 0,1 kg đậu xanh. Để gói một cái bánh tét cần 0,6 kg gạo nếp, 0,075 kg thịt và 0,15 kg đậu xanh. Gọi số bánh chưng gói được là x, số bánh tét gói được là y.
a) Biểu thức biểu diễn số kg gạo nếp cần dùng là 0,4x + 0,6y.
b) Biểu thức biểu diễn số thịt ba chỉ cần dùng là 0,05x + 0,1y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + 3y \le 80}\\{x,y \ge 0}\end{array}} \right.\).
d) Mỗi cái bánh chưng nhận được 5 điểm thưởng, mỗi cái bánh tét nhận được 7 điểm thưởng. Để điểm thưởng lớn nhất thì gói 35 cái bánh chưng và 5 cái bánh tét.
a) Biểu thức biểu diễn số kg gạo nếp cần dùng là 0,4x + 0,6y.
b) Biểu thức biểu diễn số thịt ba chỉ cần dùng là 0,05x + 0,1y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + 3y \le 80}\\{x,y \ge 0}\end{array}} \right.\).
d) Mỗi cái bánh chưng nhận được 5 điểm thưởng, mỗi cái bánh tét nhận được 7 điểm thưởng. Để điểm thưởng lớn nhất thì gói 35 cái bánh chưng và 5 cái bánh tét.
Lập hệ bất phương trình.
a) Đúng. Biểu thức biểu diễn số kg gạo nếp cần dùng là 0,4x + 0,6y.
b) Sai. Biểu thức biểu diễn số thịt ba chỉ cần dùng là 0,05x + 0,075y.
c) Đúng. Với số bánh chưng gói được là x, số bánh tét gói được là y, ta có:
Số kg gạo nếp cần dùng là 0,4x + 0,6y.
Số thịt ba chỉ cần dùng là 0,05x + 0,075y.
Số đậu xanh cần dùng là 0,1x + 0,15y.
Theo giả thiết ta có \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{0,4x + 0,6y \le 20}\\{0,05x + 0,075y \le 2}\\{0,1x + 0,15y \le 5}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{2x + 3y \le 100}\\{2x + 3y \le 80}\\{2x + 34y \le 100}\end{array}} \right.\), rút gọn ta được \(\left\{ {\begin{array}{*{20}{c}}{x,y \ge 0}\\{2x + 3y \le 80}\end{array}} \right.\).
d) Sai. Vẽ miền nghiệm của hệ:
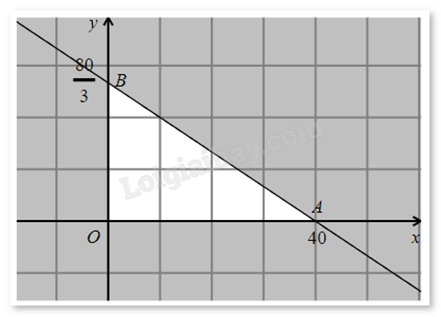
Ta thấy miền nghiệm của hệ là một miền tam giác OAB kể cả biên, trong đó O(0;0), A(40;0), \(B\left( {0;\frac{{80}}{3}} \right)\).
Số điểm thưởng nhận được là P = 5x + 7y.
P đạt giá trị lớn nhất tại một trong các đỉnh của tam giác. Thay tọa độ các điểm trên vào P, thấy P đạt giá trị lớn nhất bằng 200 tại A(40;0).
Vậy, cần gói 40 cái bánh chưng để điểm thưởng lớn nhất.
Cho tam giác ABC có AC = b = 7, AB = c = 5, \(\cos A = \frac{3}{5}\).
a) Góc A là góc tù.
b) \(\sin A = - \frac{4}{5}\).
c) \(a = 4\sqrt 2 \).
d) Độ dài đường cao hạ từ đỉnh A bằng \(\frac{{7\sqrt 2 }}{2}\).
a) Góc A là góc tù.
b) \(\sin A = - \frac{4}{5}\).
c) \(a = 4\sqrt 2 \).
d) Độ dài đường cao hạ từ đỉnh A bằng \(\frac{{7\sqrt 2 }}{2}\).
a) Dựa vào giá trị lượng giác của một góc.
b) Sử dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
c) Sử dụng định lý Cosin trong tam giác.
d) Sử dụng công thức tính diện tích \(S = \frac{1}{2}bc\sin A = \frac{1}{2}{h_a}.a\).
a) Sai. Vì \(\cos A = \frac{3}{5} > 0\) và \({0^o} < A < {180^o}\) nên \(\widehat A\) là góc nhọn.
b) Sai. Ta có \({\sin ^2}A = 1 - {\cos ^2}A = 1 - {\left( {\frac{3}{5}} \right)^2} = \frac{{16}}{{25}}\), khi đó \(\sin A = \pm \frac{4}{5}\).
Vì \(\widehat A\) là góc nhọn nên \(\sin A > 0\), suy ra \(\sin A = \frac{4}{5}\).
c) Đúng . Ta có \({a^2} = {b^2} + {c^2} - 2bc\cos A = {5^2} + {7^2} - 2.5.7.\frac{3}{5} = 32\), suy ra \(a = 4\sqrt 2 \).
d) Đúng. Gọi \({h_a}\) là đường cao ứng với cạnh a trong tam giác.
\(S = \frac{1}{2}bc\sin A = \frac{1}{2}.5.7.\frac{4}{5} = 14\).
Mà \(S = \frac{1}{2}{h_a}.a\) suy ra \({h_a} = \frac{{2S}}{a} = \frac{{2.14}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}\).
Cho các tập hợp \(A = \{ n \in \mathbb{N}|3 < {n^2} < 10\} \), \(B = \{ x \in \mathbb{R}|2x - {x^2} = 0\} \).
a) \(4 \in A\).
b) Tập hợp B chỉ có 1 phần tử.
c) Tập hợp A có 4 tập hợp con.
d) Tập hợp \(A \cap B\) có duy nhất 1 phần tử.
a) \(4 \in A\).
b) Tập hợp B chỉ có 1 phần tử.
c) Tập hợp A có 4 tập hợp con.
d) Tập hợp \(A \cap B\) có duy nhất 1 phần tử.
a) Tìm các phần tử có trong tập hợp A.
b) Tìm các phần tử có trong tập hợp B.
c) Số tập hợp con của tập hợp có n phần tử là .
d) Giao của hai tập hợp là tập hợp gồm các phần tử thuộc cả hai tập hợp.
Ta có: \(A = \{ 2;3\} \), \(B = \{ 0;2\} \).
a) Sai . \(4\not{ \in }A\).
b) Sai. Tập hợp B có 2 phần tử.
c) Đúng. Số tập hợp con của tập hợp A là \({2^2} = 4\), gồm \(\emptyset ,\{ 0\} ,\{ 2\} ,\{ 0;2\} \).
d) Đúng . \(A \cap B = \{ 2\} \).
Xét mệnh đề chứa biến P(x): “\(x \in \mathbb{N},{x^2} - 2x = 0\)”. Có bao nhiêu giá trị của biến để được mệnh đề đúng?
Đáp án:
Đáp án:
Mệnh đề đúng khi giá trị của x là nghiệm của phương trình \({x^2} - 2x = 0\) và \(x \in \mathbb{N}\).
Giải phương trình \({x^2} - 2x = 0\), ta được x = 0 hoặc x = 2.
Mà \(x \in \mathbb{N}\) nên cả hai nghiệm trên đều thỏa mãn.
Vậy có 2 giá trị của biến x để mệnh đề P(x) là mệnh đề đúng.
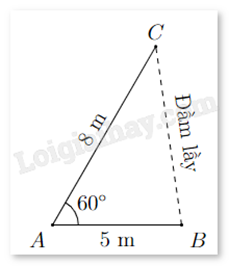
Khoảng cách từ B đến cọc tiêu C không thể đo trực tiếp vì phải qua một đầm lầy. Người ta xác định một điêm A có khoảng cách AB = 5 m và đo được \(\widehat {BAC} = {60^o}\) (xem hình vẽ). Tính khoảng cách BC biết rằng AC = 8 m.

Đáp án:
Đáp án:
Sử dụng định lí Cosin trong tam giác.
Áp dụng định lí Cosin trong tam giác ABC có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
\(B{C^2} = {8^2} + {5^2} - 2.5.8\cos {60^o} = 49\).
Vậy BC = 7 m.
Cho góc \(\alpha \) (\({0^o} < \alpha < {180^o}\)) thỏa mãn \(\tan \alpha = - \frac{5}{{12}}\). Tính giá trị của biểu thức \(T = \frac{{3\sin \alpha - 5\cos \alpha }}{{4\sin \alpha + \cos \alpha }}\) (làm tròn kết quả đến hàng phần trăm).
Đáp án:
Đáp án:
Sử dụng các công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\), \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\).
Vì \({0^o} < \alpha < {180^o}\) nên \(\sin \alpha > 0\).
Lại có \(\tan \alpha = - \frac{5}{{12}} < 0\) nên \(\cos \alpha < 0\).
Ta có \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\)
\(1 + {\left( { - \frac{5}{{12}}} \right)^2} = \frac{1}{{{{\cos }^2}\alpha }}\)
\({\cos ^2}\alpha = \frac{{144}}{{169}}\).
Kết hợp điều kiện suy ra \(\cos \alpha = - \frac{{12}}{{13}}\).
Ta có \({\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - {\left( { - \frac{{12}}{{13}}} \right)^2} = \frac{{25}}{{169}}\).
Kết hợp điều kiện suy ra \(\sin \alpha = \frac{5}{{13}}\).
Ta có \(T = \frac{{3\sin \alpha - 5\cos \alpha }}{{4\sin \alpha + \cos \alpha }} = \frac{{3\frac{5}{{13}} - 5\left( { - \frac{{12}}{{13}}} \right)}}{{4\frac{5}{{13}} + \left( { - \frac{{12}}{{13}}} \right)}} = \frac{{75}}{8} \approx 9,38\).
Bạn An cần mua một số tập vẽ và bút chì. Mỗi tập vé giá 10 nghìn đồng, mỗi bút chì giá 5 nghìn đồng. Gọi x, y lần lượt là số tập vẽ và bút chì bạn An có thể mua được \((x,y \in \mathbb{N})\). Nếu bạn An chỉ có 50 nghìn đồng thì x và y thỏa mãn điều kiện \(ax + by \le c\), với a, b, c là các số tự nhiên không lớn hơn 15. Tìm a + b + c.
Đáp án:
Đáp án:
Lập bất phương trình bậc nhất hai ẩn biểu diễn giá tiền mua tập vẽ và bút chì.
Số tiền bạn An cần để mua tập vẽ là 10000x (đồng).
Số tiền bạn An cần để mua bút chì là 5000y (đồng).
Vì bạn An chỉ có 50000 đồng nên số tiền mua tập vẽ và bút không vượt quá 50000 đồng.
Ta có bất phương trình \(10000x + 5000y \le 50000\) hay \(2x + y \le 10\).
Vì a, b, c là các số tự nhiên không lớn hơn 15 nên ta có a = 2, b = 1 và c = 10.
Vậy a + b + c = 2 + 1 + 10 = 13.
Một phân xưởng có hai máy đặc chủng \({M_1}\), \({M_2}\) sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy \({M_1}\) trong 3 giờ và máy \({M_2}\) trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy
\({M_1}\) trong 1 giờ và máy \({M_2}\) trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy \({M_1}\) làm việc không quá 6 giờ một ngày, máy \({M_2}\) làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu (đơn vị: triệu đồng)?
Đáp án:
Đáp án:
Lập hệ bất phương trình.
Gọi x, y lần lượt là số tấn sản phẩm loại A, B mà phân xưởng này sản xuất trong một ngày (\(x,y \ge 0\)).
Số giờ làm việc trong ngày của máy \({M_1}\) là 3x + y (giờ), số giờ làm việc trong ngày của máy \({M_1}\) là x + y (giờ).
Vì mỗi ngày, máy \({M_1}\) làm việc không quá 6 giờ và máy \({M_2}\) làm việc không quá 4 giờ nên ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{3x + y \le 6}\\{x + y \le 4}\\{x,y \ge 0}\end{array}} \right.\) (*).
Số tiền lãi một ngày của phân xưởng này là f(x;y) = 2x + 2,6y (triệu đồng).
Bài toán trở thành tìm giá trị lớn nhất của hàm số f(x;y) trên miền nghiệm của hệ bất phương trình (*).
Miền nghiệm của hệ bất phương trình (*) là tứ giác OABC (kể cả biên).
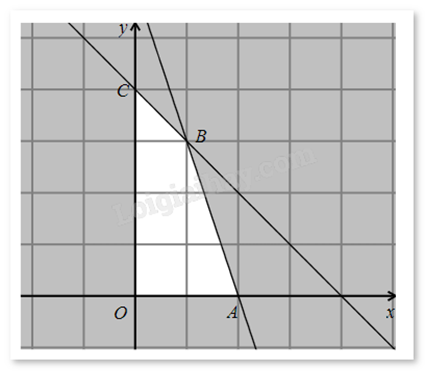
Hàm số f(x;y) sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình (*) khi (x;y) là tọa độ một trong các đỉnh O(0;0), A(2;0), B(1;3), C(0;4).
Thay tọa độ từng điểm vào f(x;y) thấy hàm số đạt giá trị lớn nhất bằng 6,8 khi (x;y) = (1;3).
Vậy số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là 6,8 triệu đồng.
Trong số 35 học sinh của lớp 10A, có 20 học sinh thích môn bóng đá, 14 học sinh thích môn bóng chuyền và 11 học sinh thích cả hai môn này. Hỏi lớp 10A có bao nhiêu học sinh không thích cả hai môn này?
Đáp án:
Đáp án:
Sử dụng kiến thức về các phép toán trên tập hợp.
Nếu A và B là hai tập hợp hữu hạn thì \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\).
Gọi A là tập hợp các học sinh thích môn bóng đá, B là tập hợp các học sinh thích môn bóng chuyển.
Khi đó, số phần tử của hai tập hợp A, B là \(n(A) = 20\) và \(n(B) = 14\).
Theo đề bài, số học sinh thích cả hai môn là \(n(A \cap B) = 11\).
Số học sinh thích ít nhất một môn là \(n(A \cup B)\).
Ta có: \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)
\( = 20 + 14 - 11 = 23\).
Số học sinh không thích cả hai môn là 35 – 23 = 12 (học sinh).