Trắc nghiệm Bài 1: Định lí Thalès trong tam giác Toán 8 Cánh diều
Đề bài
Cho \(AB = 6\,{\rm{cm, }}AC = 18\,{\rm{cm}}\) , tỉ số hai đoạn thẳng \(AB\) và \(AC\) là:
-
A.
\(\frac{1}{2}\)
-
B.
\(\frac{1}{3}\)
-
C.
2
-
D.
3
-
A.
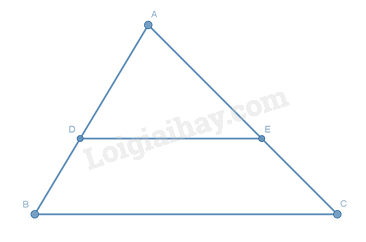
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow DE // BC\)
-
B.
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}} \Rightarrow DE // BC\)
-
C.
\(\frac{{AB}}{{BD}} = \frac{{AC}}{{EC}} \Rightarrow DE // BC\)
-
D.
\(\frac{{AD}}{{DE}} = \frac{{AE}}{{ED}} \Rightarrow DE // BC\)
Cho các đoạn thẳng \(AB = 6\,{\rm{cm,}}\,CD = 4\,{\rm{cm,}}\,PQ = 8\,{\rm{cm,}}\,EF = 10\,{\rm{cm,}}\) \(MN = 25{\rm{ mm, }}RS = 15\,{\rm{mm}}\) . Hãy chọn các phát biểu đúng trong các phát biểu sau:
-
A.
Hai đoạn thẳng \(AB\) và \(PQ\) tỉ lệ với hai đoạn thẳng \(EF\) và \(RS\) .
-
B.
Hai đoạn thẳng \(AB\) và \(RS\) tỉ lệ với hai đoạn thẳng \(EF\) và \(MN\) .
-
C.
Hai đoạn thẳng \(AB\) và \(CD\) tỉ lệ với hai đoạn thẳng \(PQ\) và \(EF\) .
-
D.
Cả 3 phát biểu đều sai.
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Cho điểm \(C\) thuộc đoạn thẳng \(AB\) thỏa mãn \(\frac{{AC}}{{BC}} = \frac{3}{5}\) . Tính tỉ số \(\frac{{AC}}{{AB}}\) .
-
A.
\(\frac{1}{4}\)
-
B.
\(\frac{2}{5}\)
-
C.
\(\frac{3}{8}\)
-
D.
\(\frac{5}{8}\)
Cho các đoạn thẳng \(AB = 8{\rm{ cm, }}CD = 6{\rm{ cm, }}MN = 12{\rm{ cm, }}PQ = x{\rm{ cm}}\) . Tìm \(x\) để \(AB\) và \(CD\) tỉ lệ với \(MN\) và \(PQ\) .
-
A.
7 cm
-
B.
8 cm
-
C.
9 cm
-
D.
10 cm
-
A.
12
-
B.
21
-
C.
14
-
D.
15
-
A.
\(OM = 2,8\)
-
B.
\(OM = 1,8\)
-
C.
\(OM = 3,8\)
-
D.
\(OM = 0,8\)
Cho tam giác \(ABC\) có \(AB = 12{\rm{ cm}}\) , điểm \(D\) thuộc cạnh \(AB\) sao cho \(AD = 8{\rm{ cm}}\) . Kẻ \(DE\) song song với \(BC\,\left( {E \in AC} \right)\) , kẻ \(EF\) song song với \(CD\,\left( {F \in AB} \right)\) . Tính độ dài \(AF\) .
-
A.
2 cm
-
B.
\(\frac{4}{3}\) cm
-
C.
3 cm
-
D.
\(\frac{{16}}{3}\) cm
Cho tứ giác \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Đường thẳng qua \(A\) và song song với \(BC\) cắt \(BD\) ở \(E\) . Đường thẳng qua \(B\) song song với \(AD\) cắt \(AC\) ở \(F\) . Chọn kết luận sai?
-
A.
\(\frac{{OE}}{{OB}} = \frac{{OA}}{{OC}}\)
-
B.
\(\frac{{EF}}{{AB}} = \frac{{OE}}{{OB}}\)
-
C.
\(\frac{{OB}}{{OD}} = \frac{{OF}}{{OA}}\)
-
D.
\(\frac{{OE}}{{OD}} = \frac{{OF}}{{OC}}\)
Cho tứ giác \(ABCD\) . Lấy điểm \(E\) bất kì thuộc \(BD\) . Qua \(E\) kẻ \(EF\) song song với \(AD\left( {F \in AB} \right)\) , kẻ \(EG\) song song với \(DC\,\left( {G \in BC} \right)\) . Chọn khẳng định sai:
-
A.
\(\frac{{BE}}{{ED}} = \frac{{BF}}{{FA}}\)
-
B.
\(FG // AC\)
-
C.
\(\frac{{BF}}{{FA}} = \frac{{BG}}{{GC}}\)
-
D.
\(FG // AD\)
Cho điểm \(M\) thuộc đoạn thẳng \(AB\) sao cho \(MA = 2MB\) . Vẽ về một phía của \(AB\) các tam giác đều \(AMC\) và \(MBD\) . Gọi \(E\) là giao điểm của \(AD\) và \(MC\) , \(F\) là giao điểm của \(BC\) và \(DM\) . Đặt \(MB = a\) . Tính \(ME,MF\) theo \(a\) .
-
A.
\(ME = \frac{a}{2};MF = \frac{a}{3}\)
-
B.
\(ME = MF = \frac{{2a}}{3}\)
-
C.
\(ME = \frac{{2a}}{3};MF = \frac{a}{3}\)
-
D.
\(ME = MF = \frac{a}{3}\)
Cho hình thang \(ABCD\left( {AB // CD} \right)\) có diện tích \(48\,{\rm{c}}{{\rm{m}}^2}\) , \(AB = 4\,{\rm{cm,}}\,CD = 8{\rm{cm}}\) . Gọi \(O\) là giao điểm của hai đường chéo. Tính diện tích tam giác \(COD\)
-
A.
\(\frac{{64}}{3}{\rm{c}}{{\rm{m}}^2}\)
-
B.
\({\rm{15c}}{{\rm{m}}^2}\)
-
C.
\({\rm{16c}}{{\rm{m}}^2}\)
-
D.
\({\rm{32c}}{{\rm{m}}^2}\)
Cho hình thang \(ABCD\,\left( {AB // CD} \right)\) có \(BC = 18{\rm{ cm,}}\,AD = 12{\rm{ cm}}\) . Điểm \(E\) thuộc cạnh \(AD\) sao cho \(AE = 6{\rm{ cm}}\) . Qua \(E\) kẻ đường thẳng song song với \(CD\) , cắt \(BC\) ở \(F\) . Tính độ dài \(BF\) .
-
A.
9 cm
-
B.
10 cm
-
C.
11 cm
-
D.
12 cm
Cho hình thang \(ABCD\,\left( {AB // CD} \right)\) . Một đường thẳng song song với \(AB\) cắt các cạnh bên \(AD,\,BC\) theo thứ tự ở \(E,\,F\) . Đẳng thức nào sau đây đúng?
-
A.
\(\frac{{ED}}{{AD}} + \frac{{BF}}{{BC}} = 1\)
-
B.
\(\frac{{AE}}{{AD}} + \frac{{BF}}{{BC}} = 1\)
-
C.
\(\frac{{AE}}{{ED}} + \frac{{BF}}{{FC}} = 1\)
-
D.
\(\frac{{AE}}{{ED}} + \frac{{FC}}{{BF}} = 1\)
Cho tam giác \(ABC\) có \(AM\) là trung tuyến và điểm \(E\) thuộc đoạn thẳng \(MC\) . Qua \(E\) kẻ đường thẳng song song với \(AC\) , cắt \(AB\) ở \(D\) và cắt \(AM\) ở \(K\) . Qua \(E\) kẻ đường thẳng song song với \(AB\) , cắt \(AC\) ở \(F\) . Hãy chọn khẳng định sai.
-
A.
\(\frac{{CF}}{{EF}} = \frac{{AC}}{{AB}}\)
-
B.
\(CF = DK\)
-
C.
\(\frac{{MG}}{{AG}} = \frac{{AB}}{{AC}}\)
-
D.
\(EF = AD\)
Cho tứ giác \(ABCD\) . Qua \(E \in AD\) kẻ đường thẳng song song với \(DC\) cắt \(AC\) ở \(G\) . Qua \(G\) kẻ đường thẳng song song với \(CB\) cắt \(AB\) tại \(H\) . Qua \(B\) kẻ đường thẳng song song với \(CD\) , cắt đường thẳng \(AC\) tại \(I\) . Qua \(C\) kẻ đường thẳng song song với \(BA\) , cắt \(BD\) tại \(F\) . Khẳng định nào sau đây là sai?
-
A.
\(IF // AD\)
-
B.
\(\frac{{OB}}{{OD}} = \frac{{OI}}{{OC}}\)
-
C.
\(\frac{{OF}}{{OB}} = \frac{{OC}}{{OA}}\)
-
D.
\(EH // BC\)
Cho hình thang \(ABCD\left( {AB // CD} \right)\) . \(M\) là trung điểm của \(CD\) . Gọi \(I\) là giao điểm của \(AM\) và \(BD\) , \(K\) là giao điểm của \(BM\) và \(AC\) . Đường thẳng \(IK\) cắt \(AD,\,BC\) theo thứ tự ở \(E\) và \(F\) . Có bao nhiêu khẳng định đúng trong các khẳng định sau?
(I) \(IK // AB\)
(II) \(EI = IK = KF\)
(III) \(\frac{{DI}}{{BD}} = \frac{{IM}}{{AM}}\)
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Cho tam giác \(ABC\) có đường cao \(AH\) . Trên \(AH\) lấy các điểm \(K,\,I\) sao cho \(AK = KI = IH\). Qua \(I,\,K\) lần lượt vẽ các đường thẳng \(EF // BC,\,MN // BC\) \(\left( {E,\,M \in AB;\,F,\,N \in AC} \right)\) . Cho biết diện tích của tam giác \(ABC\) là \(90\,{\rm{c}}{{\rm{m}}^2}\) . Hãy tính diện tích tứ giác \(MNF\) .
-
A.
\(30\,{\rm{c}}{{\rm{m}}^2}\)
-
B.
\(60\,{\rm{c}}{{\rm{m}}^2}\)
-
C.
\(90\,{\rm{c}}{{\rm{m}}^2}\)
-
D.
\(120\,{\rm{c}}{{\rm{m}}^2}\)
Cho đoạn thẳng \(ABC\) , điểm \(I\) nằm trong tam giác. Các tia \(AI,\,BI,CI\) cắt các cạnh \(BC,\,AC,\,AB\) theo thứ tự ở \(D,\,E,\,F\) . Tổng \(\frac{{AF}}{{FB}} + \frac{{AE}}{{EC}}\) bằng tỉ số nào dưới đây?
-
A.
\(\frac{{AI}}{{AD}}\)
-
B.
\(\frac{{AI}}{{ID}}\)
-
C.
\(\frac{{BD}}{{DC}}\)
-
D.
\(\frac{{DC}}{{DB}}\)
Lời giải và đáp án
Cho \(AB = 6\,{\rm{cm, }}AC = 18\,{\rm{cm}}\) , tỉ số hai đoạn thẳng \(AB\) và \(AC\) là:
-
A.
\(\frac{1}{2}\)
-
B.
\(\frac{1}{3}\)
-
C.
2
-
D.
3
Đáp án : B
Dựa vào định nghĩa tỉ số của hai đoạn thẳng: Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
\(AB = 6\,{\rm{cm, }}AC = 18\,{\rm{cm}}\)
Ta có \(\frac{{AB}}{{AC}} = \frac{6}{{18}} = \frac{1}{3}\)
-
A.
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow DE // BC\)
-
B.
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}} \Rightarrow DE // BC\)
-
C.
\(\frac{{AB}}{{BD}} = \frac{{AC}}{{EC}} \Rightarrow DE // BC\)
-
D.
\(\frac{{AD}}{{DE}} = \frac{{AE}}{{ED}} \Rightarrow DE // BC\)
Đáp án : D
Sử dụng định lý Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Theo định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Dễ thấy từ các điều kiện \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}};\,\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\,\frac{{AB}}{{BD}} = \frac{{AC}}{{EC}}\) ta đều có thể suy ra \(DE // BC\) .
Cho các đoạn thẳng \(AB = 6\,{\rm{cm,}}\,CD = 4\,{\rm{cm,}}\,PQ = 8\,{\rm{cm,}}\,EF = 10\,{\rm{cm,}}\) \(MN = 25{\rm{ mm, }}RS = 15\,{\rm{mm}}\) . Hãy chọn các phát biểu đúng trong các phát biểu sau:
-
A.
Hai đoạn thẳng \(AB\) và \(PQ\) tỉ lệ với hai đoạn thẳng \(EF\) và \(RS\) .
-
B.
Hai đoạn thẳng \(AB\) và \(RS\) tỉ lệ với hai đoạn thẳng \(EF\) và \(MN\) .
-
C.
Hai đoạn thẳng \(AB\) và \(CD\) tỉ lệ với hai đoạn thẳng \(PQ\) và \(EF\) .
-
D.
Cả 3 phát biểu đều sai.
Đáp án : B
Dựa vào định nghĩa tỉ số của hai đoạn thẳng: Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
\(MN = 25\,{\rm{mm}} = 2,5\,{\rm{cm; }}RS = 15{\rm{ mm}} = 1,5{\rm{ cm}}\)
\(\begin{array}{l}\left. \begin{array}{l}\frac{{AB}}{{PQ}} = \frac{6}{8} = \frac{3}{4}\\\frac{{EF}}{{RS}} = \frac{{10}}{{1,5}} = \frac{{20}}{3}\end{array} \right\} \Rightarrow \frac{{AB}}{{PQ}} \ne \frac{{EF}}{{RS}}\\\left. \begin{array}{l}\frac{{AB}}{{RS}} = \frac{6}{{1,5}} = 4\\\frac{{EF}}{{MN}} = \frac{{10}}{{2,5}} = 4\end{array} \right\} \Rightarrow \frac{{AB}}{{RS}} = \frac{{EF}}{{MN}}\\\left. \begin{array}{l}\frac{{AB}}{{CD}} = \frac{6}{4} = \frac{3}{2}\\\frac{{PQ}}{{EF}} = \frac{8}{{10}} = \frac{4}{5}\end{array} \right\} \Rightarrow \frac{{AB}}{{CD}} \ne \frac{{PQ}}{{EF}}\end{array}\)
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Đáp án : D
Sử dụng định lý Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
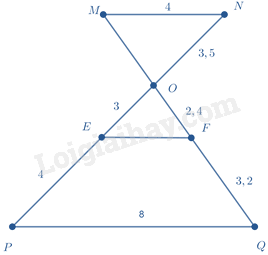
Ta có: \(\frac{{MN}}{{PQ}} = \frac{4}{8} = \frac{1}{2};\frac{{ON}}{{OP}} = \frac{{3,5}}{{3 + 4}} = \frac{1}{2} \Rightarrow \frac{{MN}}{{PQ}} = \frac{{ON}}{{OP}}\)
\( \Leftrightarrow MN // PQ\) (định lý Thalès đảo) (1)
Ta có: \(\frac{{OE}}{{PE}} = \frac{3}{4};\frac{{OF}}{{FQ}} = \frac{{2,4}}{{3,2}} = \frac{3}{4} \Rightarrow \frac{{OE}}{{PE}} = \frac{{OF}}{{FQ}}\)
\( \Rightarrow EF // PQ\) (định lý Thalès đảo) (2)
Từ (1), (2) \( \Rightarrow MN // EF\) (cùng song song với \(PQ\) ).
Vậy có 3 cặp đường thẳng song song.
Cho điểm \(C\) thuộc đoạn thẳng \(AB\) thỏa mãn \(\frac{{AC}}{{BC}} = \frac{3}{5}\) . Tính tỉ số \(\frac{{AC}}{{AB}}\) .
-
A.
\(\frac{1}{4}\)
-
B.
\(\frac{2}{5}\)
-
C.
\(\frac{3}{8}\)
-
D.
\(\frac{5}{8}\)
Đáp án : C
Dựa vào định nghĩa tỉ số của hai đoạn thẳng: Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
\(\begin{array}{l}\frac{{AC}}{{BC}} = \frac{3}{5} \Rightarrow AC = \frac{3}{5}BC \Rightarrow AB = AC + BC = \frac{3}{5}BC + BC = \frac{8}{5}BC\\ \Rightarrow \frac{{AC}}{{AB}} = \frac{{\frac{3}{5}BC}}{{\frac{8}{5}BC}} = \frac{3}{8}\end{array}\)
Cho các đoạn thẳng \(AB = 8{\rm{ cm, }}CD = 6{\rm{ cm, }}MN = 12{\rm{ cm, }}PQ = x{\rm{ cm}}\) . Tìm \(x\) để \(AB\) và \(CD\) tỉ lệ với \(MN\) và \(PQ\) .
-
A.
7 cm
-
B.
8 cm
-
C.
9 cm
-
D.
10 cm
Đáp án : C
Dựa vào định nghĩa hai đoạn thẳng tỉ lệ: Hai đoạn thẳng \(AB\) và \(CD\) gọi là tỉ lệ với hai đoạn thẳng \(A'B'\) và \(C'D'\) nếu có tỉ lệ thức: \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\) .
\(\begin{array}{l}\frac{{AB}}{{CD}} = \frac{8}{6} = \frac{4}{3}\\\frac{{MN}}{{PQ}} = \frac{{12}}{x}\\\frac{{AB}}{{CD}} = \frac{{MN}}{{PQ}} \Leftrightarrow \frac{4}{3} = \frac{{12}}{x} \Leftrightarrow x = \frac{{12.3}}{4} = 9\end{array}\)
-
A.
12
-
B.
21
-
C.
14
-
D.
15
Đáp án : B
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Xét tam giác \(ABC\) có \(DE // BC\) nên theo định lí Thalès ta có:
\(\begin{array}{l}\frac{{AD}}{{DB}} = \frac{{AE}}{{CE}} \Leftrightarrow \frac{{AD}}{{DB}} = \frac{{AC - CE}}{{CE}} \Leftrightarrow \frac{8}{6} = \frac{{AC - 9}}{9}\\ \Rightarrow AC - 9 = \frac{{8.9}}{6} = 12 \Rightarrow AC = 12 + 9 = 21\end{array}\)
-
A.
\(OM = 2,8\)
-
B.
\(OM = 1,8\)
-
C.
\(OM = 3,8\)
-
D.
\(OM = 0,8\)
Đáp án : A
Sử dụng định lý Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
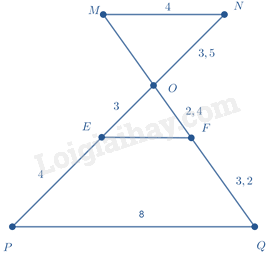
Ta có: \(\frac{{MN}}{{PQ}} = \frac{4}{8} = \frac{1}{2};\frac{{ON}}{{OP}} = \frac{{3,5}}{{3 + 4}} = \frac{1}{2} \Rightarrow \frac{{MN}}{{PQ}} = \frac{{ON}}{{OP}}\)
\( \Leftrightarrow MN // PQ\) (định lý Thalès đảo)
Theo hệ quả định lý Thalès ta có: \(\frac{{OM}}{{QO}} = \frac{{ON}}{{OP}} \Rightarrow OM = \frac{{QO.ON}}{{OP}} = \frac{{\left( {OF + FQ} \right)ON}}{{OE + EP}} = \frac{{\left( {2,4 + 3,2} \right)3,5}}{{3 + 4}} = 2,8\)
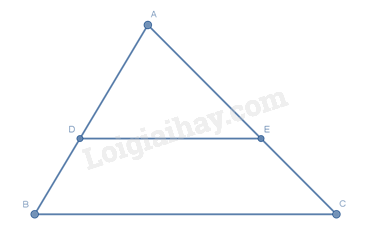
Cho tam giác \(ABC\) có \(AB = 12{\rm{ cm}}\) , điểm \(D\) thuộc cạnh \(AB\) sao cho \(AD = 8{\rm{ cm}}\) . Kẻ \(DE\) song song với \(BC\,\left( {E \in AC} \right)\) , kẻ \(EF\) song song với \(CD\,\left( {F \in AB} \right)\) . Tính độ dài \(AF\) .
-
A.
2 cm
-
B.
\(\frac{4}{3}\) cm
-
C.
3 cm
-
D.
\(\frac{{16}}{3}\) cm
Đáp án : D
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
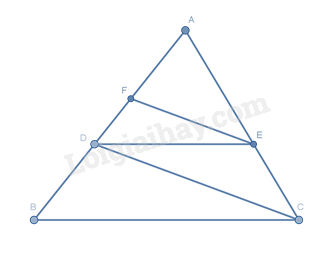
Xét tam giác \(ABC\) có \(DE // BC\) nên theo định lí Thalès ta có:
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) (1)
Xét tam giác \(ACD\) có \(EF // CD\) nên theo định lí Thalès ta có:
\(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}}\) (2)
Từ (1), (2) \( \Rightarrow \frac{{AD}}{{AB}} = \frac{{AF}}{{AD}} \Leftrightarrow AF.AB = A{D^2} \Rightarrow AF = \frac{{A{D^2}}}{{AB}} = \frac{{{8^2}}}{{12}} = \frac{{16}}{3}\)
Cho tứ giác \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Đường thẳng qua \(A\) và song song với \(BC\) cắt \(BD\) ở \(E\) . Đường thẳng qua \(B\) song song với \(AD\) cắt \(AC\) ở \(F\) . Chọn kết luận sai?
-
A.
\(\frac{{OE}}{{OB}} = \frac{{OA}}{{OC}}\)
-
B.
\(\frac{{EF}}{{AB}} = \frac{{OE}}{{OB}}\)
-
C.
\(\frac{{OB}}{{OD}} = \frac{{OF}}{{OA}}\)
-
D.
\(\frac{{OE}}{{OD}} = \frac{{OF}}{{OC}}\)
Đáp án : B
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
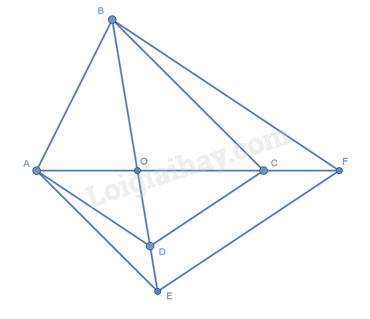
\(AE // BC\) nên theo hệ quả của định lí Thalès ta có: \(\frac{{OE}}{{OB}} = \frac{{OA}}{{OC}}\) (1)
\(BF // AD\) nên theo hệ quả của định lí Thalès ta có: \(\frac{{OB}}{{OD}} = \frac{{OF}}{{OA}}\) (2) Từ (1), (2) \( \Rightarrow \frac{{OE}}{{OB}} \cdot \frac{{OB}}{{OD}} = \frac{{OA}}{{OC}} \cdot \frac{{OF}}{{OA}}\) hay \(\frac{{OE}}{{OD}} = \frac{{OF}}{{OC}}\)
Cho tứ giác \(ABCD\) . Lấy điểm \(E\) bất kì thuộc \(BD\) . Qua \(E\) kẻ \(EF\) song song với \(AD\left( {F \in AB} \right)\) , kẻ \(EG\) song song với \(DC\,\left( {G \in BC} \right)\) . Chọn khẳng định sai:
-
A.
\(\frac{{BE}}{{ED}} = \frac{{BF}}{{FA}}\)
-
B.
\(FG // AC\)
-
C.
\(\frac{{BF}}{{FA}} = \frac{{BG}}{{GC}}\)
-
D.
\(FG // AD\)
Đáp án : D
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Sử dụng định lý Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
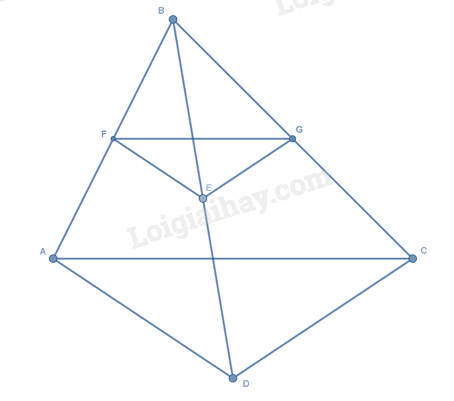
Xét tam giác \(ABD\) có \(EF // AD\) nên theo định lí Thalès ta có: \(\frac{{BF}}{{FA}} = \frac{{BE}}{{ED}}\) (1)
Xét tam giác \(BCD\) có \(EG // CD\) nên theo định lí Thalès ta có: \(\frac{{BE}}{{ED}} = \frac{{BG}}{{GC}}\) (2)
Từ (1), (2) \( \Rightarrow \frac{{BF}}{{FA}} = \frac{{BG}}{{GC}}\) do đó \(FG // AC\) (định lí Thalès đảo)
Cho điểm \(M\) thuộc đoạn thẳng \(AB\) sao cho \(MA = 2MB\) . Vẽ về một phía của \(AB\) các tam giác đều \(AMC\) và \(MBD\) . Gọi \(E\) là giao điểm của \(AD\) và \(MC\) , \(F\) là giao điểm của \(BC\) và \(DM\) . Đặt \(MB = a\) . Tính \(ME,MF\) theo \(a\) .
-
A.
\(ME = \frac{a}{2};MF = \frac{a}{3}\)
-
B.
\(ME = MF = \frac{{2a}}{3}\)
-
C.
\(ME = \frac{{2a}}{3};MF = \frac{a}{3}\)
-
D.
\(ME = MF = \frac{a}{3}\)
Đáp án : B
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

\(MB = a \Rightarrow MA = 2a\)
Vì các tam giác \(AMC\) và \(MBD\) đều nên \(\widehat {MAC} = \widehat {BMD} = 60^\circ \) .
Mà 2 góc này ở vị trí đồng vị \( \Rightarrow MD // AC\)
Vì \(MD // AC\) nên theo hệ quả định lí Thalès cho hai tam giác \(DEM\) và \(ACE\) có \(\frac{{ME}}{{EC}} = \frac{{MD}}{{AC}}\)
Mà \(MD = MB\) và \(AC = MA\) nên \(\frac{{ME}}{{EC}} = \frac{{MD}}{{AC}} = \frac{{MB}}{{MA}} = \frac{1}{2}\)
\( \Rightarrow \frac{{ME}}{{EC}} = \frac{1}{2} \Rightarrow \frac{{ME}}{{ME + EC}} = \frac{1}{{1 + 2}} = \frac{1}{3}\)
\( \Rightarrow \frac{{ME}}{{2a}} = \frac{1}{3} \Rightarrow ME = \frac{{2a}}{3}\)
Tương tự, \(MF = \frac{{2a}}{3}\)
Vậy \(ME = MF = \frac{{2a}}{3}\)
Cho hình thang \(ABCD\left( {AB // CD} \right)\) có diện tích \(48\,{\rm{c}}{{\rm{m}}^2}\) , \(AB = 4\,{\rm{cm,}}\,CD = 8{\rm{cm}}\) . Gọi \(O\) là giao điểm của hai đường chéo. Tính diện tích tam giác \(COD\)
-
A.
\(\frac{{64}}{3}{\rm{c}}{{\rm{m}}^2}\)
-
B.
\({\rm{15c}}{{\rm{m}}^2}\)
-
C.
\({\rm{16c}}{{\rm{m}}^2}\)
-
D.
\({\rm{32c}}{{\rm{m}}^2}\)
Đáp án : A
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
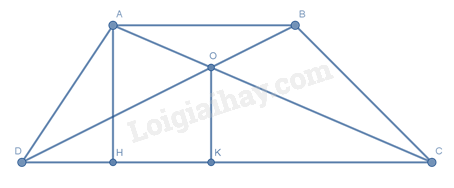
Kẻ \(AH \bot DC;\,OK \bot DC\) tại \(H,\,K\) \( \Rightarrow AH \bot OK\) .
Chiều cao của hình thang \(AH = \frac{{2{S_{ABCD}}}}{{AB + CD}} = \frac{{2.48}}{{4 + 8}} = 8\) (cm)
Vì \(AB // CD\) ( \(ABCD\) là hình thang) nên theo hệ quả định lí Thalès ta có \(\frac{{OC}}{{OA}} = \frac{{CD}}{{AB}} = \frac{8}{4} = 2\)
\(\begin{array}{l} \Rightarrow \frac{{OC}}{{OA + OC}} = \frac{2}{{2 + 1}}\\ \Rightarrow \frac{{OC}}{{AC}} = \frac{2}{3}\end{array}\)
Vì \(AH // OK\) nên theo hệ quả định lý Thalès ta có \(\frac{{OK}}{{AH}} = \frac{{OC}}{{AC}} = \frac{2}{3} \Rightarrow OK = \frac{2}{3}AH = \frac{2}{3} \cdot 8 = \frac{{16}}{3}\) (cm)
Do đó \({S_{COD}} = \frac{1}{2}OK.DC = \frac{1}{2} \cdot \frac{{16}}{3} \cdot 8 = \frac{{64}}{3}\,{\rm{c}}{{\rm{m}}^2}\) .
Cho hình thang \(ABCD\,\left( {AB // CD} \right)\) có \(BC = 18{\rm{ cm,}}\,AD = 12{\rm{ cm}}\) . Điểm \(E\) thuộc cạnh \(AD\) sao cho \(AE = 6{\rm{ cm}}\) . Qua \(E\) kẻ đường thẳng song song với \(CD\) , cắt \(BC\) ở \(F\) . Tính độ dài \(BF\) .
-
A.
9 cm
-
B.
10 cm
-
C.
11 cm
-
D.
12 cm
Đáp án : A
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
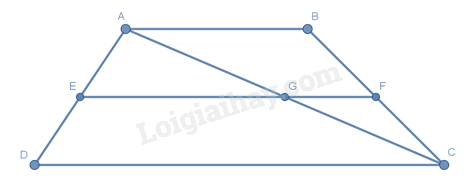
\(\left. \begin{array}{l}AB // CD\\EF // CD\end{array} \right\} \Rightarrow AB // EF\)
Gọi \(G\) là giao điểm của \(EF\) và \(AC\) \( \Rightarrow \left\{ \begin{array}{l}EG // CD\\GF // AB\end{array} \right.\)
Xét tam giác \(ACD\) có \(EG // CD\) nên theo định lí Thalès ta có:
\(\frac{{CG}}{{AG}} = \frac{{DE}}{{AE}} = \frac{{AD - AE}}{{AE}} = \frac{{12 - 6}}{6} = 1\)
Xét tam giác \(ABC\) có \(GF // AB\) nên theo định lí Thalès ta có:
\(\frac{{CF}}{{BF}} = \frac{{CG}}{{AG}} = 1 \Rightarrow BF = CF = \frac{{BC}}{2} = \frac{{18}}{2} = 9{\rm{ cm}}\)
Cho hình thang \(ABCD\,\left( {AB // CD} \right)\) . Một đường thẳng song song với \(AB\) cắt các cạnh bên \(AD,\,BC\) theo thứ tự ở \(E,\,F\) . Đẳng thức nào sau đây đúng?
-
A.
\(\frac{{ED}}{{AD}} + \frac{{BF}}{{BC}} = 1\)
-
B.
\(\frac{{AE}}{{AD}} + \frac{{BF}}{{BC}} = 1\)
-
C.
\(\frac{{AE}}{{ED}} + \frac{{BF}}{{FC}} = 1\)
-
D.
\(\frac{{AE}}{{ED}} + \frac{{FC}}{{BF}} = 1\)
Đáp án : A
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
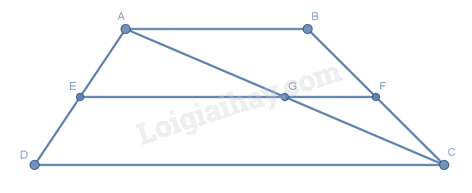
\(\left. \begin{array}{l}AB // CD\\EF // CD\end{array} \right\} \Rightarrow AB // EF\)
Gọi \(G\) là giao điểm của \(EF\) và \(AC\) \( \Rightarrow \left\{ \begin{array}{l}EG // CD\\GF // AB\end{array} \right.\)
Xét tam giác \(ACD\) có \(EG // CD\) nên theo định lí Thalès ta có:
\(\frac{{DE}}{{AD}} = \frac{{CG}}{{AC}}\) (1)
Xét tam giác \(ABC\) có \(FG // AB\) nên theo định lí Thalès ta có:
\(\frac{{CG}}{{AC}} = \frac{{CF}}{{BC}}\) (2)
Từ (1), (2) \( \Rightarrow \frac{{DE}}{{AD}} = \frac{{CF}}{{BC}} \Rightarrow \frac{{DE}}{{AD}} + \frac{{BF}}{{BC}} = \frac{{CF}}{{BC}} + \frac{{BF}}{{BC}} = \frac{{CF + BF}}{{BC}} = \frac{{BC}}{{BC}} = 1\)
Cho tam giác \(ABC\) có \(AM\) là trung tuyến và điểm \(E\) thuộc đoạn thẳng \(MC\) . Qua \(E\) kẻ đường thẳng song song với \(AC\) , cắt \(AB\) ở \(D\) và cắt \(AM\) ở \(K\) . Qua \(E\) kẻ đường thẳng song song với \(AB\) , cắt \(AC\) ở \(F\) . Hãy chọn khẳng định sai.
-
A.
\(\frac{{CF}}{{EF}} = \frac{{AC}}{{AB}}\)
-
B.
\(CF = DK\)
-
C.
\(\frac{{MG}}{{AG}} = \frac{{AB}}{{AC}}\)
-
D.
\(EF = AD\)
Đáp án : C
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
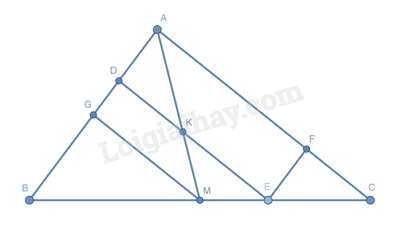
Xét tứ giác \(ADEF\) có: \(\left\{ \begin{array}{l}DE // AF\left( {DE // AC,\,F \in AC} \right)\\EF // AD\left( {EF // AB,\,D \in AB} \right)\end{array} \right.\) nên \(ADEF\) là hình bình hành.
\( \Rightarrow EF = AD\) (1)
Kẻ \(MG // AC\,\left( {G \in AB} \right)\) .
Xét tam giác \(ABC\) có: \(MG // AC\) nên theo định lí Thalès ta có \(\frac{{BG}}{{AG}} = \frac{{BM}}{{CM}} = 1 \Rightarrow BG = AG\) hay \(G\) là trung điểm của \(AB\) .
Xét tam giác \(ABC\) có \(EF // AB\) nên theo định lí Thalès ta có \(\frac{{CF}}{{AC}} = \frac{{EF}}{{AB}}\) hay \(\frac{{CF}}{{EF}} = \frac{{AC}}{{AB}}\) (2)
Tương tự với tam giác \(AGM\) và tam giác \(ABC\) có \(\frac{{DK}}{{AD}} = \frac{{MG}}{{AG}} = \frac{{MG}}{{BG}} = \frac{{AC}}{{AB}}\) (3)
Từ (1), (2), (3) \( \Rightarrow CF = DK\) .
Cho tứ giác \(ABCD\) . Qua \(E \in AD\) kẻ đường thẳng song song với \(DC\) cắt \(AC\) ở \(G\) . Qua \(G\) kẻ đường thẳng song song với \(CB\) cắt \(AB\) tại \(H\) . Qua \(B\) kẻ đường thẳng song song với \(CD\) , cắt đường thẳng \(AC\) tại \(I\) . Qua \(C\) kẻ đường thẳng song song với \(BA\) , cắt \(BD\) tại \(F\) . Khẳng định nào sau đây là sai?
-
A.
\(IF // AD\)
-
B.
\(\frac{{OB}}{{OD}} = \frac{{OI}}{{OC}}\)
-
C.
\(\frac{{OF}}{{OB}} = \frac{{OC}}{{OA}}\)
-
D.
\(EH // BC\)
Đáp án : D
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

\(\left. \begin{array}{l}EG // DC \Rightarrow \frac{{AE}}{{AD}} = \frac{{AG}}{{AC}}\\GH // BC \Rightarrow \frac{{AG}}{{AC}} = \frac{{AH}}{{AB}}\end{array} \right\} \Rightarrow \frac{{AE}}{{AD}} = \frac{{AH}}{{AB}} \Rightarrow EH // BD\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD\) .
\(\left. \begin{array}{l}BI // DC \Rightarrow \frac{{OI}}{{OC}} = \frac{{OB}}{{OD}}\\AB // CF \Rightarrow \frac{{OC}}{{OA}} = \frac{{OF}}{{OB}}\end{array} \right\} \Rightarrow \frac{{OI}}{{OA}} = \frac{{OF}}{{OD}} \Rightarrow AD // IF\)
Cho hình thang \(ABCD\left( {AB // CD} \right)\) . \(M\) là trung điểm của \(CD\) . Gọi \(I\) là giao điểm của \(AM\) và \(BD\) , \(K\) là giao điểm của \(BM\) và \(AC\) . Đường thẳng \(IK\) cắt \(AD,\,BC\) theo thứ tự ở \(E\) và \(F\) . Có bao nhiêu khẳng định đúng trong các khẳng định sau?
(I) \(IK // AB\)
(II) \(EI = IK = KF\)
(III) \(\frac{{DI}}{{BD}} = \frac{{IM}}{{AM}}\)
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Đáp án : D
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Sử dụng định lý Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
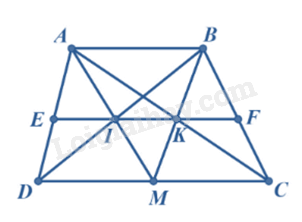
\(\left. \begin{array}{l}AB // DM \Rightarrow \frac{{IM}}{{IA}} = \frac{{MD}}{{AB}}\\AB // MC \Rightarrow \frac{{MK}}{{KB}} = \frac{{MC}}{{AB}}\end{array} \right\} \Rightarrow \frac{{IM}}{{IA}} = \frac{{MK}}{{KB}} \Rightarrow IK // AB\)
\(\left. \begin{array}{l}AB // EI \Rightarrow \frac{{IE}}{{AB}} = \frac{{ID}}{{DB}}\\AB // IK \Rightarrow \frac{{IK}}{{AB}} = \frac{{IM}}{{MA}}\\AB // DM \Rightarrow \frac{{DI}}{{BI}} = \frac{{IM}}{{IA}} \Rightarrow \frac{{DI}}{{BD}} = \frac{{IM}}{{AM}}\end{array} \right\} \Rightarrow \frac{{IE}}{{AB}} = \frac{{IK}}{{AB}} \Rightarrow EI = IK\)
Tương tự, \(IK = KF\) . Do đó \(EI = IK = KF\) .
Cho tam giác \(ABC\) có đường cao \(AH\) . Trên \(AH\) lấy các điểm \(K,\,I\) sao cho \(AK = KI = IH\). Qua \(I,\,K\) lần lượt vẽ các đường thẳng \(EF // BC,\,MN // BC\) \(\left( {E,\,M \in AB;\,F,\,N \in AC} \right)\) . Cho biết diện tích của tam giác \(ABC\) là \(90\,{\rm{c}}{{\rm{m}}^2}\) . Hãy tính diện tích tứ giác \(MNF\) .
-
A.
\(30\,{\rm{c}}{{\rm{m}}^2}\)
-
B.
\(60\,{\rm{c}}{{\rm{m}}^2}\)
-
C.
\(90\,{\rm{c}}{{\rm{m}}^2}\)
-
D.
\(120\,{\rm{c}}{{\rm{m}}^2}\)
Đáp án : A
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
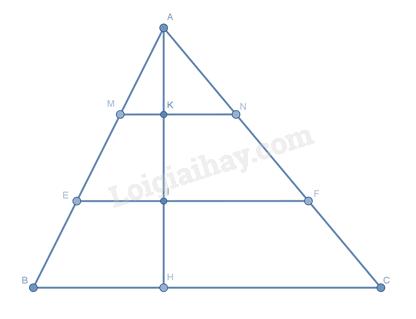
Ta có \(AK = KI = IH\) và \(AK + KI + IH = 3.KI = AH\) nên \( KI = \frac{1}{3}AH\)
Vì \(MN // BC \) nên \( \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} \) nên \( \frac{{MN}}{{BC}} = \frac{1}{3}\) suy ra \(MN = \frac{1}{3}BC \)
Vì \(EF // BC \) nên \( \frac{{EF}}{{BC}} = \frac{{AF}}{{AC}} \) nên \( \frac{{EF}}{{BC}} = \frac{2}{3}\) suy ra \(FE = \frac{2}{3}BC\)
\(MNFE\) có \(MN // FE\) và \(KI \bot MN\). Do đó \(MNEF\) là hình thang có 2 đáy \(MN,\,FE\) , chiều cao \(KI\) .
\( \) nên \( {S_{MNEF}} = \frac{{\left( {MN + FE} \right)KI}}{2} = \frac{{\left( {\frac{1}{3}BC + \frac{2}{3}BC} \right) \cdot \frac{1}{3}AH}}{2} = \frac{1}{3}{S_{ABC}} = 30\,{\rm{c}}{{\rm{m}}^2}\)
Cho đoạn thẳng \(ABC\) , điểm \(I\) nằm trong tam giác. Các tia \(AI,\,BI,CI\) cắt các cạnh \(BC,\,AC,\,AB\) theo thứ tự ở \(D,\,E,\,F\) . Tổng \(\frac{{AF}}{{FB}} + \frac{{AE}}{{EC}}\) bằng tỉ số nào dưới đây?
-
A.
\(\frac{{AI}}{{AD}}\)
-
B.
\(\frac{{AI}}{{ID}}\)
-
C.
\(\frac{{BD}}{{DC}}\)
-
D.
\(\frac{{DC}}{{DB}}\)
Đáp án : B
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
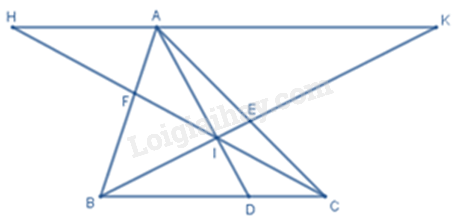
Qua \(A\) kẻ đường thẳng song song với \(BC\) cắt \(CF,\,BE\) lần lượt tại \(H,K\) .
\(AH // BC\) nên theo hệ quả định lí Thalès ta có \(\frac{{AF}}{{BF}} = \frac{{AH}}{{BC}}\)
\(AK // BC\) nên theo hệ quả định lí Thalès ta có \(\frac{{AE}}{{EC}} = \frac{{AK}}{{BC}}\)
\( \Rightarrow \frac{{AF}}{{BF}} + \frac{{AE}}{{EC}} = \frac{{AH}}{{BC}} + \frac{{AK}}{{BC}} = \frac{{HK}}{{BC}}\) (1)
Lại có \(AH // DC\) nên theo định lí Thalès ta có \(\frac{{AI}}{{ID}} = \frac{{AH}}{{CD}}\)
\(AK // BD\) nên theo định lí Thalès ta có \(\frac{{AI}}{{ID}} = \frac{{AK}}{{BD}}\)
Do đó \(\frac{{AI}}{{ID}} = \frac{{AH}}{{CD}} = \frac{{AK}}{{BD}}\) (2)
Theo tính chất dãy tỉ số bằng nhau \(\frac{{AH}}{{CD}} = \frac{{AK}}{{BD}} = \frac{{AH + AK}}{{CD + BD}} = \frac{{HK}}{{BC}}\) (3)
Từ (2) và (3) \( \Rightarrow \frac{{AI}}{{ID}} = \frac{{HK}}{{BC}}\) (4)
Từ (1) và (4) \( \Rightarrow \frac{{AF}}{{BF}} + \frac{{AE}}{{EC}} = \frac{{AI}}{{ID}}\)