Trắc nghiệm vật lí 11 bài 13 kết nối tri thức có đáp án — Không quảng cáo

Sóng dừng trên sợi dây hai đầu cố định nên chiều dài dây thỏa mãn \(l = k\frac{\lambda }{2}\)

Vì trên dây có 5 nút sóng kể cả 2 đầu nên k = 4 do đó \(l = 4\frac{\lambda }{2} \Rightarrow \lambda  = {\rm{0}},5m\)

Đáp án A.

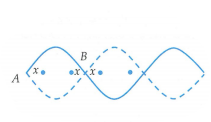
- Các điểm dao động cùng biên độ khi các điểm đó cách nút một khoảng như nhau.

- Giả sử những điểm dao động cùng biên độ cách nút một khoảng x, \(x \le \frac{\lambda }{4}\).

- Vì các điểm này có vị trí cân bằng liên tiếp và cách đều nhau, nên từ hình vẽ, ta có: \(\left\{ \begin{array}{l}x + d + x = \frac{\lambda }{2}\\x + x = d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}d = \frac{\lambda }{4}\\x = \frac{\lambda }{8}\end{array} \right.\)

Vì A ₁ > A ₂ > 0 nên ta có

+ Khi \(x = \frac{\lambda }{8}\) thì ta có những điểm có cùng biên độ A ₂ và có vị trí cân bằng cách đều nhau một khoảng \({d_2} = \frac{\lambda }{4}\)

Khi \(x = \frac{\lambda }{4}\) thì ta có những điểm cùng biên độ A ₁ (điểm bụng) và có vị trí cân bằng cách đều nhau một khoảng \({d_1} = 2x = \frac{\lambda }{2}\)

\(\left\{ \begin{array}{l}{d_1} = \frac{\lambda }{2}\\{d_2} = \frac{\lambda }{2}\end{array} \right. \Rightarrow \frac{{{d_1}}}{{{d_2}}} = \frac{{\frac{\lambda }{2}}}{{\frac{\lambda }{4}}} = 2 \Rightarrow {d_1} = 2{d_2}\)

Đáp án D.

Vì M và N dao động ngược pha nên M và N đối xứng với nhau qua nút Q nào đó, còn N và P đối xứng nhau qua bụng. Gọi nút gần P nhất là R.

Do 3 điểm này cùng biên độ nên từ công thức biên độ \(A = 2a\left| {\sin \frac{{2\pi d}}{\lambda }} \right|\) (d là khoảng cách từ điểm xét tới nút) ta suy ra \(QM = QN = PR = \frac{{MN}}{2} = {\rm{0}},5cm\) .

Mặt khác ta có khoảng cách giữa hai nút QR là

\(QR = \frac{\lambda }{2} \Rightarrow QN + NP + PR = \frac{\lambda }{2} \Rightarrow \frac{\lambda }{2} \Rightarrow {\rm{0}},5 + 2 + {\rm{0}},5 = \frac{\lambda }{2} \Rightarrow \lambda  = 6\)

Khoảng thời gian giữa hai lần sợi dây duỗi thẳng là \(\frac{T}{2} = {\rm{0}},{\rm{04}} \Rightarrow T = 0,08\)

\( \Rightarrow \omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{{{\rm{0}},{\rm{0}}8}} \Rightarrow {v_{\max }} = A\omega  = 8.1{{\rm{0}}^{ - 3}}.\frac{{2\pi }}{{{\rm{0,0}}8}} = {\rm{0}},628m/s = 628mm/s\)

Đáp án D.

Khi tần số là f ₁ thì: \(l = \left( {{n_1} - 1} \right)\frac{{{\lambda _1}}}{2} = \left( {{n_1} - 1} \right)\frac{v}{{2{f_1}}}\left( 1 \right)\)

Khi tần số là f ₂ thì: \(l = \left( {{n_2} - 1} \right)\frac{{{\lambda _2}}}{2} = \left( {{n_2} - 1} \right)\frac{v}{{2{f_2}}}\left( 2 \right)\)

Từ (1) và (2) ta có: \(l = \left( {{n_1} - 1} \right)\frac{{{\lambda _2}}}{{2{f_1}}} = \left( {{n_2} - 1} \right)\frac{v}{{2{f_2}}} \Leftrightarrow \frac{{\left( {{n_1} - 1} \right)}}{{{f_1}}} = \frac{{\left( {{n_2} - 1} \right)}}{{{f_2}}}\)

Thay số ta được \(\frac{{16 - 1}}{{5{\rm{0}}}} = \frac{{1{\rm{0}} - 1}}{{{f_2}}} \Rightarrow {f_2} = 3{\rm{0}}Hz.\)

Đáp án A.

Trong phần lí thuyết ta đã chứng minh khoảng thời gian giữa hai lần sợi dây duỗi thẳng là: \(\frac{T}{2} = {\rm{0}},6 \Rightarrow T = 1,2s\)

Trên sợi dây hình thành ra 5 nút sóng, trong đó có 2 nút nằm tại hai đầu sợi dây, vì vậy có 4 bụng sóng trên sợi dây và chiều dài sợi dây là:

\(l = 4\frac{\lambda }{2} = 36cm \Rightarrow \lambda  = 18cm\)

Vận tốc truyền sóng trên sợi dây là: \(v = \frac{\lambda }{T} = \frac{{18}}{{1,2}} = 15cm/s\)

Đáp án C.

Gọi vận tốc truyền sóng trên sợi dây là v, do hai đầu dây cố định nên ta có:

Khi tần số là f ₁ , trên dây xuất hiện n ₁ bó sóng nên \(l = {n_1}\frac{{{\lambda _1}}}{2} = {n_1}\frac{v}{{2{f_1}}}\left( 1 \right)\)

Khi tần số là f ₂ , trên dây xuất hiện n ₂ bó sóng nên \(l = {n_2}\frac{{{\lambda _2}}}{2} = {n_2}\frac{v}{{2{f_2}}}\left( 2 \right)\)

Từ (1) và (2) ta có: \(l = {n_1}\frac{{{\lambda _1}}}{2} = {n_2}\frac{{{\lambda _2}}}{2} \Leftrightarrow \frac{{{f_1}}}{{{f_2}}} = \frac{{{n_1}}}{{{n_2}}} \Leftrightarrow \frac{{45}}{{54}} = \frac{{{n_1}}}{{{n_2}}} = \frac{5}{6}\left( 3 \right)\)

Do f ₁ và f ₂ là hai tần số liên tiếp xảy ra sóng dừng trên sợi dây, nên số bó sóng trong hai trường hợp chỉ hơn kém nhau 1 đơn vị (tức n ₁ , n ₂ là hai số nguyên liên tiếp). Từ (3) suy ra n ₁ = 5 bó sóng; n ₂ = 6 bó sóng.

Giả sử với tần số f thì lúc đó sợi dây xuất hiện n bó sóng, khi đó: \(l = n\frac{\lambda }{2} = n\frac{v}{{2f}}\left( 4 \right)\)

Từ (1) và (4), ta có: \(l = n\frac{v}{{2{f_1}}} = n\frac{v}{{2f}} \Leftrightarrow \frac{{{n_1}}}{{{f_1}}} = \frac{n}{f} \Rightarrow f = \frac{{n{f_1}}}{{{n_1}}} = \frac{{n.45}}{5} = 9n\)

Để tần số f nhỏ nhất thì n nguyên nhỏ nhất, suy ra n = 1, ta có f _min = 9.1 = 9 Hz.

Đáp án A.

Giả sử khi tần số dao động là f ₁ thì số nút trên dây là n ₁ , khi đó:

\(l = \left( {{n_1} - 1} \right)\frac{1}{2} = \left( {{n_1} - 1} \right)\frac{v}{{2{f_1}}}\left( 1 \right)\)

Tốc độ truyền sóng trên dây: \(v = 2l\frac{{{f_1}}}{{\left( {{n_1} - 1} \right)}}\left( 2 \right)\)

Giả sử khi tần số dao động là f ₂ thì số nút trên dây là n ₂ =  n ₁ - 8, khi đó:

\(l = \left( {{n_2} - 1} \right)\frac{1}{2} = l = \left( {{n_2} - 1} \right)\frac{v}{{2{f_2}}}\left( 3 \right)\)

Từ (1) và (3), ta có:

\(l = \left( {{n_1} - 1} \right)\frac{v}{{2{f_1}}} = \left( {{n_2} - 1} \right)\frac{v}{{2{f_2}}} \Leftrightarrow \frac{{{n_1} - 1}}{{{f_1}}} = \frac{{{n_2} - 1}}{{{f_2}}} = \frac{{\left( {{n_2} - 1} \right)\left( {{n_1} - 1} \right)}}{{{f_2} - {f_1}}} = \frac{{{n_2} - {n_1}}}{{{f_2} - {f_1}}} = \frac{8}{{4{\rm{0}}}} = \frac{1}{5}\)

Thay vào (2) ta được: \(v = 2l\frac{{{f_1}}}{{\left( {{n_1} - 1} \right)}} = 2l.5 = 1{\rm{0}}l\)

Thời gian sóng truyền đi giữa hai đầu dây: \(t = \frac{l}{v} = \frac{l}{{1{\rm{0}}l}} = {\rm{0}},1s\)

Đáp án A.

Bước sóng: \(\lambda  = \frac{v}{f} = \frac{{12{\rm{0}}}}{{2{\rm{0}}}}cm\)

Xét một điểm M trên sợi dây, cách đầu dây một đoạn x, tại M có bụng sóng khi:

\({\rm{0}} \le x = \left( {2k + 1} \right)\frac{\lambda }{4} \le l \Leftrightarrow {\rm{0}} \le 2k + 1 \le \frac{{4l}}{\lambda } = \frac{{4.22,1}}{6} = 14,73 \Leftrightarrow  - \frac{1}{2} \le k \le 687\)

\( \Rightarrow k = {\rm{0}};1;2;3;4;5;6\)

Có 7 giá trị của k nên có 7 điểm bụng trên sợi dây.

Xét một điểm M trên sợi dây, cách đầu dây một đoạn x, tại M có nút sóng khi:

\({\rm{0}} \le x = k\frac{\lambda }{2} \le l \Leftrightarrow {\rm{0}} \le k \le \frac{{2l}}{\lambda } = \frac{{2.22,1}}{6} = 7,37 \Rightarrow k = {\rm{0}};1;2;3;4;5;6;7\)

Có 8giá trị của k nên có 8 điểm nút trên sợi dây.

Đáp án C.

Đối với sóng dừng, trừ những điểm nút đứng yên không dao động, những điểm dao động còn lại sẽ hoặc đồng pha với nhau và ngược pha với những điểm còn lại. Cụ thể những điểm nằm bên trên vị trí cân bằng thì luôn đồng pha với nhau và ngược pha với những điểm nằm bên dưới vị trí cân bằng. Chọn trục tọa trùng với sợi dây, gốc tọa độ trùng vào điểm O, chiều dương hướng sang phải.

Xét những điểm nằmvề một phía của điểm O, những điểm có tọa độ \(2k\frac{\lambda }{2} \le x \le \left( {2k + 1} \right)\frac{\lambda }{2}\) thì luôn dao động đồng pha với nhau và ngược pha với những điểm có tọa độ \(\left( {2k + 1} \right)\frac{\lambda }{2} \le x \le 2k\frac{\lambda }{2}\)

Kiểm tra tọa độ của các điểm, ta có:

Điểm M có: \(7\frac{\lambda }{2} \le {x_M} = 59 = 7,375\frac{\lambda }{2} \le 8\frac{\lambda }{2}\)

Điểm N có: \(1{\rm{0}}\frac{\lambda }{2} \le {x_N} = 87 = 1{\rm{0}},875\frac{\lambda }{2} \le 11\frac{\lambda }{2}\)

Điểm P có: \(13\frac{\lambda }{2} \le {x_P} = 1{\rm{0}}6 = 13,25\frac{\lambda }{2} \le 14\frac{\lambda }{2}\)

Điểm Q có: \(18\frac{\lambda }{2} \le {x_Q} = 147 = 18,375\frac{\lambda }{2} \le 19\frac{\lambda }{2}\)

Kết luận: Các điểm M và P đồng pha với nhau và ngược pha với các điểm N và Q.

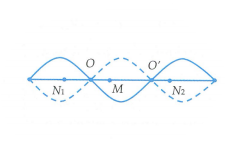
Tần số dao động: \(f = \frac{\omega }{{2\pi }} = \frac{{2{\rm{0}}\pi }}{{2\pi }} = 1{\rm{0}}Hz\)

Bước sóng: \(\lambda  = \frac{v}{f} = \frac{{24{\rm{0}}}}{{1{\rm{0}}}} = 24cm\)

Xét bốn điểm thuộc 3 bó sóng liên tiếp theo thứ tự: Điểm N ₁ thuộc bó sóng thứ nhất - nút O - điểm M gần O nhất thuộc bó sóng thứ 2 - nút O'- điểm N ₂ thuộc bó sóng thứ ba (hình vẽ).

Do biên độ dao động tại M là \({A_M} = \frac{{{A_{\rm{0}}}}}{{\sqrt 2 }}\) nên khoảng cách ngắn nhất từ M tới nút O là: \(MO = \frac{\lambda }{8} = 3cm\)

Với điểm N ₁ nằm bên trái điểm M, ta có \({N_1}O = {N_1}M - MO = 11 - 3 = 8cm\):

\({A_{{N_1}}} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{{N_1}O}}{\lambda }} \right| = \left| {{A_{\rm{0}}}\sin 2\pi \frac{8}{{24}}} \right| = \frac{{{A_{\rm{0}}}\sqrt 3 }}{2}\)

Điểm N ₁ đồng pha với điểm M nên phương trình dao động của điểm N ₁ là:

\({u_{{N_1}}} = \frac{{{A_{\rm{0}}}\sqrt 3 }}{2}\cos \left( {2{\rm{0}}\pi t + \frac{\pi }{4} - \pi } \right) = \frac{{{A_{\rm{0}}}\sqrt 3 }}{2}\cos \left( {2{\rm{0}}\pi t - \frac{{3\pi }}{4}} \right)\)

Với điểm N ₂ nằm bên phải điểm M, ta có: \({N_2}O' = {N_2}M - MO' = 11 - 9 = 2cm\)

\({A_{{N_2}}} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{{N_2}O'}}{\lambda }} \right| = \left| {{A_{\rm{0}}}\sin 2\pi \frac{2}{{24}}} \right| = \frac{{{A_{\rm{0}}}}}{2}\)

Điểm N ₂ đồng pha với điểm M nên phương trình dao động của điểm N ₂ là:

\({u_{{N_1}}} = \frac{{{A_{\rm{0}}}}}{2}\cos \left( {2{\rm{0}}\pi t - \frac{{3\pi }}{4}} \right)\)

Đáp án B.

Gọi x ₁ ,x ₂ là khoảng cách từ M và N tới đầu nút cố định, ta có:

\({x_1} - {x_2} = 3,75\lambda  \Rightarrow {x_1} = {x_2} + 3,75\lambda \)

Gọi A ₀ = 2a là biên độ tại bụng sóng, biên độ sóng dừng tại M và N tương ứng là:

\({A_M} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{{x_1}}}{\lambda }} \right| \Rightarrow \left| {\sin 2\pi \frac{{{x_1}}}{\lambda }} \right| = \frac{{{A_M}}}{{{A_{\rm{0}}}}}\)

\({A_N} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{{x_1} - 3,75\lambda }}{\lambda }} \right| = \left| {{A_{\rm{0}}}\sin \left( {2\pi \frac{{{x_1}}}{\lambda } - 7,5\pi } \right)} \right| = \left| {{A_{\rm{0}}}\cos \left( {2\pi \frac{{{x_1}}}{\lambda }} \right)} \right|\)

\( \Rightarrow \left| {\cos \left( {2\pi \frac{{{x_1}}}{\lambda }} \right)} \right| = \frac{{{A_N}}}{{{A_{\rm{0}}}}}\)

Do đó ta có \(\sin 2\pi \frac{{{x_1}}}{\lambda } + {\cos ^2}2\pi \frac{{{x_1}}}{\lambda } = {\left( {\frac{{{A_M}}}{{{A_{\rm{0}}}}}} \right)^2} + {\left( {\frac{{{A_N}}}{{{A_{\rm{0}}}}}} \right)^2} = \frac{{A_M^2 + A_N^2}}{{A_{\rm{0}}^2}} = 1\)

\( \Rightarrow {A_{\rm{0}}} = 2a = \sqrt {A_M^2 + A_N^2}  = \sqrt {{6^2} + {8^2}}  = 1{\rm{0}} \Rightarrow a = 5cm\)

Đáp án D.

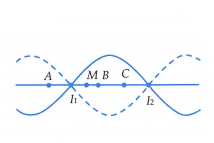
Theo bài ra vị trí của ba điểm A, B, C được thể hiện như hình vẽ.

Do biên độ của ba điểm A, B, C bằng nhau nên khoảng cách từ mỗi điểm này đến mỗi nút gần nó nhất phải bằng nhau. Ta có:

\(\left\{ \begin{array}{l}A{I_1} = B{I_1} = C{I_2}\\AC = A{I_1} + {I_1}C = C{I_2} + {I_1}C = {I_1}{I_2} = \frac{\lambda }{2}\end{array} \right.\)

Ta có: \(AC = AB + BC = AB + \frac{{AB}}{2} = \frac{{3AB}}{2} = \frac{\lambda }{2} \Rightarrow \left\{ \begin{array}{l}AB = \frac{\lambda }{3}\\A{I_1} = \frac{\lambda }{6}\end{array} \right.\)

Gọi \({A_{\rm{0}}} = 2a\) là biên độ tại bụng sóng, biên độ dao động tại điểm A là:

\({A_A} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{\frac{\lambda }{6}}}{\lambda }} \right| = \left| {{A_{\rm{0}}}\sin \frac{\pi }{3}} \right| = \frac{{{A_{\rm{0}}}\sqrt 3 }}{2} = 4\sqrt 3  \Rightarrow {A_{\rm{0}}} = 8\)

Khoảng cách từ M tới điểm nút I ₁ là: \(M{I_1} = MA - {I_1}A = \frac{{AC}}{2} - {I_1}A = \frac{\lambda }{4} - \frac{\lambda }{6} = \frac{\lambda }{{12}}\)

Biên độ dao động tại điểm M là: \({A_M} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{\frac{\lambda }{{12}}}}{\lambda }} \right| = \left| {{A_{\rm{0}}}\sin \frac{\pi }{6}} \right| = \frac{{{A_{\rm{0}}}}}{2} = 4cm\)

Cứ sau những khoảng thời gian liên tiếp \(\frac{T}{2}\) thì sợi dây duỗi thẳng.

Ta có: \(\frac{T}{2} = {\rm{0}},25 \Rightarrow T = {\rm{0}},5 \Rightarrow \omega  = \frac{{2\pi }}{T} = 4\pi \)

Tốc độ dao động cực đại của điểm M là: \({v_{M\max }} = {A_M}.\omega  = 4.4\pi  = 16\pi cm/s\)

Đáp án C.

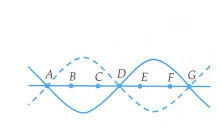
Các điểm B, C, E, F dao động cùng biên độ b sẽ cách nút gần nó nhất những khoảng bằng nhau:

AB = CD = DE = FG

Mặt khác, các điểm B, C, E, F cách đều nhau khoảng lm nên ta có

BC = CE = EF = 1m

Từ hình vẽ, ta có: \(\left\{ \begin{array}{l}CE = CD + DE\\CD = DE\end{array} \right. \Rightarrow CE = 2CD \Rightarrow BC = 2CD \Rightarrow BC = AB + CD\)

Mặt khác \(AB + BC + CD = \frac{\lambda }{2} \Rightarrow 2BC = \frac{\lambda }{2} \Rightarrow \lambda  = 2.2.1 = 4m \Rightarrow \lambda f = 4.5{\rm{0}} = 2{\rm{00}}\)

Biên độ là \(b = 2a\left| {\sin \frac{{2\pi AB}}{\lambda }} \right| = 2a\left| {\sin \frac{{2\pi \frac{{AD}}{4}}}{\lambda }} \right| = 2a\left| {\sin \frac{{2\pi \frac{\lambda }{8}}}{\lambda }} \right| = a\sqrt 2 \)

Đáp án A.

Xét điểm C cách A với CA = d. Biên độ của sóng dừng tại C: \({A_c} = 2a\left| {\sin \frac{{2\pi d}}{\lambda }} \right|\)

Để a _c = a (bằng nửa biên độ của B là bụng sóng):

\({A_c} = a \Leftrightarrow a = 2a\left| {\sin \frac{{2\pi d}}{\lambda }} \right| \Leftrightarrow \left| {\sin \frac{{2\pi d}}{\lambda }} \right| = \frac{1}{2} \Rightarrow \frac{{2\pi d}}{\lambda } = \frac{\pi }{6} + k2\pi \)

\( \Rightarrow d = \left( {\frac{1}{{12}} + k} \right)\lambda \) với \(\lambda  = 4AB = 56cm\)

Điểm C gần A nhất ứng với \(k = {\rm{0}} \Rightarrow AV = \frac{\lambda }{{12}} = \frac{{56}}{{12}} = \frac{{14}}{3}\left( {cm} \right)\)

Đáp án A.

Bề rộng của bụng là 4a thì biên độ của một điểm trên dây khi có sóng dừng

\(A = 2a\left| {\cos \frac{{2\pi d}}{\lambda }} \right|\)

Trong đó d là khoảng cách từ một điểm trên dây đến điểm bụng gần nó nhất.

Các điểm có cùng biên độ và cùng pha sẽ đối xứng với nhau qua điểm bụng. Mà khoảng cách gần nhất giữa hai điểm dao động cùng pha cùng biên độ a là 20 cm nên khoảng cách từ một điểm đến bụng là 10 cm. Do đó ta có

\(a = 2a\left| {{\rm{cos}}\frac{{2\pi .1{\rm{0}}}}{\lambda }} \right| \Leftrightarrow \left| {\cos \frac{{2\pi .1{\rm{0}}}}{\lambda }} \right| = \frac{1}{2} \Rightarrow \frac{{2\pi .1{\rm{0}}}}{\lambda } = \frac{\pi }{3} \Rightarrow \lambda  = 6{\rm{0}}cm.\)

Vì hai đầu cố định nên \(l = k\frac{\lambda }{2} \Rightarrow k = 4\). Vậy có 4 bụng trên AB

Đáp án B.

Vì 1 chu kì dòng điện đổi chiều 2 lần nên nam châm hút dây 2 lần, do đó tần số sóng dừng trên dây là \(f' = 2f = 1{\rm{00}}Hz\)

Ta có \(f' = \frac{{kv}}{{2l}} = \frac{v}{l}\)  (do có 2 bụng sóng) nên suy ra v = 100.1,2 = 120 m/s.

Đáp án A.

Khi có sóng dừng, số bó sóng trên dây: \(\frac{{2l}}{\lambda } = \frac{{2.3{\rm{0}}}}{{2{\rm{0}}}} = 3\left( {bo\`u } \right)\)

Trên mỗi bó có 2 điểm dao động với biên độ 6mm. Suy ra số điểm trên dây mà phần tử tại đó dao động với biên độ 6 mm là 2.3 = 6 điểm