Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1 — Không quảng cáo

Với a là số thực dương và m, n là hai số thực tùy ý thì ${\left( {{a^m}} \right)^n} = {a^{m.n}}$.

Với a là số thực dương và m, n là hai số thực tùy ý thì ${\left( {{a^m}} \right)^n} = {a^{m.n}}$.

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì ${a^{ - n}} = \frac{1}{{{a^n}}}$.

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì ${a^{ - n}} = \frac{1}{{{a^n}}}$.

$\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}$ (với các biểu thức đều có nghĩa).

Ta có: $\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}$.

${a^m}.{a^n} = {a^{m + n}};{\left( {{a^m}} \right)^n} = {a^{mn}},{a^m}:{a^n} = {a^{m - n}}$ (a khác 0).

$P = \frac{{{a^{\sqrt 5  + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}} = \frac{{{a^{\sqrt 5  + 1 + 7 - \sqrt 5 }}}}{{{a^{\left( {3 + \sqrt 2 } \right)\left( {3 - \sqrt 2 } \right)}}}} = \frac{{{a^8}}}{{{a^7}}} = a$

Nếu $a > 1$ thì ${a^\alpha } > {a^\beta } \Leftrightarrow \alpha  > \beta$

Nếu $0 < a < 1$ thì ${a^\alpha } > {a^\beta } \Leftrightarrow \alpha  < \beta$

Ta có: $\frac{1}{{{a^{ - 3}}}} = {a^3} = {a^{\sqrt 9 }}$ nên ${a^{\sqrt 8 }} < {a^{\sqrt 9 }}$

Vì $\sqrt 8  < \sqrt 9$, mà ${a^{\sqrt 8 }} < {a^{\sqrt 9 }}$ nên $a > 1$. Do đó, $a = \frac{3}{2}$ thỏa mãn yêu cầu bài toán.

${\log _a}b$ xác định khi và chỉ khi $a > 0,a \ne 1,b > 0$.

${\log _a}b$ xác định khi và chỉ khi $a > 0,a \ne 1,b > 0$.

Với a, b là số thực dương và $a \ne 1$ thì ${\log _a}{a^b} = b$.

${\log _{1000}}{1000^3} = 3$

Lôgarit cơ số 10 của số thực dương b được gọi là lôgarit thập phân của b và kí hiệu logb hay lg b.

Lôgarit cơ số e của số thực dương b được gọi là lôgarit tự nhiên của b và kí hiệu ln b.

Lôgarit cơ số 10 của số thực dương a kí hiệu là $\log a$.

Với a, b là số thực dương và $a \ne 1$ thì ${a^{{{\log }_a}b}} = b,{\log _{{a^\alpha }}}b = \frac{1}{\alpha }{\log _a}b;{\log _a}{b^\alpha } = \alpha {\log _a}b$.

${4^{{{\log }_{\sqrt 2 }}3}} = {2^{2{{\log }_{{2^{\frac{1}{2}}}}}3}} = {2^{4{{\log }_2}3}} = {2^{{{\log }_2}{3^4}}} = 81$

Với a, b là số thực dương và $a \ne 1$ thì ${\log _a}{b^\alpha } = \alpha {\log _a}b,\log {\,_a}a = 1$

Với a là số thực dương, $a \ne 1$, $M > 0,N > 0$ thì ${\log _a}\frac{M}{N} = {\log _a}M - {\log _a}N$.

${\log _5}15 - 2{\log _5}\sqrt 3  = {\log _5}15 - {\log _5}3 = {\log _5}\frac{{15}}{3} = {\log _5}5 = 1$

Đồ thị hàm số hàm số $y = {a^x}\left( {a > 0,a \ne 1} \right)$ cắt trục tung tại điểm có tung độ bằng 1.

Đồ thị hàm số hàm số $y = {a^x}\left( {a > 0,a \ne 1} \right)$ cắt trục tung tại điểm có tung độ bằng 1.

Hàm số $y = {a^x}\left( {a > 0,a \ne 1} \right)$ có tập xác định là $D = \left( { - \infty ; + \infty } \right)$.

Hàm số $y = {a^x}\left( {a > 0,a \ne 1} \right)$ có tập xác định là $D = \left( { - \infty ; + \infty } \right)$.

Nếu $a > 1$ thì hàm số $y = {\log _2}x$ đồng biến trên $\left( {0; + \infty } \right)$.

Vì $2 > 1$ nên hàm số $y = {\log _2}x$ đồng biến trên $\left( {0; + \infty } \right)$. Do đó, hàm số $y = {\log _2}x$ đồng biến trên $\left( {1; + \infty } \right)$

Hàm số $y = {a^x}\left( {a > 0,a \ne 1} \right)$ được gọi là hàm số mũ cơ số a.

Hàm số $y = {\left( {\frac{\pi }{2}} \right)^x}$ được gọi là hàm số mũ.

Xét xem đồ thị hàm số nào đi qua điểm $\left( { - 1;3} \right)$ và (0;1) thì đó là đồ thị hàm số cần tìm.

Ta thấy đồ thị hàm số $y = {\left( {\frac{1}{3}} \right)^x}$ đi qua điểm $\left( { - 1;3} \right)$ và (0;1) nên hàm số $y = {\left( {\frac{1}{3}} \right)^x}$ là hàm số cần tìm.

Cho hàm số $y = {a^x}\left( {a > 0,a \ne 1} \right)$:

+ Nếu $a > 1$ thì hàm số đồng biến trên $\mathbb{R}$.

+ Nếu $0 < a < 1$ thì hàm số nghịch biến trên $\mathbb{R}$.

Vì $2 > 1$ nên hàm số $f\left( x \right) = {2^x}$ đồng biến trên $\mathbb{R}$.

Do đó, $\mathop {\max }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right) = {2^3} = 8;\mathop {\min }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( { - 2} \right) = {2^{ - 2}} = \frac{1}{4}$

Suy ra: $M = 8,m = \frac{1}{4} \Rightarrow Mm = 8.\frac{1}{4} = 2$.

Cho phương trình ${a^x} = b\left( {a > 0,a \ne 1} \right)$:

+ Nếu $b \le 0$ thì phương trình vô nghiệm.

+ Nếu $b > 0$ thì phương trình có nghiệm duy nhất $x = {\log _a}b$.

${2^x} = 9 \Leftrightarrow x = {\log _2}9$

Vậy phương trình có nghiệm là $x = {\log _2}9$.

${a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)$

${2^{2x - 1}} = {2^x} \Leftrightarrow 2x - 1 = x \Leftrightarrow x = 1$

Vậy phương trình đã cho có nghiệm $x = 1$

${a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)$

${\pi ^{x - 3}} = \frac{1}{\pi } \Leftrightarrow {\pi ^{x - 3}} = {\pi ^{ - 1}} \Leftrightarrow x - 3 =  - 1 \Leftrightarrow x = 2$

Vậy phương trình có nghiệm $x = 2$.

${a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)$

${\left( {\frac{1}{{16}}} \right)^{x + 1}} = {64^{2x}} \Leftrightarrow {4^{ - 2\left( {x + 1} \right)}} = {4^{3.2x}} \Leftrightarrow  - 2x - 2 = 6x \Leftrightarrow 8x =  - 2 \Leftrightarrow x = \frac{{ - 1}}{4}$

Nếu $0 < a < 1$ thì ${\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) \le v\left( x \right)\end{array} \right.$.

${\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge 1 \Leftrightarrow {\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge {\log _{\frac{2}{3}}}\frac{2}{3} \Leftrightarrow \left\{ \begin{array}{l}x - 3 > 0\\x - 3 \le \frac{2}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 3\\x \le \frac{{11}}{3}\end{array} \right.$

Do đó, tập nghiệm của bất phương trình là: $S = \left( {3;\frac{{11}}{3}} \right]$.

Với $a > 0,a \ne 1$ thì ${\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.$ (có thể thay $u\left( x \right) > 0$ bằng $v\left( x \right) > 0$)

Điều kiện: $x > 0$

${\log _3}x + {\log _3}\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right) \Leftrightarrow {\log _3}x\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right)$

$\Leftrightarrow {x^2} + x = 5x + 12 \Leftrightarrow {x^2} - 4x - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 2\left( L \right)\\x = 6\left( {TM} \right)\end{array} \right.$

Vậy phương trình đã cho có một nghiệm là $x = 6$

Với $a > 1$ thì ${a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) > v\left( x \right)$

${\left( {\frac{1}{{\sqrt 5 }}} \right)^{2x}} < {25^{1 - x}} \Leftrightarrow {5^{\frac{{ - 2x}}{2}}} < {5^{2\left( {1 - x} \right)}} \Leftrightarrow  - x < 2 - 2x\left( {do\;5 > 1} \right) \Leftrightarrow x < 2$

Vậy tập nghiệm của bất phương trình đã cho là: $S = \left( { - \infty ;2} \right)$.

Góc giữa hai đường thẳng có số đo không vượt quá 90 ⁰ .

Vì góc giữa hai đường thẳng có số đo không vượt quá 90 ⁰ nên góc giữa hai đường thẳng có thể bằng 90 ⁰ .

Hai đường thẳng vuông góc với nhau nếu góc giữa chúng bằng ${90^0}$.

Trong không gian cho hai đường thẳng a và b vuông góc với nhau thì góc giữa chúng bằng ${90^0}$.

+ Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu $\left( {a,b} \right)$ hoặc $\widehat {\left( {a;b} \right)}$.

+ Góc giữa hai đường thẳng không vượt quá ${90^0}$.

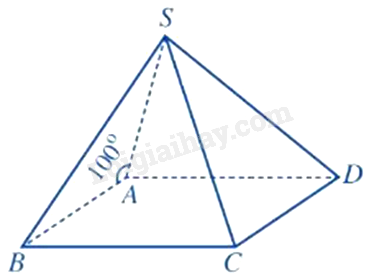
Vì ABCD là hình bình hành nên $AB//CD$

Do đó, $\left( {SA,CD} \right) = \left( {SA,AB} \right) = {180^0} - \widehat {SAB} = {80^0}$

Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.

Vì M, N lần lượt là trung điểm của các cạnh SB và SD nên MN là đường trung bình của tam giác SBD, do đó, MN//BD.

Vì ABCD là hình thoi nên $AC \bot BD$

Vì $AC \bot BD$, MN//BD nên $AC \bot MN \Rightarrow \left( {AC,MN} \right) = {90^0}$.

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Có duy nhất một đường thẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Vì đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P nên $d \bot d' \Rightarrow \left( {d,d'} \right) = {90^0}$

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

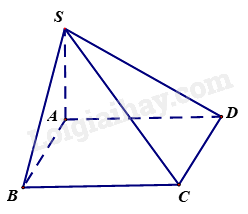
Vì $SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC$

Mà ABCD là hình chữ nhật nên $BC \bot AB$

Ta có: $SA \bot BC,BC \bot AB,$ AB và SA cắt nhau tại A và nằm trong mặt phẳng (SAB).

Do đó, $BC \bot \left( {SAB} \right)$

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

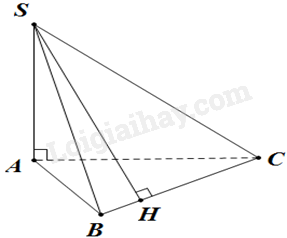
Vì $SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC$, mà $BC \bot SH$ và SA và SH cắt nhau tại S và nằm trong mặt phẳng (SAH) nên $BC \bot \left( {SAH} \right)$.

Lại có: $AH \subset \left( {SAH} \right)$ nên $BC \bot AH$.

Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

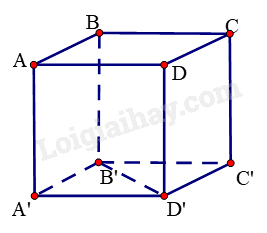
Vì ABCD.A’B’C’D’ là hình lập phương nên $AA' \bot \left( {A'B'C'D'} \right)$, mà $B'D' \subset \left( {A'B'C'D'} \right)$ nên $AA' \bot B'D'$. Do đó, góc giữa hai đường thẳng A’A và D’B’ bằng ${90^0}$.

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

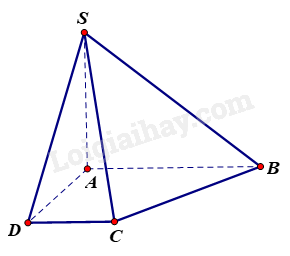
Vì $SA \bot \left( {ABCD} \right),AB \subset \left( {ABCD} \right) \Rightarrow SA \bot AB$.

Vì ABCD là hình thang vuông tại A nên $AB \bot AD$.

Ta có: $AB \bot AD$, $SA \bot AB$ và SA và AD cắt nhau tại A và nằm trong mặt phẳng (SAD)

Do đó, $AB \bot \left( {SAD} \right) \Rightarrow AB \bot SD$. Suy ra, $\left( {AB,SD} \right) = {90^0}$.

+ Hàm số có dạng $y = \frac{1}{{\sqrt {u\left( x \right)} }}$ xác định khi $u\left( x \right) > 0$.

+ Hàm $y = {\log _a}u\left( x \right)\left( {a > 0,a \ne 1} \right)$ xác định khi $u\left( x \right) > 0$.

a) Với $m = \frac{1}{3}$ ta có: $y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 1} \right)} }}$.

Hàm số $y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 1} \right)} }}$ xác định khi ${\log _3}\left( {{x^2} - 2x + 1} \right) > 0 \Leftrightarrow {x^2} - 2x + 1 > 1 \Leftrightarrow {x^2} - 2x > 0 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < 0\end{array} \right.$

Vậy với $m = \frac{1}{3}$ thì tập xác định của hàm số là: $D = \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)$.

b) Hàm số $y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}$ có tập xác định là $\mathbb{R}$ khi và chỉ khi ${\log _3}\left( {{x^2} - 2x + 3m} \right) > 0$ với mọi $x \in \mathbb{R}$

$\Leftrightarrow {x^2} - 2x + 3m > 1$ với mọi $x \in \mathbb{R}$

$\Leftrightarrow {x^2} - 2x + 3m - 1 > 0$ với mọi $x \in \mathbb{R}$

$\Leftrightarrow \left\{ \begin{array}{l}1 > 0\\\Delta ' < 0\end{array} \right. \Leftrightarrow {\left( { - 1} \right)^2} - 3m + 1 < 0 \Leftrightarrow m > \frac{2}{3}$

Vậy với $m > \frac{2}{3}$ thì hàm số $y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}$ có tập xác định là $\mathbb{R}$.

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

a) Vì $SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \Rightarrow SA \bot DC$

Vì ABCD là hình vuông nên $DC \bot AD$.

Mà SA và AD cắt nhau tại A và nằm trong mặt phẳng (SAD). Do đó, $DC \bot \left( {SAD} \right)$

Lại có: $AK \subset \left( {SAD} \right) \Rightarrow DC \bot AK$. Mặt khác, $AK \bot SD \Rightarrow AK \bot \left( {SDC} \right) \Rightarrow AK \bot SC$

Vì $SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC$

Vì ABCD là hình vuông nên $BC \bot AB$.

Mà SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB). Do đó, $BC \bot \left( {SAB} \right)$

Lại có: $AH \subset \left( {SAB} \right) \Rightarrow BC \bot AH$. Mặt khác, $AH \bot SB \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC$

Ta có: $AK \bot SC$, $AH \bot SC$ và AK và AH cắt nhau tại A nằm trong mặt phẳng (AHK) nên $SC \bot \left( {AHK} \right)$.

b) Ta có: $SA \bot \left( {ABCD} \right) \Rightarrow \left\{ \begin{array}{l}SA \bot AB\\SA \bot AD\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat {SAB} = {90^0}\\\widehat {SAD} = {90^0}\end{array} \right.$

Tam giác SAB và tam giác SAD có: SA là cạnh chung, $\widehat {SAB} = \widehat {SAD} = {90^0}$, $AB = AD$.

Do đó, $\Delta SAB = \Delta SAD\left( {c.g.c} \right) \Rightarrow SB = SD$, $SH = SK$.

Suy ra: $\frac{{SH}}{{SB}} = \frac{{SK}}{{SD}}$. Do đó, HK//BD (1)

Vì ABCD là hình vuông nên $AC \bot BD$.

Vì $SA \bot \left( {ABCD} \right),DB \subset \left( {ABCD} \right) \Rightarrow SA \bot DB$

Mà SA và AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên $DB \bot \left( {SAC} \right)$ (2)

Từ (1) và (2) ta có: $HK \bot \left( {SAC} \right)$. Mà $AI \subset \left( {SAC} \right)$, suy ra $HK \bot AI$.

Nếu $a > 1$ thì ${\log _a}u\left( x \right) < {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) < v\left( x \right)\end{array} \right.$.

TXĐ: $D = \left( { - \infty ; - 4} \right) \cup \left( {4; + \infty } \right)$.

Ta có: ${\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{\left( {x - 4} \right)\left( {x + 4} \right)}}{{27}}$

$\begin{array}{l} \Leftrightarrow {\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{{x^2} - 16}}{{27}}\\ \Leftrightarrow {\rm{lo}}{{\rm{g}}_3}7.\left[ {{\rm{lo}}{{\rm{g}}_7}\left( {{x^2} - 16} \right) - 3} \right] < {\rm{lo}}{{\rm{g}}_7}\left( {{x^2} - 16} \right) - 3{\rm{lo}}{{\rm{g}}_7}3\\ \Leftrightarrow \left( {{\rm{lo}}{{\rm{g}}_3}7 - 1} \right){\rm{.lo}}{{\rm{g}}_7}\left( {{x^2} - 16} \right) < 3{\rm{lo}}{{\rm{g}}_3}7 - 3{\rm{lo}}{{\rm{g}}_7}3\\ \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < \frac{{3\left( {{{\log }_3}7 - {{\log }_7}3} \right)}}{{{{\log }_3}7 - 1}}\end{array}$

$\Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < \frac{{3\left( {{{\log }_3}7 - \frac{1}{{{{\log }_3}7}}} \right)}}{{{{\log }_3}7 - 1}}$$\Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < \frac{{3\left( {{{\log }_3}7 + 1} \right)}}{{{{\log }_3}7}}$

$\begin{array}{l} \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < 3\left( {1 + {{\log }_7}3} \right)\\ \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < {\log _7}{21^3}\end{array}$

$\Leftrightarrow {x^2} - 16 < {21^3} \Leftrightarrow  - \sqrt {9277}  < x < \sqrt {9277}$

Kết hợp với điều kiện xác định ta có: $\left[ \begin{array}{l} - \sqrt {9277}  < x <  - 4\\4 < x < \sqrt {9277} \end{array} \right.$

Vì x là số tự nhiên nên $x \in \left\{ {5;6;7;...;96} \right\}$.