Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 5
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng (với giả thiết các biểu thức đều có nghĩa).
Đề bài
Chọn đáp án đúng (với giả thiết các biểu thức đều có nghĩa).
-
A.
\(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\) .
-
B.
\(\tan \left( {a + b} \right) = \frac{{\tan a - \tan b}}{{1 - \tan a\tan b}}\).
-
C.
\(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 + \tan a\tan b}}\).
-
D.
\(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{\tan a\tan b - 1}}\).
Chọn câu đúng
-
A.
Hàm số \(y = \cot x\) là hàm số lẻ và tuần hoàn với chu kì 2\(\pi \) .
-
B.
Hàm số \(y = \cot x\) là hàm số lẻ và tuần hoàn với chu kì \(\pi \).
-
C.
Hàm số \(y = \cot x\) là hàm số chẵn và tuần hoàn với chu kì 2\(\pi \).
-
D.
Hàm số \(y = \cot x\) là hàm số chẵn và tuần hoàn với chu kì \(\pi \).
Khi biểu diễn trên đường tròn lượng giác, góc lượng giác nào trong các góc lượng giác dưới đây có cùng điểm cuối, cùng điểm đầu với góc lượng giác có số đo \(\frac{\pi }{4}\).
-
A.
\(\frac{\pi }{4} + k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)\) .
-
B.
\(\frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\).
-
C.
\(\frac{\pi }{4} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
-
D.
\(\frac{\pi }{4} + k3\pi \left( {k \in \mathbb{Z}} \right)\).
Nếu \(\sin \alpha > 0,\cos \alpha < 0\) thì \(\alpha \) thuộc góc phần tư nào?
-
A.
(I).
-
B.
(II).
-
C.
(III).
-
D.
(IV).
Chọn đáp án đúng:
-
A.
\(\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \left( {k \in \mathbb{Z}} \right)\).
-
B.
\(\sin \left( {\alpha + k2\pi } \right) = - \sin \alpha \left( {k \in \mathbb{Z}} \right)\).
-
C.
\(\sin \left( {\alpha + k2\pi } \right) = \cos \alpha \left( {k \in \mathbb{Z}} \right)\).
-
D.
\(\sin \left( {\alpha + k2\pi } \right) = - \cos \alpha \left( {k \in \mathbb{Z}} \right)\).
Cấp số cộng \(\left( {{u_n}} \right)\) với công sai d được cho bởi hệ thức:
-
A.
\({u_n} = {u_{n - 1}} + 2d\) với \(n \ge 2\).
-
B.
\({u_n} = 2{u_{n + 1}}.d\) với \(n \ge 2\).
-
C.
\({u_n} = {u_{n - 1}}.d\) với \(n \ge 2\).
-
D.
\({u_n} = {u_{n - 1}} + d\) với \(n \ge 2\).
Dãy số \(\left( {{u_n}} \right)\) gồm các số khác 0 thỏa mãn tỉ số \(\frac{{{u_n}}}{{{u_{n - 1}}}}\) không đổi thì dãy số \(\left( {{u_n}} \right)\) là:
-
A.
Cấp số cộng.
-
B.
Cấp số nhân.
-
C.
Cả A và B đều đúng.
-
D.
Cả A và B đều sai.
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {2020^n}\). Tính \({u_{n + 1}}\).
-
A.
\({u_{n + 1}} = {2020^n} + 2020\).
-
B.
\({u_{n + 1}} = {2020^{n + 1}}\).
-
C.
\({u_{n + 1}} = {2020^n} + 1\).
-
D.
\({u_{n + 1}} = 2020\left( {n + 1} \right)\).
\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) khi và chỉ khi:
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\) .
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + a} \right) = 0\) .
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}.a} \right) = 0\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 1\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Mệnh đề nào đúng?
-
A.
Nếu \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) không có nghiệm trong \(\left( {a;b} \right)\).
-
B.
Nếu \(f\left( a \right).f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm trong \(\left( {a;b} \right)\).
-
C.
Nếu \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm trong \(\left( {a;b} \right)\).
-
D.
Cả A, B, C đều sai.
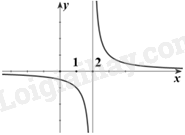
-
A.
\(x = 2\).
-
B.
\(x = 1\).
-
C.
\(x = 0\)
-
D.
\(x = - 1\).
Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = - \infty \) thì:
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = - \infty \) .
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = + \infty \).
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = 0\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = a\).
Cho hình chóp S. ABCD có O là giao điểm của AC và BD. Gọi M, I lần lượt là trung điểm của BD, SD. Điểm nào dưới đây thuộc mặt phẳng (SOC)?
-
A.
Điểm A .
-
B.
Điểm B.
-
C.
Điểm I.
-
D.
Điểm M.
Chọn đáp án sai .
-
A.
Trong không gian, có ba đường thẳng phân biệt cùng đi qua hai điểm phân biệt cho trước.
-
B.
Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
-
C.
Có duy nhất một mặt phẳng đi qua ba điểm không thẳng hàng.
-
D.
Nếu một đường thẳng đi qua hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Với điều kiện nào dưới đây thì đường thẳng d song song với mặt phẳng (P)?
-
A.
a//d, \(a \subset \left( P \right)\) .
-
B.
d//a, a//(P).
-
C.
\(d \cap \left( P \right) = \emptyset \).
-
D.
d//a, \(a \cap \left( P \right) = \emptyset \).
Nếu đường thẳng d và mặt phẳng (P) có … điểm chung thì d cắt mặt phẳng (P).
Từ (cụm từ) thích hợp điền vào “…” để được câu đúng là:
-
A.
duy nhất một.
-
B.
hai.
-
C.
không.
-
D.
vô số.
Hình chóp S. ABCD có bao nhiêu đỉnh?
-
A.
7 .
-
B.
5.
-
C.
6.
-
D.
8.
Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa a và cắt mặt phẳng (P) theo giao tuyến b. Kết luận nào sau đây đúng?
-
A.
a và b cắt nhau .
-
B.
a và b trùng nhau .
-
C.
a và b chéo nhau.
-
D.
a và b song song.
Cho \(\tan \alpha = -2\) và \(\frac{\pi }{2} < \alpha < \pi \). Chọn đáp án đúng.
-
A.
\(\cos \alpha = - \sqrt 5 \) .
-
B.
\(\cos \alpha = \frac{{\sqrt 5 }}{5}\).
-
C.
\(\cos \alpha = \frac{{ - \sqrt 5 }}{5}\).
-
D.
\(\cos \alpha = \sqrt 5 \).
Rút gọn biểu thức \(A = \frac{{\sin x + \sin 2x + \sin 3x}}{{\cos x + \cos 2x + \cos 3x}}\)
-
A.
\(A = \cot 2x\) .
-
B.
\(A = \tan 2x\).
-
C.
\(A = \sin 2x\).
-
D.
\(A = \cos 2x\).
Giá trị của biểu thức \(\sin \frac{{37\pi }}{{12}}\) bằng:
-
A.
\(\frac{{\sqrt 6 - \sqrt 2 }}{4}\) .
-
B.
\( - \frac{{\sqrt 6 + \sqrt 2 }}{4}\).
-
C.
\(\frac{{\sqrt 6 + \sqrt 2 }}{4}\).
-
D.
\(\frac{{ - \sqrt 6 + \sqrt 2 }}{4}\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2024\) và \({u_n} = {u_{n - 1}} - 3\) với \(n \ge 2\), \(n \in \mathbb{N}*\). Số hạng tổng quát của cấp số cộng đã cho là:
-
A.
\({u_n} = - 3n - 2027\) với \(n \ge 2\), \(n \in \mathbb{N}*\) .
-
B.
\({u_n} = - 3n + 2027\) với \(n \ge 2\), \(n \in \mathbb{N}*\).
-
C.
\({u_n} = 3n + 2027\) với \(n \ge 2\), \(n \in \mathbb{N}*\).
-
D.
\({u_n} = 3n + 2027\) với \(n \ge 2\), \(n \in \mathbb{N}*\).
Theo ước tính, kể từ lúc mới mua, cứ sau mỗi 200 lần sạc thì pin của điện thoại X sẽ giảm 4% so với chu kỳ 200 lần sạc trước đó. Hỏi sau 1 200 lần sạc thì pin của điện thoại X còn lại bao nhiêu phần trăm so với lúc mới mua? (làm tròn đến chữ số thập phân thứ hai)
-
A.
78,28% .
-
B.
78,27% .
-
C.
81,54% .
-
D.
81,53% .
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 25{n^2} + 10n + 9\). Chọn khẳng định đúng:
-
A.
Dãy số trên bị chặn dưới .
-
B.
Dãy số trên bị chặn trên.
-
C.
Dãy số trên không bị chặn.
-
D.
Dãy số trên bị chặn.
Tìm số thực a khác 0 sao cho \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{n^2} - 2}}{{a{n^2} - 1}} = 2\)
-
A.
\(a = - \frac{1}{2}\) .
-
B.
\(a = - 2\).
-
C.
\(a = 2\).
-
D.
\(a = \frac{1}{2}\).
Giới hạn \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} - 18n} - n} \right)\) bằng:
-
A.
9 .
-
B.
\( - 9\).
-
C.
18.
-
D.
\( + \infty \).
Biểu diễn số thập phân vô hạn tuần hoàn 3,333… dưới dạng phân số ta được:
-
A.
\(\frac{{10}}{3}\) .
-
B.
\(\frac{3}{{10}}\).
-
C.
\(\frac{{100}}{3}\).
-
D.
\(\frac{{100}}{{33}}\).
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của BC, I là giao điểm của AM và BD, \(\left( \alpha \right)\) là mặt phẳng qua A, M và song song với SD. Mặt phẳng \(\left( \alpha \right)\) cắt SB tại N. Tỉ số \(\frac{{SN}}{{SB}}\) là:
-
A.
\(\frac{3}{4}\) .
-
B.
\(\frac{1}{2}\).
-
C.
\(\frac{2}{3}\).
-
D.
\(\frac{1}{3}\).
Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD, P là điểm thuộc SA. Giao tuyến của hai mặt phẳng (SAD) và (PMN) là đường thẳng:
-
A.
Qua P song song với AB .
-
B.
Qua P song song với AD.
-
C.
PD.
-
D.
Qua P song song với MC.
Cho tứ diện ABCD và điểm M thuộc miền trong tam giác ACD. Gọi I và J lần lượt là hai điểm trên cạnh BC và BD sao cho IJ sao cho IJ không song song với CD. Gọi H là giao điểm của IJ với CD, K là giao điểm của MH và AC. Giao tuyến của hai mặt phẳng (ACD) và (IJM) là:
-
A.
KI .
-
B.
KJ.
-
C.
HI.
-
D.
HM.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, SD. Mặt phẳng (OMN) song song với mặt phẳng nào dưới đây?
-
A.
(SCD).
-
B.
(SBC).
-
C.
(ABCD).
-
D.
(SAB).
Trong mẫu số liệu ghép nhóm, tứ phân vị thứ ba \({Q_3}\) thể hiện:
-
A.
Có 25% số giá trị nhỏ hơn \({Q_3}\) .
-
B.
Có 75% số giá trị nhỏ hơn \({Q_3}\).
-
C.
Có 25% số giá trị lớn hơn \({Q_3}\).
-
D.
Có 75% số giá trị lớn hơn \({Q_3}\).
Trong mẫu số liệu ghép nhóm, độ dài của nhóm \(\left[ {12;15} \right)\) bằng bao nhiêu?
-
A.
12 .
-
B.
15.
-
C.
3.
-
D.
27.
Cho mẫu số liệu ghép nhóm về thống kê nhiệt độ tại một địa điểm trong 30 ngày như dưới đây:

Nhiệt độ trung bình trong 30 ngày là:
-
A.
22,8\(^oC\) .
-
B.
23\(^oC\).
-
C.
23,2\(^oC\).
-
D.
23,4\(^oC\).
Mẫu số liệu ghép nhóm dưới đây thống kê doanh thu cửa hàng (triệu) trong tháng như sau:

Mốt của mẫu số liệu này là (làm tròn đến chữ số thập phân thứ nhất):
-
A.
9,2 triệu .
-
B.
9,1 triệu.
-
C.
9,3 triệu.
-
D.
9,4 triệu.
Lời giải và đáp án
Chọn đáp án đúng (với giả thiết các biểu thức đều có nghĩa).
-
A.
\(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\) .
-
B.
\(\tan \left( {a + b} \right) = \frac{{\tan a - \tan b}}{{1 - \tan a\tan b}}\).
-
C.
\(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 + \tan a\tan b}}\).
-
D.
\(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{\tan a\tan b - 1}}\).
Đáp án : A
Sử dụng công thức: \(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\).
Ta có: \(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\)
Chọn câu đúng
-
A.
Hàm số \(y = \cot x\) là hàm số lẻ và tuần hoàn với chu kì 2\(\pi \) .
-
B.
Hàm số \(y = \cot x\) là hàm số lẻ và tuần hoàn với chu kì \(\pi \).
-
C.
Hàm số \(y = \cot x\) là hàm số chẵn và tuần hoàn với chu kì 2\(\pi \).
-
D.
Hàm số \(y = \cot x\) là hàm số chẵn và tuần hoàn với chu kì \(\pi \).
Đáp án : B
Sử dụng kiến thức về hàm số \(y = \cot x\): Hàm số \(y = \cot x\) là hàm số lẻ và tuần hoàn với chu kì \(\pi \).
Hàm số \(y = \cot x\) là hàm số lẻ và tuần hoàn với chu kì \(\pi \).
Khi biểu diễn trên đường tròn lượng giác, góc lượng giác nào trong các góc lượng giác dưới đây có cùng điểm cuối, cùng điểm đầu với góc lượng giác có số đo \(\frac{\pi }{4}\).
-
A.
\(\frac{\pi }{4} + k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)\) .
-
B.
\(\frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\).
-
C.
\(\frac{\pi }{4} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
-
D.
\(\frac{\pi }{4} + k3\pi \left( {k \in \mathbb{Z}} \right)\).
Đáp án : C
Sử dụng kiến thức: Cho hai góc lượng giác (Ou, Ov), (O’u’, O’v’) có tia đầu trùng nhau, tia cuối cùng nhau nếu: \(\left( Ou,Ov \right)=\left( O’u’,O’v’ \right)+k2\pi \) với k là số nguyên.
Góc lượng giác có cùng điểm cuối, cùng điểm đầu với góc lượng giác có số đo \(\frac{\pi }{4}\) là: \(\frac{\pi }{4} + k2\pi \left( {k \in \mathbb{Z}} \right)\)
Nếu \(\sin \alpha > 0,\cos \alpha < 0\) thì \(\alpha \) thuộc góc phần tư nào?
-
A.
(I).
-
B.
(II).
-
C.
(III).
-
D.
(IV).
Đáp án : B
Sử dụng kiến thức về dấu của giá trị lượng giác: Nếu \(\sin \alpha > 0,\cos \alpha < 0\) thì \(\alpha \) thuộc góc phần tư thứ (II).
Nếu \(\sin \alpha > 0,\cos \alpha < 0\) thì \(\alpha \) thuộc góc phần tư thứ (II).
Chọn đáp án đúng:
-
A.
\(\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \left( {k \in \mathbb{Z}} \right)\).
-
B.
\(\sin \left( {\alpha + k2\pi } \right) = - \sin \alpha \left( {k \in \mathbb{Z}} \right)\).
-
C.
\(\sin \left( {\alpha + k2\pi } \right) = \cos \alpha \left( {k \in \mathbb{Z}} \right)\).
-
D.
\(\sin \left( {\alpha + k2\pi } \right) = - \cos \alpha \left( {k \in \mathbb{Z}} \right)\).
Đáp án : A
Sử kiến thức giá trị lượng giác của góc lượng giác: \(\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \left( {k \in \mathbb{Z}} \right)\)
\(\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \left( {k \in \mathbb{Z}} \right)\)
Cấp số cộng \(\left( {{u_n}} \right)\) với công sai d được cho bởi hệ thức:
-
A.
\({u_n} = {u_{n - 1}} + 2d\) với \(n \ge 2\).
-
B.
\({u_n} = 2{u_{n + 1}}.d\) với \(n \ge 2\).
-
C.
\({u_n} = {u_{n - 1}}.d\) với \(n \ge 2\).
-
D.
\({u_n} = {u_{n - 1}} + d\) với \(n \ge 2\).
Đáp án : D
Sử dụng kiến thức về cấp số cộng: Cấp số cộng \(\left( {{u_n}} \right)\) với công sai d được cho bởi hệ thức truy hồi \({u_n} = {u_{n - 1}} + d\) với \(n \ge 2\).
Cấp số cộng \(\left( {{u_n}} \right)\) với công sai d được cho bởi hệ thức truy hồi \({u_n} = {u_{n - 1}} + d\) với \(n \ge 2\).
Dãy số \(\left( {{u_n}} \right)\) gồm các số khác 0 thỏa mãn tỉ số \(\frac{{{u_n}}}{{{u_{n - 1}}}}\) không đổi thì dãy số \(\left( {{u_n}} \right)\) là:
-
A.
Cấp số cộng.
-
B.
Cấp số nhân.
-
C.
Cả A và B đều đúng.
-
D.
Cả A và B đều sai.
Đáp án : B
Sử dụng kiến thức về chứng minh cấp số nhân: Dãy số \(\left( {{u_n}} \right)\) gồm các số khác 0 thỏa mãn tỉ số \(\frac{{{u_n}}}{{{u_{n - 1}}}}\) không đổi thì dãy số \(\left( {{u_n}} \right)\) là cấp số nhân.
Dãy số \(\left( {{u_n}} \right)\) gồm các số khác 0 thỏa mãn tỉ số \(\frac{{{u_n}}}{{{u_{n - 1}}}}\) không đổi thì dãy số \(\left( {{u_n}} \right)\) là cấp số nhân.
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {2020^n}\). Tính \({u_{n + 1}}\).
-
A.
\({u_{n + 1}} = {2020^n} + 2020\).
-
B.
\({u_{n + 1}} = {2020^{n + 1}}\).
-
C.
\({u_{n + 1}} = {2020^n} + 1\).
-
D.
\({u_{n + 1}} = 2020\left( {n + 1} \right)\).
Đáp án : B
Sử dụng kiến thức số hạng tổng quát của dãy số.
Ta có: \({u_{n + 1}} = {2020^{n + 1}}\)
\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) khi và chỉ khi:
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\) .
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + a} \right) = 0\) .
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}.a} \right) = 0\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 1\).
Đáp án : A
Sử dụng quy tắc về giới hạn dãy số: \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) khi và chỉ khi \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\).
\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) khi và chỉ khi \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Mệnh đề nào đúng?
-
A.
Nếu \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) không có nghiệm trong \(\left( {a;b} \right)\).
-
B.
Nếu \(f\left( a \right).f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm trong \(\left( {a;b} \right)\).
-
C.
Nếu \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm trong \(\left( {a;b} \right)\).
-
D.
Cả A, B, C đều sai.
Đáp án : D
Sử dụng kiến thức hàm số liên tục: Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Nếu \(f\left( a \right).f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm trong \(\left( {a;b} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Nếu \(f\left( a \right).f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm trong \(\left( {a;b} \right)\).
-
A.
\(x = 2\).
-
B.
\(x = 1\).
-
C.
\(x = 0\)
-
D.
\(x = - 1\).
Đáp án : A
Sử dụng kiến thức về hàm số liên tục.
Tại \(x = 2\) thì hàm số không liên tục.
Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = - \infty \) thì:
-
A.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = - \infty \) .
-
B.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = + \infty \).
-
C.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = 0\).
-
D.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = a\).
Đáp án : C
Sử dụng quy tắc tính giới hạn của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = - \infty \) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = 0\).
Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = - \infty \) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = 0\)
Cho hình chóp S. ABCD có O là giao điểm của AC và BD. Gọi M, I lần lượt là trung điểm của BD, SD. Điểm nào dưới đây thuộc mặt phẳng (SOC)?
-
A.
Điểm A .
-
B.
Điểm B.
-
C.
Điểm I.
-
D.
Điểm M.
Đáp án : A
Sử dụng kiến thức về điểm thuộc mặt phẳng.
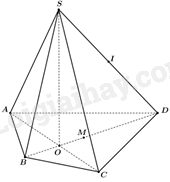
Vì điểm \(A \in OC\) nên điểm A thuộc mặt phẳng (SOC).
Chọn đáp án sai .
-
A.
Trong không gian, có ba đường thẳng phân biệt cùng đi qua hai điểm phân biệt cho trước.
-
B.
Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
-
C.
Có duy nhất một mặt phẳng đi qua ba điểm không thẳng hàng.
-
D.
Nếu một đường thẳng đi qua hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Đáp án : A
Sử dụng kiến thức về đường thẳng và mặt phẳng trong không gian.
Trong không gian, chỉ có một đường thẳng phân biệt đi qua hai điểm phân biệt cho trước nên đáp án A sai.
Với điều kiện nào dưới đây thì đường thẳng d song song với mặt phẳng (P)?
-
A.
a//d, \(a \subset \left( P \right)\) .
-
B.
d//a, a//(P).
-
C.
\(d \cap \left( P \right) = \emptyset \).
-
D.
d//a, \(a \cap \left( P \right) = \emptyset \).
Đáp án : C
Sử dụng kiến thức về đường thẳng song song với mặt phẳng:
+ Nếu d và (P) không có điểm chung thì ta nó d song song với (P).
+ Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong mặt phẳng (P) thì a song song với (P).
Đáp án đúng: \(d \cap \left( P \right) = \emptyset \)
Nếu đường thẳng d và mặt phẳng (P) có … điểm chung thì d cắt mặt phẳng (P).
Từ (cụm từ) thích hợp điền vào “…” để được câu đúng là:
-
A.
duy nhất một.
-
B.
hai.
-
C.
không.
-
D.
vô số.
Đáp án : A
Sử dụng kiến thức về đường thẳng và mặt phẳng trong không gian: Nếu đường thẳng d và mặt phẳng (P) có duy nhất một điểm chung thì d cắt mặt phẳng (P).
Nếu đường thẳng d và mặt phẳng (P) có duy nhất một điểm chung thì d cắt mặt phẳng (P).
Hình chóp S. ABCD có bao nhiêu đỉnh?
-
A.
7 .
-
B.
5.
-
C.
6.
-
D.
8.
Đáp án : B
Sử dụng kiến thức về hình chóp tứ giác: Hình chóp S. ABCD có 5 đỉnh là S, A, B, C, D.
Hình chóp S. ABCD có 5 đỉnh là S, A, B, C, D.
Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa a và cắt mặt phẳng (P) theo giao tuyến b. Kết luận nào sau đây đúng?
-
A.
a và b cắt nhau .
-
B.
a và b trùng nhau .
-
C.
a và b chéo nhau.
-
D.
a và b song song.
Đáp án : D
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa a và cắt mặt phẳng (P) theo giao tuyến b thì b song song với a.
Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa a và cắt mặt phẳng (P) theo giao tuyến b thì b song song với a.
Cho \(\tan \alpha = -2\) và \(\frac{\pi }{2} < \alpha < \pi \). Chọn đáp án đúng.
-
A.
\(\cos \alpha = - \sqrt 5 \) .
-
B.
\(\cos \alpha = \frac{{\sqrt 5 }}{5}\).
-
C.
\(\cos \alpha = \frac{{ - \sqrt 5 }}{5}\).
-
D.
\(\cos \alpha = \sqrt 5 \).
Đáp án : C
Sử dụng công thức: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\).
Vì \(\frac{\pi }{2} < \alpha < \pi \) nên \(\cos \alpha < 0\).
Ta có: \(\frac{1}{{\cos \alpha }} = - \sqrt {1 + {{\tan }^2}\alpha } = - \sqrt 5 \Rightarrow \cos \alpha = \frac{{ - \sqrt 5 }}{5}\).
Rút gọn biểu thức \(A = \frac{{\sin x + \sin 2x + \sin 3x}}{{\cos x + \cos 2x + \cos 3x}}\)
-
A.
\(A = \cot 2x\) .
-
B.
\(A = \tan 2x\).
-
C.
\(A = \sin 2x\).
-
D.
\(A = \cos 2x\).
Đáp án : B
Sử dụng công thức: \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2};\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2};\)
\(A = \frac{{\sin x + \sin 2x + \sin 3x}}{{\cos x + \cos 2x + \cos 3x}} = \frac{{2\sin 2x\cos x + \sin 2x}}{{2\cos 2x\cos x + \cos 2x}} = \frac{{\sin 2x\left( {2\cos x + 1} \right)}}{{\cos 2x\left( {2\cos x + 1} \right)}} = \tan 2x\)
Giá trị của biểu thức \(\sin \frac{{37\pi }}{{12}}\) bằng:
-
A.
\(\frac{{\sqrt 6 - \sqrt 2 }}{4}\) .
-
B.
\( - \frac{{\sqrt 6 + \sqrt 2 }}{4}\).
-
C.
\(\frac{{\sqrt 6 + \sqrt 2 }}{4}\).
-
D.
\(\frac{{ - \sqrt 6 + \sqrt 2 }}{4}\).
Đáp án : D
Sử dụng kiến công thức: \(\sin \left( {a - b} \right) = \sin a\cos b - \cos a\sin b\)
\(\sin \frac{{37\pi }}{{12}} = \sin \left( {2\pi + \pi + \frac{\pi }{{12}}} \right) = \sin \left( {\pi + \frac{\pi }{{12}}} \right) = - \sin \frac{\pi }{{12}} = - \sin \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right)\)
\( = - \left( {\sin \frac{\pi }{3}\cos \frac{\pi }{4} - \cos \frac{\pi }{3}\sin \frac{\pi }{4}} \right) = - \left( {\frac{{\sqrt 3 }}{2}.\frac{{\sqrt 2 }}{2} - \frac{1}{2}.\frac{{\sqrt 2 }}{2}} \right) = \frac{{ - \sqrt 6 + \sqrt 2 }}{4}\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2024\) và \({u_n} = {u_{n - 1}} - 3\) với \(n \ge 2\), \(n \in \mathbb{N}*\). Số hạng tổng quát của cấp số cộng đã cho là:
-
A.
\({u_n} = - 3n - 2027\) với \(n \ge 2\), \(n \in \mathbb{N}*\) .
-
B.
\({u_n} = - 3n + 2027\) với \(n \ge 2\), \(n \in \mathbb{N}*\).
-
C.
\({u_n} = 3n + 2027\) với \(n \ge 2\), \(n \in \mathbb{N}*\).
-
D.
\({u_n} = 3n + 2027\) với \(n \ge 2\), \(n \in \mathbb{N}*\).
Đáp án : B
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số cộng: Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\).
Ta có: \({u_1} = 2024\) và \({u_n} = {u_{n - 1}} - 3\) với \(n \ge 2\), \(n \in \mathbb{N}*\) nên \(d = {u_n} - {u_{n - 1}} = \left( {{u_{n - 1}} - 3} \right) - {u_{n - 1}} = - 3\)
Vậy số hạng tổng quát của cấp số cộng là: \({u_n} = {u_1} + \left( {n - 1} \right)d = 2024 + \left( {n - 1} \right)\left( { - 3} \right) = - 3n + 2027\) với \(n \ge 2\), \(n \in \mathbb{N}*\).
Theo ước tính, kể từ lúc mới mua, cứ sau mỗi 200 lần sạc thì pin của điện thoại X sẽ giảm 4% so với chu kỳ 200 lần sạc trước đó. Hỏi sau 1 200 lần sạc thì pin của điện thoại X còn lại bao nhiêu phần trăm so với lúc mới mua? (làm tròn đến chữ số thập phân thứ hai)
-
A.
78,28% .
-
B.
78,27% .
-
C.
81,54% .
-
D.
81,53% .
Đáp án : A
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số nhân: Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội q thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1}.{q^{n - 1}}\) với \(n \ge 2\).
200 lần sạc tạo thành 1 chu kì, 1200 lần sạc tạo thành 6 chu kì.
Pin điện thoại ban đầu là 100%, sau 1 chu kì còn 96% = 0,96.
Sau chu kì thứ 2, pin chỉ còn 96% so với sau chu kì 1, tức 0,96.0,96 = 0,9216.
…
Như vậy, pin điện thoại sau mỗi chu kì sạc sẽ tạo thành một cấp số nhân có công bội \(q = 0,96\) và số hạng đầu \({u_1} = 100\% \).
Mức pin điện thoại ban đầu là \({u_1} = 100\% \).
Mức pin điện thoại sau 1 chu kì là \({u_2}\).
Mức pin điện thoại sau 2 chu kì là \({u_3}\).
…
Mức pin điện thoại sau 6 chu kì là \({u_7}\).
Dung lượng pin của điện thoại còn lại sau 1200 lần sạc so với lúc mới mua là: \({u_7} = {u_1}.{q^6} = 100\% .{\left( {0,96} \right)^6} \approx 78,28\% \).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 25{n^2} + 10n + 9\). Chọn khẳng định đúng:
-
A.
Dãy số trên bị chặn dưới .
-
B.
Dãy số trên bị chặn trên.
-
C.
Dãy số trên không bị chặn.
-
D.
Dãy số trên bị chặn.
Đáp án : A
Sử dụng kiến thức về dãy số bị chặn:
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn trên nếu tồn tại một số M sao cho \({u_n} \le M\) với mọi \(n \in \mathbb{N}*\)
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn dưới nếu tồn tại một số m sao cho \({u_n} \ge m\) với mọi \(n \in \mathbb{N}*\)
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới.
Ta có: \({u_n} = 25{n^2} + 10n + 9 = \left( {25{n^2} + 10n + 1} \right) + 8 = {\left( {5n + 1} \right)^2} + 8 \ge 8\) với mọi \(n \in \mathbb{N}*\).
Do đó, dãy số \(\left( {{u_n}} \right)\) bị chặn dưới, không bị chặn trên.
Tìm số thực a khác 0 sao cho \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{n^2} - 2}}{{a{n^2} - 1}} = 2\)
-
A.
\(a = - \frac{1}{2}\) .
-
B.
\(a = - 2\).
-
C.
\(a = 2\).
-
D.
\(a = \frac{1}{2}\).
Đáp án : D
Sử dụng kiến thức giới hạn dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b \ne 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\).
Ta có: \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{n^2} - 2}}{{a{n^2} - 1}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{{n^2}\left( {\frac{{{n^2}}}{{{n^2}}} - \frac{2}{{{n^2}}}} \right)}}{{{n^2}\left( {\frac{{a{n^2}}}{{{n^2}}} - \frac{1}{{{n^2}}}} \right)}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{1 - \frac{2}{{{n^2}}}}}{{a - \frac{1}{{{n^2}}}}} = \frac{1}{a}\)
Do đó, \(\frac{1}{a} = 2 \Rightarrow a = \frac{1}{2}\left( {tm} \right)\)
Giới hạn \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} - 18n} - n} \right)\) bằng:
-
A.
9 .
-
B.
\( - 9\).
-
C.
18.
-
D.
\( + \infty \).
Đáp án : B
Sử dụng quy tắc về giới hạn của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b \ne 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\).
\(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} - 18n} - n} \right) = \mathop {\lim }\limits_{n \to + \infty } \frac{{\left( {\sqrt {{n^2} - 18n} - n} \right)\left( {\sqrt {{n^2} - 18n} + n} \right)}}{{\sqrt {{n^2} - 18n} + n}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{ - 18n}}{{\sqrt {{n^2} - 18n} + n}}\)
\( = \mathop {\lim }\limits_{n \to + \infty } \frac{{ - 18n}}{{\sqrt {{n^2} - 18n} + n}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{ - 18}}{{\sqrt {1 - \frac{{18}}{n}} + 1}} = - 9\)
Biểu diễn số thập phân vô hạn tuần hoàn 3,333… dưới dạng phân số ta được:
-
A.
\(\frac{{10}}{3}\) .
-
B.
\(\frac{3}{{10}}\).
-
C.
\(\frac{{100}}{3}\).
-
D.
\(\frac{{100}}{{33}}\).
Đáp án : A
Sử dụng kiến thức về tổng của cấp số nhân lùi vô hạn: Cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với công bội q, số hạng đầu \({u_1}\) thì có tổng là \(S = \frac{{{u_1}}}{{1 - q}}\).
Ta có: \(3,333... = 3 + 0,3 + 0,03 + 0,003 + ... = 3 + 3.\frac{1}{{10}} + 3.\frac{1}{{{{10}^2}}} + 3.\frac{1}{{{{10}^3}}} + ...\)
Đây là cấp số nhân lùi vô hạn với \({u_1} = 3,q = \frac{1}{{10}}\) nên \(3,333... = \frac{3}{{1 - \frac{1}{{10}}}} = \frac{{10}}{3}\)
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của BC, I là giao điểm của AM và BD, \(\left( \alpha \right)\) là mặt phẳng qua A, M và song song với SD. Mặt phẳng \(\left( \alpha \right)\) cắt SB tại N. Tỉ số \(\frac{{SN}}{{SB}}\) là:
-
A.
\(\frac{3}{4}\) .
-
B.
\(\frac{1}{2}\).
-
C.
\(\frac{2}{3}\).
-
D.
\(\frac{1}{3}\).
Đáp án : C
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a song song với b.
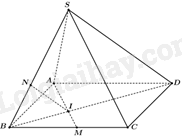
Tam giác ABC có hai đường trung tuyến BD và AM cắt nhau tại I nên I là trọng tâm của tam giác ABC.
Suy ra: \(\frac{{BI}}{{BD}} = \frac{1}{3} \Rightarrow \frac{{ID}}{{BD}} = \frac{2}{3}\)
Vì \(\left( \alpha \right)\) và mặt phẳng (SBD) có điểm chung là I, \(\left( \alpha \right)\)//SD, \(SD \subset \left( {DBD} \right)\) nên giao tuyến của \(\left( \alpha \right)\) và mặt phẳng (SBD) là đường thẳng qua I song song với SD cắt SB tại N. Do đó, \(\frac{{SN}}{{SB}} = \frac{{ID}}{{DB}} = \frac{2}{3}\)
Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD, P là điểm thuộc SA. Giao tuyến của hai mặt phẳng (SAD) và (PMN) là đường thẳng:
-
A.
Qua P song song với AB .
-
B.
Qua P song song với AD.
-
C.
PD.
-
D.
Qua P song song với MC.
Đáp án : B
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
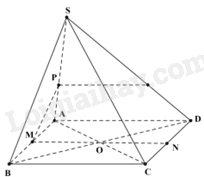
Ta có: \(\left\{ \begin{array}{l}MN//AD\\MN \subset \left( {PMN} \right)\\AD \subset \left( {SAD} \right)\\P \in \left( {PMN} \right) \cap \left( {SAD} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (SAD) và (PMN) là đường thẳng qua P song song với AD.
Cho tứ diện ABCD và điểm M thuộc miền trong tam giác ACD. Gọi I và J lần lượt là hai điểm trên cạnh BC và BD sao cho IJ sao cho IJ không song song với CD. Gọi H là giao điểm của IJ với CD, K là giao điểm của MH và AC. Giao tuyến của hai mặt phẳng (ACD) và (IJM) là:
-
A.
KI .
-
B.
KJ.
-
C.
HI.
-
D.
HM.
Đáp án : D
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó và kí hiệu là \(d = \left( P \right) \cap \left( Q \right)\).
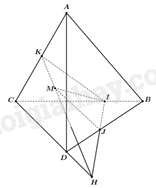
Ta có: M thuộc mặt phẳng (MIJ), M thuộc mặt phẳng (ACD) nên M là điểm chung của mặt phẳng (MIJ) và mặt phẳng (ACD).
Lại có: \(H \in CD \subset \left( {ACD} \right),H \in IJ \subset \left( {IJM} \right) \Rightarrow H \in \left( {IJM} \right) \cap \left( {ACD} \right)\)
Vậy giao tuyến của hai mặt phẳng (ACD) và (IJM) là MH.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, SD. Mặt phẳng (OMN) song song với mặt phẳng nào dưới đây?
-
A.
(SCD).
-
B.
(SBC).
-
C.
(ABCD).
-
D.
(SAB).
Đáp án : B
Sử dụng kiến thức về hai mặt phẳng song song: Nếu trong mặt phẳng (P) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q).
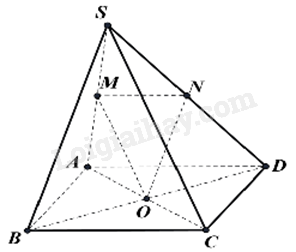
Vì ABCD là hình bình hành tâm O nên O là trung điểm của AC, BD.
Vì MO là đường trung bình của tam giác SAC nên MO//SC nên MO//(SBC)
Vì NO là đường trung bình của tam giác SBD nên ON//SB nên ON//(SBC)
Mà NO và MO cắt nhau tại O trong mặt phẳng (MNO) nên (MON)//(SBC)
Trong mẫu số liệu ghép nhóm, tứ phân vị thứ ba \({Q_3}\) thể hiện:
-
A.
Có 25% số giá trị nhỏ hơn \({Q_3}\) .
-
B.
Có 75% số giá trị nhỏ hơn \({Q_3}\).
-
C.
Có 25% số giá trị lớn hơn \({Q_3}\).
-
D.
Có 75% số giá trị lớn hơn \({Q_3}\).
Đáp án : B
Sử dụng kiến thức về tứ phân vị thứ ba: Trong mẫu số liệu ghép nhóm, tứ phân vị thứ ba \({Q_3}\) thể hiện có 75% số giá trị nhỏ hơn \({Q_3}\).
Trong mẫu số liệu ghép nhóm, tứ phân vị thứ ba \({Q_3}\) thể hiện có 75% số giá trị nhỏ hơn \({Q_3}\).
Trong mẫu số liệu ghép nhóm, độ dài của nhóm \(\left[ {12;15} \right)\) bằng bao nhiêu?
-
A.
12 .
-
B.
15.
-
C.
3.
-
D.
27.
Đáp án : C
Sử dụng kiến thức về độ dài của nhóm trong mẫu số liệu ghép nhóm: Độ dài của nhóm \(\left[ {a;b} \right)\) là \(b - a\).
Độ dài của nhóm \(\left[ {12;15} \right)\) là: \(15 - 12 = 3\)
Cho mẫu số liệu ghép nhóm về thống kê nhiệt độ tại một địa điểm trong 30 ngày như dưới đây:

Nhiệt độ trung bình trong 30 ngày là:
-
A.
22,8\(^oC\) .
-
B.
23\(^oC\).
-
C.
23,2\(^oC\).
-
D.
23,4\(^oC\).
Đáp án : D
Sử dụng kiến thức số trung bình của mẫu số liệu ghép nhóm:
Cho mẫu số liệu ghép nhóm

Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\overline x \): \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\), trong đó \(n = {m_1} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (với \(i = 1;...;k\)) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\).
Nhiệt độ trung bình trong 30 ngày là: \(\frac{{19,5.6 + 22,5.12 + 25,5.9 + 28,5.3}}{{6 + 12 + 9 + 3}} = 23,4\left( {^oC} \right)\)
Mẫu số liệu ghép nhóm dưới đây thống kê doanh thu cửa hàng (triệu) trong tháng như sau:

Mốt của mẫu số liệu này là (làm tròn đến chữ số thập phân thứ nhất):
-
A.
9,2 triệu .
-
B.
9,1 triệu.
-
C.
9,3 triệu.
-
D.
9,4 triệu.
Đáp án : A
Sử dụng kiến thức về tìm mốt của mẫu số liệu ghép nhóm: Để tìm mốt của mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: \(\left[ {{a_j};{a_{j + 1}}} \right)\).
Bước 2: Mốt được xác định là: \({M_o} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\).
Trong đó, \({m_j}\) là tần số của nhóm j, (quy ước \({m_o} = {m_{k + 1}} = 0\)) và h là độ dài của nhóm.
Nhóm chứa mốt của mẫu số liệu trên là \(\left[ {8;10} \right)\).
Ta có: \(j = 3;{a_3} = 8,{m_3} = 18\), \({m_2} = 8;{m_4} = 11,h = 2\). Do đó, \({M_o} = 8 + \frac{{18 - 8}}{{\left( {18 - 8} \right) + \left( {18 - 11} \right)}}.2 \approx 9,2\) (triệu)
Sử dụng quy tắc về giới hạn của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b \ne 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\).
Ta có: \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {4{n^2} - 5n + 8} + a - 2n} \right) = \mathop {\lim }\limits_{n \to + \infty } \frac{{\left( {\sqrt {4{n^2} - 5n + 8} + a - 2n} \right)\left( {\sqrt {4{n^2} - 5n + 8} - \left( {a - 2n} \right)} \right)}}{{\sqrt {4{n^2} - 5n + 8} - \left( {a - 2n} \right)}}\)
\( = \mathop {\lim }\limits_{n \to + \infty } \frac{{\left( {4{n^2} - 5n + 8} \right) - {{\left( {a - 2n} \right)}^2}}}{{\sqrt {4{n^2} - 5n + 8} - \left( {a - 2n} \right)}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{4an - 5n + 8 - {a^2}}}{{\sqrt {4{n^2} - 5n + 8} - \left( {a - 2n} \right)}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{4a - 5 + \frac{8}{n} - \frac{{{a^2}}}{n}}}{{\sqrt {4 - \frac{5}{n} + \frac{8}{{{n^2}}}} - \frac{a}{n} + 2}} = \frac{{4a - 5}}{4}\)
Để \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {4{n^2} - 5n + 8} + a - 2n} \right) = 1\) thì \(\frac{{4a - 5}}{4} = 1 \Leftrightarrow 4a = 9 \Leftrightarrow a = \frac{9}{4}\)
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong mặt phẳng (P) thì a song song với P.
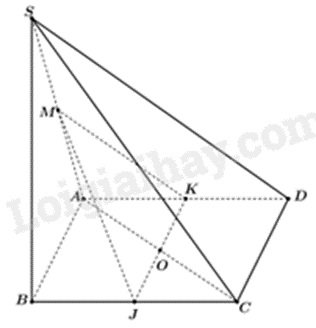
Vì \(\frac{{BC}}{{BJ}} = \frac{{DA}}{{DK}} = 2\) và \(BC = AD\) nên \(BJ = DK\), \(JC = AK\)
Gọi O là giao điểm của AC và JK.
Tam giác JOC có JC//AK nên: \(\frac{{OA}}{{OC}} = \frac{{AK}}{{JC}} = 1\), suy ra O là trung điểm của AC.
Vì M, O lần lượt là trung điểm của SA và AC nên MO là đường trung bình của tam giác SAC.
Do đó, MO//SC, mà \(MO \subset \left( {MJK} \right)\) nên SC//(MJK).
Sử dụng kiến thức: Phương trình \(a\sin x + b\cos x = c\) có nghiệm khi \({a^2} + {b^2} \ge {c^2}\)
Gọi \({y_o}\) là một giá trị của hàm số. Khi đó, phương trình \({y_o} = \frac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}}\) có nghiệm.
Ta có: \({y_o} = \frac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}} \Leftrightarrow \left( {2{y_o} - 1} \right)\cos x - \left( {{y_o} + 2} \right)\sin x = 3 - 4{y_o}\) (1)
Phương trình (1) có nghiệm \( \Leftrightarrow {\left( {2{y_o} - 1} \right)^2} + {\left( {{y_o} + 2} \right)^2} \ge {\left( {3 - 4{y_o}} \right)^2}\)
\( \Leftrightarrow 11y_o^2 - 24{y_o} + 4 \le 0 \Leftrightarrow \frac{2}{{11}} \le {y_o} \le 2\)
Vậy \(\frac{2}{{11}} \le y \le 2\).
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số nhân: Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội q thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1}.{q^{n - 1}},n \ge 2\).
Với mọi \(n \ge 1,n \in \mathbb{N}\) ta có: \({u_{n + 1}} = \frac{{ - {u_n} + 1}}{{2{u_n}}} \Rightarrow {u_{n + 1}} + 1 = \frac{{ - {u_n} + 1}}{{2{u_n}}} + 1 = \frac{{{u_n} + 1}}{{2{u_n}}}\)
\( \Rightarrow \frac{1}{{{u_{n + 1}} + 1}} = \frac{{2{u_n}}}{{{u_n} + 1}} = - \frac{2}{{{u_n} + 1}} + 2 \Rightarrow \frac{1}{{{u_{n + 1}} + 1}} - \frac{2}{3} = - \frac{2}{{{u_n} + 1}} + \frac{4}{3} = - 2\left( {\frac{1}{{{u_n} + 1}} - \frac{2}{3}} \right)\)
Đặt \({v_n} = \frac{1}{{{u_n} + 1}} - \frac{2}{3}\) với mọi \(n \ge 1,n \in \mathbb{N}\) \( \Rightarrow \left\{ \begin{array}{l}{v_{n + 1}} = \frac{1}{{{u_{n + 1}} + 1}} - \frac{2}{3},n \ge 1,n \in \mathbb{N}\\{v_1} = \frac{1}{{{u_1} + 1}} - \frac{2}{3} = \frac{{ - 1}}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{v_{n + 1}} = - 2{v_n},n \ge 1,n \in \mathbb{N}\\{v_1} = \frac{{ - 1}}{3}\end{array} \right.\)
Do đó, \(\left( {{v_n}} \right)\) là một cấp số nhân với số hạng đầu \({v_1} = \frac{{ - 1}}{3}\) và công bội \(q = - 2\)
Số hạng tổng quát của \(\left( {{v_n}} \right)\) là: \({v_n} = {v_1}.{q^{n - 1}} = \frac{{ - 1}}{3}{\left( { - 2} \right)^{n - 1}}\)
\( \Rightarrow \frac{1}{{{u_n} + 1}} - \frac{2}{3} = - \frac{1}{3}{\left( { - 2} \right)^{n - 1}} \Rightarrow \frac{1}{{{u_n} + 1}} = \frac{2}{3} - \frac{1}{3}{\left( { - 2} \right)^{n - 1}}\)\( \Rightarrow {u_n} = \frac{1}{{\frac{2}{3} - \frac{1}{3}{{\left( { - 2} \right)}^{n - 1}}}} - 1 = \frac{{\frac{1}{3} + \frac{1}{3}{{\left( { - 2} \right)}^{n - 1}}}}{{\frac{2}{3} - \frac{1}{3}{{\left( { - 2} \right)}^{n - 1}}}} = \frac{{1 + {{\left( { - 2} \right)}^{n - 1}}}}{{2 - {{\left( { - 2} \right)}^{n - 1}}}}\)
Vậy số hạng tổng quát của dãy số đã cho là: \({u_n} = \frac{{1 + {{\left( { - 2} \right)}^{n - 1}}}}{{2 - {{\left( { - 2} \right)}^{n - 1}}}}\)