Trắc nghiệm Bài 24: Phép nhân và phép chia phân thức đại số Toán 8 Kết nối tri thức
Đề bài
Phương trình với ẩn x có dạng:
-
A.
\(A\left( x \right) = B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
B.
\(A\left( x \right) > B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
C.
\(A\left( x \right) < B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
D.
\(A\left( x \right) \ge B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
Phương trình nào dưới đây là phương trình một ẩn?
-
A.
\(2x - 2y + 1 = 0\)
-
B.
\(xzy = 6\)
-
C.
\(2{x^2} + 1 = x - 2\)
-
D.
\(3{x^2} + 4{y^2} = 2y\)
\({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu:
-
A.
\(A\left( {{x_0}} \right) < B\left( {{x_0}} \right)\)
-
B.
\(A\left( {{x_0}} \right) > B\left( {{x_0}} \right)\)
-
C.
\(A\left( {{x_0}} \right) \ne B\left( {{x_0}} \right)\)
-
D.
\(A\left( {{x_0}} \right) = B\left( {{x_0}} \right)\)
Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho được gọi là phương trình bậc nhất một ẩn x khi:
-
A.
Với mọi giá trị của a, b
-
B.
\(a \ne 0;b \ne 0\)
-
C.
\(a \ne 0\)
-
D.
\(b \ne 0\)
Cho phương trình \(2x + 1 = 0\), chọn khẳng định đúng
-
A.
Hệ số của x là 2, hạng tử tự do là 1
-
B.
Hệ số của x là 1, hạng tử tự do là 2
-
C.
Hệ số của x là \( - 1,\) hạng tử tự do là 2
-
D.
Hệ số của x là 2, hạng tử tự do là \( - 1\)
Nghiệm của phương trình \(3x - 6 = 0\) là:
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = \frac{{ - 1}}{2}\)
-
C.
\(x = 2\)
-
D.
\(x = - 2\)
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
-
A.
\(a + b = 21\)
-
B.
\(a + b = 23\)
-
C.
\(a + b = 20\)
-
D.
\(a + b = 24\)
Ở một số quốc gia, người ta dùng cả hai đơn vị đo nhiệt độ là Fahrenheit ( o F) và độ Celcius ( o C), liên hệ với nhau bởi công thức \(C = \frac{5}{9}\left( {F - 32} \right).\) Khi ở 20 o C thì ứng với độ Fahrenheit là:
-
A.
34 o F
-
B.
38 o F
-
C.
64 o F
-
D.
68 o F
Biết rằng \(4x - 8 = 0\). Giá trị của biểu thức \(5{x^2} - 4\) là:
-
A.
\( - 24\)
-
B.
\(24\)
-
C.
\( - 16\)
-
D.
16
Phương trình \({x^2} + 4 = 0\) có bao nhiêu nghiệm?
-
A.
Vô nghiệm
-
B.
Vô số nghiệm
-
C.
1 nghiệm
-
D.
2 nghiệm
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = - \frac{1}{2}\)
-
C.
\(x = \frac{1}{4}\)
-
D.
\(x = \frac{{ - 1}}{4}\)
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
-
A.
\({x_0} < 0\)
-
B.
\({x_0} < - 1\)
-
C.
\({x_0} > 0\)
-
D.
\({x_0} > 1\)
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
-
A.
\(x = 1\)
-
B.
\(x = - 1\)
-
C.
\(x = - 2\)
-
D.
\(x = 2\)
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
-
A.
Phương trình (1) vô nghiệm, phương trình (2) có nghiệm duy nhất
-
B.
Phương trình (1) có vô số nghiệm, phương trình (2) vô nghiệm
-
C.
Phương trình (1) vô nghiệm, phương trình (2) có vô số nghiệm
-
D.
Cả phương trình (1) và phương trình (2) đều có một nghiệm
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
-
A.
Nghiệm của phương trình là một chia hết cho 5
-
B.
Nghiệm của phương trình là một số chia hết cho 2
-
C.
Nghiệm của phương trình là một chia hết cho 4
-
D.
Nghiệm của phương trình là một số nguyên tố
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
-
A.
\(m \ne \frac{4}{3}\)
-
B.
\(m = \frac{4}{3}\)
-
C.
\(m = \frac{3}{4}\)
-
D.
\(m \ne \frac{3}{4}\)
-
A.
\(x = - 2\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = - 1\)
Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
-
A.
\(a = 7\)
-
B.
\(a = - 7\)
-
C.
\(a = \frac{1}{7}\)
-
D.
\(a = \frac{{ - 1}}{7}\)
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
Không có nghiệm nào
-
D.
Có vô số nghiệm
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:
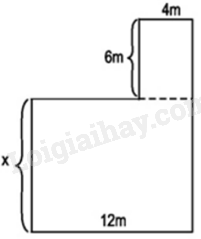
-
A.
11m
-
B.
12m
-
C.
13m
-
D.
14m
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
-
A.
\(48 = 32\left( {x - 1} \right)\)
-
B.
\(48x = 32\left( {1 - x} \right)\)
-
C.
\(48x = 32\left( {x - 1} \right)\)
-
D.
\(48x = 32\left( {x + 1} \right)\)
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
-
A.
\(m = 1\)
-
B.
\(m = 2\)
-
C.
\(m \in \left\{ {1;2} \right\}\)
-
D.
\(m = 0\)
Số nghiệm của phương trình \(\sqrt x + 1 = 2\sqrt { - x} \) là:
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
0 nghiệm
-
D.
Vô số nghiệm
Hình dưới dây mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1ft=0,3048m). Tốc độ v(ft/s) của nước tại thời điểm t(s) được cho bởi công thức \(v = 48 - 30t.\) Thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:

-
A.
1,8s
-
B.
1,7s
-
C.
1,6s
-
D.
1,5s
Nghiệm của phương trình \(\frac{{x + a}}{{b + c}} + \frac{{x + b}}{{a + c}} + \frac{{x + c}}{{a + b}} = - 3\) (các mẫu đều khác 0) là:
-
A.
\(x = a + b + c\)
-
B.
\(x = a - b - c\)
-
C.
\(x = a + b - c\)
-
D.
\(x = - \left( {a + b + c} \right)\)
Cho a và ba số b, c, d khác a thỏa mãn điều kiện \(b + d = 2c.\) Số nghiệm của phương trình \(\frac{x}{{\left( {a - b} \right)\left( {a - c} \right)}} - \frac{{2x}}{{\left( {a - b} \right)\left( {a - d} \right)}} + \frac{{3x}}{{\left( {a - c} \right)\left( {a - d} \right)}} = \frac{{4a}}{{\left( {a - c} \right)\left( {a - d} \right)}}\) là:
-
A.
0 nghiệm
-
B.
1 nghiệm
-
C.
2 nghiệm
-
D.
Vô số nghiệm
Lời giải và đáp án
Phương trình với ẩn x có dạng:
-
A.
\(A\left( x \right) = B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
B.
\(A\left( x \right) > B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
C.
\(A\left( x \right) < B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
D.
\(A\left( x \right) \ge B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
Đáp án : A
Phương trình nào dưới đây là phương trình một ẩn?
-
A.
\(2x - 2y + 1 = 0\)
-
B.
\(xzy = 6\)
-
C.
\(2{x^2} + 1 = x - 2\)
-
D.
\(3{x^2} + 4{y^2} = 2y\)
Đáp án : C
\({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu:
-
A.
\(A\left( {{x_0}} \right) < B\left( {{x_0}} \right)\)
-
B.
\(A\left( {{x_0}} \right) > B\left( {{x_0}} \right)\)
-
C.
\(A\left( {{x_0}} \right) \ne B\left( {{x_0}} \right)\)
-
D.
\(A\left( {{x_0}} \right) = B\left( {{x_0}} \right)\)
Đáp án : D
Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho được gọi là phương trình bậc nhất một ẩn x khi:
-
A.
Với mọi giá trị của a, b
-
B.
\(a \ne 0;b \ne 0\)
-
C.
\(a \ne 0\)
-
D.
\(b \ne 0\)
Đáp án : C
Cho phương trình \(2x + 1 = 0\), chọn khẳng định đúng
-
A.
Hệ số của x là 2, hạng tử tự do là 1
-
B.
Hệ số của x là 1, hạng tử tự do là 2
-
C.
Hệ số của x là \( - 1,\) hạng tử tự do là 2
-
D.
Hệ số của x là 2, hạng tử tự do là \( - 1\)
Đáp án : A
Nghiệm của phương trình \(3x - 6 = 0\) là:
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = \frac{{ - 1}}{2}\)
-
C.
\(x = 2\)
-
D.
\(x = - 2\)
Đáp án : C
\(3x - 6 = 0\)
\(3x = 6\)
\(x = \frac{6}{3} = 2\)
Vậy phương trình có nghiệm \(x = 2\)
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
-
A.
\(a + b = 21\)
-
B.
\(a + b = 23\)
-
C.
\(a + b = 20\)
-
D.
\(a + b = 24\)
Đáp án : B
\(\frac{3}{4} + \frac{2}{5}x = 0\)
\(\frac{2}{5}x = \frac{{ - 3}}{4}\)
\(x = \frac{{ - 3}}{4}:\frac{2}{5} = \frac{{ - 15}}{8}\)
Do đó, \(a = 15,b = 8\)
Vậy \(a + b = 15 + 8 = 23\)
Ở một số quốc gia, người ta dùng cả hai đơn vị đo nhiệt độ là Fahrenheit ( o F) và độ Celcius ( o C), liên hệ với nhau bởi công thức \(C = \frac{5}{9}\left( {F - 32} \right).\) Khi ở 20 o C thì ứng với độ Fahrenheit là:
-
A.
34 o F
-
B.
38 o F
-
C.
64 o F
-
D.
68 o F
Đáp án : D
Với \(C = {20^o}C\) ta có:
\(20 = \frac{5}{9}\left( {F - 32} \right)\)
\(F - 32 = 20 : \frac{5}{9}\)
\(F - 32 = 36\)
\(F = 36 + 32 = 68\)
Vậy \(C = {20^o}C\) thì ứng với 68 o F
Biết rằng \(4x - 8 = 0\). Giá trị của biểu thức \(5{x^2} - 4\) là:
-
A.
\( - 24\)
-
B.
\(24\)
-
C.
\( - 16\)
-
D.
16
Đáp án : D
\(4x - 8 = 0\)
\(4x = 8\)
\(x = \frac{8}{4} = 2\)
Với \(x = 2\) thay vào biểu thức \(5{x^2} - 4\) ta có: \({5.2^2} - 4 = 16\)
Phương trình \({x^2} + 4 = 0\) có bao nhiêu nghiệm?
-
A.
Vô nghiệm
-
B.
Vô số nghiệm
-
C.
1 nghiệm
-
D.
2 nghiệm
Đáp án : A
Vì \({x^2} \ge 0\) với mọi x nên \({x^2} + 4 > 0\) với mọi x.
Do đó, phương trình \({x^2} + 4 = 0\) vô nghiệm.
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = - \frac{1}{2}\)
-
C.
\(x = \frac{1}{4}\)
-
D.
\(x = \frac{{ - 1}}{4}\)
Đáp án : A
Theo đề bài ta có: \(\left( {x - \frac{1}{4}} \right).\frac{1}{2} = \frac{1}{8}\)
\(x - \frac{1}{4} = \frac{1}{8}:\frac{1}{2} = \frac{1}{4}\)
\(x = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\)
Vậy \(x = \frac{1}{2}\)
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
-
A.
\({x_0} < 0\)
-
B.
\({x_0} < - 1\)
-
C.
\({x_0} > 0\)
-
D.
\({x_0} > 1\)
Đáp án : A
\(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}\)
\(3x - 15 + 9{x^2} - 27x = 9{x^2}\)
\( - 24x = 15\)
\(x = \frac{{ - 5}}{8}\)
Khi đó, nghiệm của phương là \({x_0} = \frac{{ - 5}}{8}\)
Do đó, \({x_0} < 0\)
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
-
A.
\(x = 1\)
-
B.
\(x = - 1\)
-
C.
\(x = - 2\)
-
D.
\(x = 2\)
Đáp án : B
Vì \(A = B\) nên \(\frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2} = \frac{{1 + 3x}}{4}\)
\(\frac{{8\left( {x + 1} \right)}}{{12}} - \frac{6}{{12}} = \frac{{3\left( {1 + 3x} \right)}}{{12}}\)
\(8x + 8 - 6 = 3 + 9x\)
\(9x - 8x = 2 - 3\)
\(x = - 1\)
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
-
A.
Phương trình (1) vô nghiệm, phương trình (2) có nghiệm duy nhất
-
B.
Phương trình (1) có vô số nghiệm, phương trình (2) vô nghiệm
-
C.
Phương trình (1) vô nghiệm, phương trình (2) có vô số nghiệm
-
D.
Cả phương trình (1) và phương trình (2) đều có một nghiệm
Đáp án : C
\(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\)
\(8x - 16 = 14 + 6x - 6 + 2x + 10\)
\(8x - 6x - 2x = 18 + 16\)
\(0 = 34\) (vô lí)
Vậy phương trình (1) vô nghiệm.
\({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\)
\({x^2} - 4x + 4 = {x^2} - 2x - 2x + 4\)
\({x^2} - 4x + 4 - {x^2} + 4x - 4 = 0\)
\(0 = 0\) (luôn đúng)
Vậy phương trình (2) có vô số nghiệm.
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
-
A.
Nghiệm của phương trình là một chia hết cho 5
-
B.
Nghiệm của phương trình là một số chia hết cho 2
-
C.
Nghiệm của phương trình là một chia hết cho 4
-
D.
Nghiệm của phương trình là một số nguyên tố
Đáp án : B
\(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\)
\(\left( {\frac{{x - 11}}{{2011}} - 1} \right) + \left( {\frac{{x - 10}}{{2012}} - 1} \right) = \left( {\frac{{x - 74}}{{1948}} - 1} \right) + \left( {\frac{{x - 72}}{{1950}} - 1} \right)\)
\(\frac{{x - 2022}}{{2011}} + \frac{{x - 2022}}{{2012}} - \frac{{x - 2022}}{{1948}} - \frac{{x - 2022}}{{1950}} = 0\)
\(\left( {x - 2022} \right)\left( {\frac{1}{{2011}} + \frac{1}{{2012}} - \frac{1}{{1948}} - \frac{1}{{1950}}} \right) = 0\)
\(x - 2022 = 0\) (vì \(\frac{1}{{2011}} + \frac{1}{{2012}} - \frac{1}{{1948}} - \frac{1}{{1950}} < 0\))
\(x = 2022\)
Vì 2022 chia hết cho 2, không chia hết cho 4, không chia hết cho 5 nên nghiệm của phương trình là một số chia hết cho 2
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
-
A.
\(m \ne \frac{4}{3}\)
-
B.
\(m = \frac{4}{3}\)
-
C.
\(m = \frac{3}{4}\)
-
D.
\(m \ne \frac{3}{4}\)
Đáp án : A
+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng khái niệm phương trình bậc nhất một ẩn: Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho và \(a \ne 0\) được gọi là phương trình bậc nhất một ẩn x.
\(3mx + m - 4x = 3{m^2} + 1\)
\(\left( {3m - 4} \right)x + m - 3{m^2} - 1 = 0\)
Để phương trình \(\left( {3m - 4} \right)x + m - 3{m^2} - 1 = 0\) có nghiệm duy nhất thì \(3m - 4 \ne 0\)
\(3m \ne 4\)
\(m \ne \frac{4}{3}\)
Vậy \(m \ne \frac{4}{3}\)
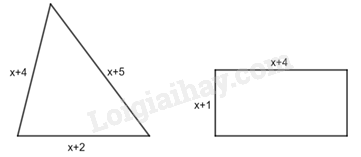
-
A.
\(x = - 2\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = - 1\)
Đáp án : C
+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng chu vi hình tam giác: Chu vi hình tam giác bằng tổng độ dài ba cạnh của tam giác
+ Sử dụng chu vi hình chữ nhật: Chu vi hình tam giác bằng hai lần tổng chiều dài và chiều rộng
Chu vi hình tam giác là: \(x + 2 + x + 4 + x + 5 = 3x + 11\)
Chu vi hình chữ nhật là: \(2\left( {x + 1 + x + 4} \right) = 2\left( {2x + 5} \right) = 4x + 10\)
Vì hai hình có chu vi bằng nhau nên: \(3x + 11 = 4x + 10\)
\(4x - 3x = 11 - 10\)
\(x = 1\)
Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
-
A.
\(a = 7\)
-
B.
\(a = - 7\)
-
C.
\(a = \frac{1}{7}\)
-
D.
\(a = \frac{{ - 1}}{7}\)
Đáp án : A
+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng khái niệm nghiệm của phương trình: Số \({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu giá trị của A(x) và B(x) tại \({x_0}\) bằng nhau.
\(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\)
\(\frac{{21x}}{{24}} - \frac{{120\left( {x - 9} \right)}}{{24}} = \frac{{4\left( {20x + 1,5} \right)}}{{24}}\)
\(21x - 120x + 1080 = 80x + 6\)
\( - 179x = - 1074\)
\(x = 6\)
Vì phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) nên phương trình (2) có nghiệm là \(x = 2\)
\(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Với \(x = 2\) thay vào phương trình (2) ta có:
\(2\left( {a - 1} \right)2 - a\left( {2 - 1} \right) = 2a + 3\)
\(4a - 4 - a = 2a + 3\)
\(a = 7\)
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
Không có nghiệm nào
-
D.
Có vô số nghiệm
Đáp án : D
\(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\)
\(\frac{{4\left( {x + 1} \right)}}{{12}} + \frac{{9\left( {2x + 1} \right)}}{{12}} = \frac{{2\left( {5x + 3} \right)}}{{12}} + \frac{{7 + 12x}}{{12}}\)
\(4x + 4 + 18x + 9 = 10x + 6 + 7 + 12x\)
\(22x + 13 = 22x + 13\)
\(0 = 0\) (luôn đúng)
Vậy phương trình đã cho có vô số nghiệm
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:

-
A.
11m
-
B.
12m
-
C.
13m
-
D.
14m
Đáp án : B
Hình bên có gồm hai hình chữ nhật:
+ Hình chữ nhật độ dài 2 kích thước là 12m và x (mét) nên diện tích hình là: \(12x\left( {{m^2}} \right)\)
+ Hình chữ nhật có độ dài 2 kích thước là 6m và 4m nên diện tích hình là: \(4.6 = 24\left( {{m^2}} \right)\)
Mà diện tích của cả hình đó bằng \(168{m^2}\) nên ta có:
\(12x + 24 = 168\)
\(12x = 144\)
\(x = 12\)
Vậy \(x = 12m\)
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
-
A.
\(48 = 32\left( {x - 1} \right)\)
-
B.
\(48x = 32\left( {1 - x} \right)\)
-
C.
\(48x = 32\left( {x - 1} \right)\)
-
D.
\(48x = 32\left( {x + 1} \right)\)
Đáp án : D

Giả sử ô tô gặp xe máy tại C như trên hình.
Gọi x (giờ) (x > 0) là khoảng thời gian chuyển động của ôtô đi từ A đến C.
Ô tô đi với vận tốc 48km/h nên quãng đường AC bằng: 48.x (km) (1)
Vì xe máy đi trước ôtô 1 giờ nên thời gian xe máy đi từ A đến C bằng: x + 1 (h)
Xe máy đi với vận tốc 32km/h nên quãng đường AC bằng: 32(x + 1) (km) (2)
Từ (1) và (2) ta có phương trình: 48x = 32(x + 1).
Vậy phương trình là: 48x = 32(x + 1).
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
-
A.
\(m = 1\)
-
B.
\(m = 2\)
-
C.
\(m \in \left\{ {1;2} \right\}\)
-
D.
\(m = 0\)
Đáp án : B
\(\left( {{m^2} - 3m + 2} \right)x = m - 2\left( * \right)\)
Xét \({m^2} - 3m + 2 = 0\)
\({m^2} - m - 2m + 2 = 0\)
\(\left( {m - 1} \right)\left( {m - 2} \right) = 0\)
Từ đó tính được \(m = 1;m = 2\)
Với \(m = 1\) thay vào (*) ta có: \(0.x = - 1\) (vô lí) nên phương trình (*) vô nghiệm.
Với \(m = 2\) thay vào (*) ta có: \(0x = 0\) (luôn đúng) nên phương trình (*) có vô số nghiệm với mọi số thực x.
Số nghiệm của phương trình \(\sqrt x + 1 = 2\sqrt { - x} \) là:
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
0 nghiệm
-
D.
Vô số nghiệm
Đáp án : C
Khi \(x = 0\) ta có: \(1 = 0\) (vô lí) nên \(x = 0\) không là nghiệm của phương trình đã cho
Khi \(x < 0\) thì \(\sqrt x \) không xác định
Khi \(x > 0\) thì \(\sqrt { - x} \) không xác định
Vậy trong mọi trường hợp, không có giá trị nào thỏa mãn phương trình.
Vậy phương trình đã cho vô nghiệm
Hình dưới dây mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1ft=0,3048m). Tốc độ v(ft/s) của nước tại thời điểm t(s) được cho bởi công thức \(v = 48 - 30t.\) Thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:

-
A.
1,8s
-
B.
1,7s
-
C.
1,6s
-
D.
1,5s
Đáp án : C
Khi xuất phát từ mặt đài phun nước, giọt nước có \(t = 0.\)
Khi giọt nước đạt độ cao tối đa thì \(v = 0.\) Thay vào công thức ta có:
\(0 = 48 - 30t\)
\(30t = 48\)
\(t = 1,6\)
Vậy thời gian để giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là: \(1,6 - 0 = 1,6\) (s)
Nghiệm của phương trình \(\frac{{x + a}}{{b + c}} + \frac{{x + b}}{{a + c}} + \frac{{x + c}}{{a + b}} = - 3\) (các mẫu đều khác 0) là:
-
A.
\(x = a + b + c\)
-
B.
\(x = a - b - c\)
-
C.
\(x = a + b - c\)
-
D.
\(x = - \left( {a + b + c} \right)\)
Đáp án : D
\(\frac{{x + a}}{{b + c}} + \frac{{x + b}}{{a + c}} + \frac{{x + c}}{{a + b}} = - 3\)
\(\left( {\frac{{x + a}}{{b + c}} + 1} \right) + \left( {\frac{{x + b}}{{a + c}} + 1} \right) + \left( {\frac{{x + c}}{{a + b}} + 1} \right) = 0\)
\(\frac{{x + a + b + c}}{{b + c}} + \frac{{x + a + b + c}}{{a + c}} + \frac{{x + a + b + c}}{{a + b}} = 0\)
\(\left( {x + a + b + c} \right)\left( {\frac{1}{{b + c}} + \frac{1}{{c + a}} + \frac{1}{{a + b}}} \right) = 0\)
\(x + a + b + c = 0\)
\(x = - \left( {a + b + c} \right)\)
Vậy nghiệm của phương trình đã cho là \(x = - \left( {a + b + c} \right)\)
Cho a và ba số b, c, d khác a thỏa mãn điều kiện \(b + d = 2c.\) Số nghiệm của phương trình \(\frac{x}{{\left( {a - b} \right)\left( {a - c} \right)}} - \frac{{2x}}{{\left( {a - b} \right)\left( {a - d} \right)}} + \frac{{3x}}{{\left( {a - c} \right)\left( {a - d} \right)}} = \frac{{4a}}{{\left( {a - c} \right)\left( {a - d} \right)}}\) là:
-
A.
0 nghiệm
-
B.
1 nghiệm
-
C.
2 nghiệm
-
D.
Vô số nghiệm
Đáp án : B
\(\frac{x}{{\left( {a - b} \right)\left( {a - c} \right)}} - \frac{{2x}}{{\left( {a - b} \right)\left( {a - d} \right)}} + \frac{{3x}}{{\left( {a - c} \right)\left( {a - d} \right)}} = \frac{{4a}}{{\left( {a - c} \right)\left( {a - d} \right)}}\)
\(\frac{{x\left( {a - d} \right) - 2x\left( {a - c} \right) + 3x\left( {a - b} \right)}}{{\left( {a - b} \right)\left( {a - c} \right)\left( {a - d} \right)}} = \frac{{4a\left( {a - b} \right)}}{{\left( {a - b} \right)\left( {a - c} \right)\left( {a - d} \right)}}\)
\(x\left( {a - d - 2a + 2c + 3a - 3b} \right) = 4a\left( {a - b} \right)\)
\(x\left( {2a - 3b + 2c - d} \right) = 4a\left( {a - b} \right)\;\left( 1 \right)\)
Từ giả thiết, \(b + d = 2c\) nên \(2a - 3b + 2c - d = 2a - 2b = 2\left( {a - b} \right)\) thay vào (1) ta có:
\(2\left( {a - b} \right)x = 4a\left( {a - b} \right)\;\left( 2 \right)\)
Vì \(a - b \ne 0\) nên phương trình (2) có nghiệm duy nhất là \(x = 2a.\)
Vậy phương trình đã cho có một nghiệm.