Trắc nghiệm Bài 1: Góc và cạnh của một tam giác Toán 7 Chân trời sáng tạo
Đề bài
-
A.
\(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \)
-
B.
\(\widehat {CAD} + \widehat {BAD} + \widehat {BAC} = 180^\circ \)
-
C.
\(\widehat {CAD} + \widehat {ADC} + \widehat {ACB} = 180^\circ \)
-
D.
\(\widehat {BAC} + \widehat {ACD} + \widehat {ABD} = 180^\circ \)
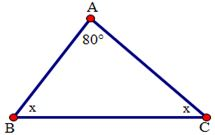
Cho tam giác ABC có \(\widehat A = 86^\circ ;\widehat B = 62^\circ \). Số đo góc C là:
-
A.
\({32^0}\)
-
B.
\({35^0}\)
-
C.
\(24^\circ \)
-
D.
\({90^0}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({100^0}\)
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc C cắt cạnh AB tại M. Số đo góc BMC là:
-
A.
\({50^0}\)
-
B.
\(80^\circ \)
-
C.
\({100^0}\)
-
D.
\({90^0}\)
Tam giác ABC có \(\widehat A = {80^0},\widehat B - \widehat C = {50^0}\). Số đo góc B và góc C lần lượt là:
-
A.
\(\widehat B = {65^0},\widehat C = {15^0}\)
-
B.
\(\widehat B = {75^0},\widehat C = {25^0}\)
-
C.
\(\widehat B = {70^0},\widehat C = {20^0}\)
-
D.
\(\widehat B = {80^0},\widehat C = {30^0}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({70^0}\)
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác của các góc ACE và DBE cắt nhau ở K. Tính số đo góc BKC?
-
A.
90\(^\circ \)
-
B.
\(\widehat {BDC} - \widehat {BAC}\)
-
C.
\(\frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
-
D.
\(\widehat {BDC} + \widehat {BAC}\)
Tam giác ABC có \(\widehat B + \widehat C = \widehat A\) và \(\widehat C = 2\widehat B\). Tia phân giác của góc C cắt AB ở D. Tính \(\widehat {ADC}\)
-
A.
60\(^\circ \)
-
B.
90\(^\circ \)
-
C.
120\(^\circ \)
-
D.
30\(^\circ \)
Khẳng định nào sau đây là sai?
-
A.
Tam giác tù là tam giác có 1 góc tù
-
B.
Tam giác nhọn là tam giác có 3 góc đều là góc nhọn
-
C.
Góc lớn nhất trong 1 tam giác là góc tù
-
D.
2 góc nhọn trong tam giác vuông phụ nhau.
-
A.
\({90^0}\)
-
B.
\({100^0}\)
-
C.
\({120^0}\)
-
D.
\({130^0}\)
Cho tam giác \(ABH\) vuông tại \(H\,\left( {\widehat A > \widehat B} \right).\) Kẻ đường cao \(HC\,\,\left( {C \in AB} \right).\) So sánh \(BH\) và \(AH;\,CH\) và \(CB.\)
-
A.
\(BH > AH;\,\,CB < CH\)
-
B.
\(BH > AH;\,\,CB > CH\)
-
C.
\(BH < AH;\,\,CB < CH\)
-
D.
\(BH < AH;\,\,CB > CH\)
Cho tam giác $ABC,$ biết \(\widehat A:\widehat B:\widehat C = 3:5:7.\) So sánh các cạnh của tam giác.
-
A.
\(AC < AB < BC\)
-
B.
\(BC > AC > AB\)
-
C.
\(BC < AC < AB\)
-
D.
\(BC = AC < AB\)
Cho tam giác $ABC$ cân ở $A$ có chu vi bằng $16cm,$ cạnh đáy $BC = 4cm.$ So sánh các góc của tam giác $ABC.$
-
A.
\(\widehat C = \widehat B > \widehat A\)
-
B.
\(\widehat A = \widehat B > \widehat C\)
-
C.
$\widehat C > \widehat B > \widehat A$
-
D.
\(\widehat C < \widehat B < \widehat A\)
Cho \(\Delta ABC\) cân tại $A.$ Trên $BC$ lấy hai điểm $D$ và $E$ sao cho \(BD = DE = EC\). Chọn câu đúng.
-
A.
\(\widehat {BAD} = \widehat {EAC}\)
-
B.
\(\widehat {EAC} < \widehat {DAE}\)
-
C.
\(\widehat {BAD} < \widehat {DAE}\)
-
D.
Cả A, B, C đều đúng.
Cho \(\Delta ABC\) có $AB > AC$ . Kẻ $BN$ là tia phân giác của góc $B$ \(\left( {N \in AC} \right)\). Kẻ $CM$ là tia phân giác của góc $C$\(\left( {M \in AB} \right)\), $CM$ và $BN$ cắt nhau tại $I.$ So sánh $IC$ và $IB?$
-
A.
\(IB < IC\)
-
B.
\(IC > IB\)
-
C.
\(IB = IC\)
-
D.
\(IB > IC\)
Cho \(\Delta ABC\) có \(AB < AC\) . Gọi $M$ là trung điểm của $BC.$ Trên tia đối của tia $MA$ lấy điểm $D$ sao cho $MA{\rm{ }} = {\rm{ }}MD$. So sánh \(\widehat {CDA}\) và \(\widehat {CAD}\) ?
-
A.
\(\widehat {CAD} > \widehat {CDA}\)
-
B.
\(\widehat {CAD} = \widehat {CDA}\)
-
C.
$\widehat {CAD} < \widehat {CDA}$
-
D.
\(\widehat {CDA} < \widehat {CAD}\)
Cho tam giác \(ABC\) có góc \(A\) tù. Trên cạnh \(AB\) lấy điểm \(E,\) trên cạnh \(AC\) lấy điểm \(F.\) Chọn câu đúng.
-
A.
\(BF > EF\)
-
B.
\(EF < BC\)
-
C.
\(BF < BC\)
-
D.
Cả A, B, C đều đúng
Cho tam giác \(ABC\) có \(\widehat C > \widehat B\) (\(\widehat B,\,\widehat C\) là các góc nhọn). Vẽ phân giác \(AD.\) So sánh \(BD\) và \(CD.\)
-
A.
Chưa đủ điều kiện để so sánh
-
B.
\(BD = CD\)
-
C.
\(BD < CD\)
-
D.
\(BD > CD\)
Cho \(\Delta ABC\) có \(\widehat A = {70}\), \(\widehat B - \widehat C = {30^0}\) . Em hãy chọn câu trả lời đúng nhất:
-
A.
\(AC < AB < BC\)
-
B.
\(AB < AC = BC\)
-
C.
\(BC < AC = AB\)
-
D.
\(AC < BC < AB\)
Cho \(\Delta ABC\) có \(AB + AC = 10cm,AC - AB = 4cm\). So sánh \(\widehat B\) và \(\widehat C\)?
-
A.
\(\widehat C < \widehat B\)
-
B.
$\widehat C > \widehat B$
-
C.
\(\widehat C = \widehat B\)
-
D.
\(\widehat B < \widehat C\)
Chọn câu trả lời đúng. Ba cạnh của tam giác có độ dài là \(6cm;\,7cm;\,8cm.\) Góc lớn nhất là góc
-
A.
đối diện với cạnh có độ dài \(6\,cm.\)
-
B.
đối diện với cạnh có độ dài \(7\,cm.\)
-
C.
đối diện với cạnh có độ dài \(8\,cm.\)
-
D.
Ba cạnh có độ dài bằng nhau.
Cho tam giác $ABC$ có \(\widehat B = {90^0}\), \(\widehat A = {35^0}\). Em hãy chọn câu trả lời đúng nhất.
-
A.
\(BC < AB < AC\)
-
B.
\(AC < AB < BC\)
-
C.
\(AC < BC < AB\)
-
D.
\(AB < BC < AC\)
Cho \(\Delta ABC\) có \(AC > BC > AB\). Trong các khẳng định sau, câu nào đúng?
-
A.
\(\widehat A > \widehat B > \widehat C\)
-
B.
\(\widehat C > \widehat A > \widehat B\)
-
C.
\(\widehat C < \widehat A < \widehat B\)
-
D.
\(\widehat A < \widehat B < \widehat C\)
Lời giải và đáp án
-
A.
\(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \)
-
B.
\(\widehat {CAD} + \widehat {BAD} + \widehat {BAC} = 180^\circ \)
-
C.
\(\widehat {CAD} + \widehat {ADC} + \widehat {ACB} = 180^\circ \)
-
D.
\(\widehat {BAC} + \widehat {ACD} + \widehat {ABD} = 180^\circ \)
Đáp án : B
Tổng số đo 3 góc trong 1 tam giác bằng 180 độ
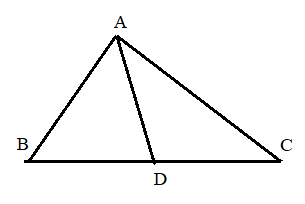
Áp dụng định lí tổng số đo 3 góc trong 3 tam giác ABD, ACD và ABC, ta được:
\(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \)
\(\widehat {CAD} + \widehat {ADC} + \widehat {ACB} = 180^\circ \)
\(\widehat {BAC} + \widehat {ACD} + \widehat {ABD} = 180^\circ \)
Vậy A,C,D đúng
Cho tam giác ABC có \(\widehat A = 86^\circ ;\widehat B = 62^\circ \). Số đo góc C là:
-
A.
\({32^0}\)
-
B.
\({35^0}\)
-
C.
\(24^\circ \)
-
D.
\({90^0}\)
Đáp án : A
Tổng số đo 3 góc trong 1 tam giác bằng 180 độ
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 86^\circ + 62^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ - 86^\circ - 62^\circ = 32^\circ \end{array}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({100^0}\)
Đáp án : B
Áp dụng tính chất tổng ba góc của một tam giác: Trong \(\Delta ABC:\,\widehat A + \widehat B + \widehat C = {180^0}.\)
Áp dụng tính chất tổng ba góc trong tam giác ABC, ta có:
\(\widehat A + \widehat B + \widehat C = {180^0}\)
Suy ra \(\widehat B + \widehat C = {180^0} - \widehat A = {180^0} - {80^0} = {100^0}\).
Hay \(x + x = {100^0}\) hay \( 2x = {100^0} \) suy ra \( x = {50^0}\)
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc C cắt cạnh AB tại M. Số đo góc BMC là:
-
A.
\({50^0}\)
-
B.
\(80^\circ \)
-
C.
\({100^0}\)
-
D.
\({90^0}\)
Đáp án : B
Áp dụng tính chất tổng ba góc của một tam giác, tính chất tia phân giác của một góc.
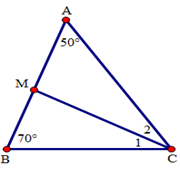
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat C = {180^0} - \left( {\widehat A + \widehat B} \right) = {180^0} - \left( {{{50}^0} + {{70}^0}} \right) = {60^0}\).
Do CM là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat C}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\).
Áp dụng định lí tổng ba góc trong tam giác BMC có:
\(\widehat B + \widehat {BMC} + {\widehat C_1} = {180^0} \Rightarrow \widehat {BMC} = {180^0} - \left( {\widehat B + \widehat {{C_1}}} \right) = {180^0} - \left( {{{70}^0} + {{30}^0}} \right) = {80^0}\)
Tam giác ABC có \(\widehat A = {80^0},\widehat B - \widehat C = {50^0}\). Số đo góc B và góc C lần lượt là:
-
A.
\(\widehat B = {65^0},\widehat C = {15^0}\)
-
B.
\(\widehat B = {75^0},\widehat C = {25^0}\)
-
C.
\(\widehat B = {70^0},\widehat C = {20^0}\)
-
D.
\(\widehat B = {80^0},\widehat C = {30^0}\)
Đáp án : B
+ Áp dụng tính chất tổng ba góc của một tam giác, tính tổng 2 góc B và C
+ Bài toán trở về tìm 2 số biết tổng và hiệu của chúng
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat B + \widehat C = 180^\circ - 80^\circ = 100^\circ \)
Ta có:
\(\begin{array}{l}\widehat C = (100^\circ - 50^\circ ):2 = 25^\circ ;\\\widehat B = \widehat C + 50^\circ = 25^\circ + 50^\circ = 75^\circ \end{array}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({70^0}\)
Đáp án : C
Áp dụng tính chất tổng ba góc của một tam giác
Áp dụng tính chất tổng ba góc trong tam giác ACF có :\(\widehat A + \widehat {ACF} + \widehat {AFC} = {180^0} \Leftrightarrow {60^0} + \widehat {ACF} + {90^0} = {180^0}\)
\( \Rightarrow \widehat {ACF} = {180^0} - {60^0} - {90^0} = {30^0}.\)
Áp dụng tính chất tổng ba góc trong \(\Delta IEC\) ta có: \(\widehat {IEC} + \widehat {ECI} + \widehat {EIC} = {180^0} \Leftrightarrow {30^0} + x + {90^0} = {180^0}\)
\( \Rightarrow x = {180^0} - {30^0} - {90^0} = {60^0}.\)
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác của các góc ACE và DBE cắt nhau ở K. Tính số đo góc BKC?
-
A.
90\(^\circ \)
-
B.
\(\widehat {BDC} - \widehat {BAC}\)
-
C.
\(\frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
-
D.
\(\widehat {BDC} + \widehat {BAC}\)
Đáp án : C
Áp dụng tính chất tổng ba góc của một tam giác
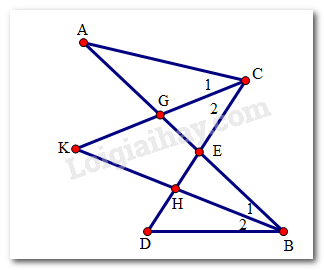
Gọi G là giao điểm của CK và AE, H là giao điểm của BK và DE.
Xét tam giác KGB và tam giác AGC và theo tính chất góc ngoài của tam giác ta có:\(\left\{ \begin{array}{l}\widehat K + \widehat {{B_1}} = \widehat {AGK}\\\widehat A + \widehat {{C_1}} = \widehat {AGK}\end{array} \right. \Rightarrow \widehat K + \widehat {{B_1}} = \widehat A + \widehat {{C_1}}\) (1)
Xét tam giác KHC và tam giác DHB và theo tính chất góc ngoài của tam giác ta có:\(\left\{ \begin{array}{l}\widehat K + \widehat {{C_2}} = \widehat {EHB}\\\widehat D + \widehat {{B_2}} = \widehat {EHB}\end{array} \right. \Rightarrow \widehat K + \widehat {{C_2}} = \widehat D + \widehat {{B_2}}\) (2)
Do \(\widehat {{B_1}} = \widehat {{B_2}}\) (BK là tia phân giác của góc DBA);
\(\widehat {{C_1}} = \widehat {{C_2}}\) ( CK là tia phân giác của góc ACD).
Nên cộng (1) với (2) ta được \(2\widehat K = \widehat A + \widehat D\), do đó \(\widehat K = \frac{{\widehat A + \widehat D}}{2}\) hay \(\widehat {BKC} = \frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
Tam giác ABC có \(\widehat B + \widehat C = \widehat A\) và \(\widehat C = 2\widehat B\). Tia phân giác của góc C cắt AB ở D. Tính \(\widehat {ADC}\)
-
A.
60\(^\circ \)
-
B.
90\(^\circ \)
-
C.
120\(^\circ \)
-
D.
30\(^\circ \)
Đáp án : A
Sử dụng tính chất tổng các góc của một tam giác, tính chất tia phân giác của một góc

Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = {180^0}\) mà \(\widehat B + \widehat C = \widehat A\), do đó \(2\widehat A = {180^0} \Rightarrow \widehat A = {90^0}\).
Trong tam giác ABC do \(\widehat A = {90^0}\) nên \(\widehat B + \widehat C = {90^ \circ }\). Mà \(\widehat C = 2\widehat B\) do đó \(3\widehat B = {90^0} \Rightarrow \widehat B = {30^0}\)nên \(\widehat C = {60^0}\)
Do CD là tia phân giác của góc ACD nên \(\widehat {ACD} = \widehat {DCB} = \widehat C:2 = {60^ \circ }:2 = {30^ \circ }\)
Xét tam giác ADC có: \(\widehat A + \widehat {ADC} + \widehat {ACD} = {180^0} \Rightarrow \widehat {ADC} = {180^0} - \left( {\widehat A + \widehat {ACD}} \right) = {180^0} - \left( {{{30}^0} + {{90}^ \circ }} \right) = {60^ \circ }\)
Khẳng định nào sau đây là sai?
-
A.
Tam giác tù là tam giác có 1 góc tù
-
B.
Tam giác nhọn là tam giác có 3 góc đều là góc nhọn
-
C.
Góc lớn nhất trong 1 tam giác là góc tù
-
D.
2 góc nhọn trong tam giác vuông phụ nhau.
Đáp án : C
Lý thuyết về 3 loại tam giác: Tam giác tù, tam giác vuông, tam giác nhọn
Các khẳng định A,B,D đúng.
Khẳng định C sai vì: Góc lớn nhất trong tam giác nhọn là một góc nhọn, góc lớn nhất trong tam giác vuông là góc vuông.
-
A.
\({90^0}\)
-
B.
\({100^0}\)
-
C.
\({120^0}\)
-
D.
\({130^0}\)
Đáp án : D
Góc ngoài tam giác bằng tổng 2 góc trong không kề với nó.
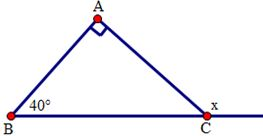
Ta có góc cần tính là góc ngoài tại đỉnh C của tam giác ABC nên:
\(x = \widehat A + \widehat B = 90^\circ + 40^\circ = 130^\circ \)
Cho tam giác \(ABH\) vuông tại \(H\,\left( {\widehat A > \widehat B} \right).\) Kẻ đường cao \(HC\,\,\left( {C \in AB} \right).\) So sánh \(BH\) và \(AH;\,CH\) và \(CB.\)
-
A.
\(BH > AH;\,\,CB < CH\)
-
B.
\(BH > AH;\,\,CB > CH\)
-
C.
\(BH < AH;\,\,CB < CH\)
-
D.
\(BH < AH;\,\,CB > CH\)
Đáp án : B
- Áp dụng:
+ Định lý: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
+ Định lý: Trong tam giác vuông, hai góc nhọn phụ nhau.

\(\Delta ABH\) có \(\widehat A > \widehat B\,\,(gt)\) nên \(BH > AH\) (quan hệ giữa góc và cạnh đối diện trong tam giác).
\(\Delta ABH\) vuông tại \(H\) nên \(\widehat A + \widehat B = {90^o}\) (1)
\(\Delta BCH\) vuông tại \(C\) nên \(\widehat {BHC} + \widehat B = {90^o}\) (2)
Từ (1) và (2) suy ra \(\widehat A = \widehat {BHC}\).
Mặt khác \(\widehat A > \widehat B\,\,(gt)\) nên \(\widehat {BHC} > \widehat B\) suy ra \(CB > CH\) (quan hệ giữa góc và cạnh đối diện trong tam giác).
Cho tam giác $ABC,$ biết \(\widehat A:\widehat B:\widehat C = 3:5:7.\) So sánh các cạnh của tam giác.
-
A.
\(AC < AB < BC\)
-
B.
\(BC > AC > AB\)
-
C.
\(BC < AC < AB\)
-
D.
\(BC = AC < AB\)
Đáp án : C
- Từ tỉ lệ góc cho trước ta so sánh các góc
- Sử dụng quan hệ giữa cạnh và góc trong tam giác để so sánh các cạnh.
Từ đề bài ta có \(\widehat A:\widehat B:\widehat C = 3:5:7\) nên \(\dfrac{{\widehat A}}{3} = \dfrac{{\widehat B}}{5} = \dfrac{{\widehat C}}{7}\)\( \Rightarrow \widehat A < \widehat B < \widehat C\)
Vì \(\widehat A < \widehat B < \widehat C\) nên \(BC < AC < AB.\)
\(\Delta ABH\) có \(\widehat A > \widehat B\,\,(gt)\) nên \(BH > AH\) (quan hệ giữa góc và cạnh đối diện trong tam giác).
\(\Delta ABH\) vuông tại \(H\) nên \(\widehat A + \widehat B = {90^o}\) (1)
\(\Delta BCH\) vuông tại \(C\) nên \(\widehat {BHC} + \widehat B = {90^o}\) (2)
Từ (1) và (2) suy ra \(\widehat A = \widehat {BHC}\).
Mặt khác \(\widehat A > \widehat B\,\,(gt)\) nên \(\widehat {BHC} > \widehat B\) suy ra \(CB > CH\) (quan hệ giữa góc và cạnh đối diện trong tam giác).
Cho tam giác $ABC$ cân ở $A$ có chu vi bằng $16cm,$ cạnh đáy $BC = 4cm.$ So sánh các góc của tam giác $ABC.$
-
A.
\(\widehat C = \widehat B > \widehat A\)
-
B.
\(\widehat A = \widehat B > \widehat C\)
-
C.
$\widehat C > \widehat B > \widehat A$
-
D.
\(\widehat C < \widehat B < \widehat A\)
Đáp án : A
- Tính độ dài các cạnh của tam giác
- Sử dụng quan hệ giữa cạnh và góc trong tam giác để so sánh các góc.
Vì tam giác \(ABC\) cân tại \(A\) nên \(AB = AC\)
Chu vi tam giác $ABC$ là \(16\,cm\) nên ta có \(AB + AC + BC = 16 \Rightarrow 2AB = 16 - BC\)\( \Rightarrow 2.AB = 16 - 4\)
\( \Rightarrow 2.AB = 12\)\( \Rightarrow AB = 6\,cm\) nên \(AB = AC > BC\)
Vì \(AB = AC > BC\) nên \(\widehat C = \widehat B > \widehat A.\)
Cho \(\Delta ABC\) cân tại $A.$ Trên $BC$ lấy hai điểm $D$ và $E$ sao cho \(BD = DE = EC\). Chọn câu đúng.
-
A.
\(\widehat {BAD} = \widehat {EAC}\)
-
B.
\(\widehat {EAC} < \widehat {DAE}\)
-
C.
\(\widehat {BAD} < \widehat {DAE}\)
-
D.
Cả A, B, C đều đúng.
Đáp án : D
Áp dụng hai định lý:
- Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
- Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
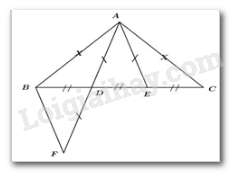
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
$AB = AC$ (gt)
\(\widehat B = \widehat C\) (tính chất tam giác cân)
\(BD = EC\left( {gt} \right)\)
\( \Rightarrow \Delta ABD = \Delta ACE\left( {c - g - c} \right)\)\( \Rightarrow \widehat {BAD} = \widehat {CAE}\) (2 góc tương ứng) nên A đúng.
Trên tia đối của tia $DA$ lấy điểm $F$ sao cho \(AD = DF\).
Xét \(\Delta ADE\) và \(\Delta FDB\) có:
\(AD = DF\left( {gt} \right)\)
\(\widehat {ADE} = \widehat {BDF}\) (đối đỉnh)
\(BD = DE\left( {gt} \right)\)
$ \Rightarrow \Delta ADE = \Delta FDB\left( {c - g - c} \right) \Rightarrow \left\{ \begin{array}{l}\widehat {DAE} = \widehat {BFD}\\AE = BF\end{array} \right.$
Ta có: \(\widehat {AEC} = \widehat B + \widehat {BAD}\) (tính chất góc ngoài của tam giác)
\( \Rightarrow \widehat {AEC} > \widehat B = \widehat C\) nên trong \(\Delta AEC\) suy ra \(AE < AC\) (quan hệ giữa góc và cạnh trong tam giác)
Mà \(\left\{ \begin{array}{l}AB = AC\left( {gt} \right)\\BF = AE\left( {cmt} \right)\end{array} \right. \Rightarrow BF < AB\)
Xét \(\Delta ABF\) có: \(BF < AB\left( {cmt} \right)\) suy ra \(\widehat {BFA} > \widehat {FAB}\) (quan hệ giữa cạnh và góc trong tam giác)
Vậy \(\widehat {BAD} = \widehat {CAE} < \widehat {DAE}\) nên B, C đúng.
Vậy cả A, B, C đều đúng.
Cho \(\Delta ABC\) có $AB > AC$ . Kẻ $BN$ là tia phân giác của góc $B$ \(\left( {N \in AC} \right)\). Kẻ $CM$ là tia phân giác của góc $C$\(\left( {M \in AB} \right)\), $CM$ và $BN$ cắt nhau tại $I.$ So sánh $IC$ và $IB?$
-
A.
\(IB < IC\)
-
B.
\(IC > IB\)
-
C.
\(IB = IC\)
-
D.
\(IB > IC\)
Đáp án : D
- Áp dụng tính chất tia phân giác của một góc.
- Chứng minh \(\widehat {MCB} > \widehat {NBC}\) .
- Áp dụng định lý: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Vì \(AB > AC \Rightarrow \widehat {ACB} > \widehat {ABC}\left( 1 \right)\) (quan hệ giữa cạnh và góc trong tam giác)
Vì $BN$ là phân giác của \(\widehat {ABC} \Rightarrow \widehat {NBC} = \dfrac{{\widehat {ABC}}}{2}\left( 2 \right)\) (tính chất phân giác)
Vì $CM$ là phân giác của \(\widehat {ACB} \Rightarrow \widehat {MCB} = \dfrac{{\widehat {ACB}}}{2}\left( 3 \right)\) (tính chất phân giác)
Từ \(\left( 1 \right)\left( 2 \right)\left( 3 \right)\) \(\Rightarrow \widehat {MCB} > \widehat {NBC}\,\,hay\,\,\,\widehat {ICB} > \widehat {IBC}.\)
Xét \(\Delta BIC\) có \(\widehat {MCB} > \widehat {NBC}\left( {cmt} \right) \Rightarrow IB > IC\) (quan hệ giữa góc và cạnh trong tam giác)
Cho \(\Delta ABC\) có \(AB < AC\) . Gọi $M$ là trung điểm của $BC.$ Trên tia đối của tia $MA$ lấy điểm $D$ sao cho $MA{\rm{ }} = {\rm{ }}MD$. So sánh \(\widehat {CDA}\) và \(\widehat {CAD}\) ?
-
A.
\(\widehat {CAD} > \widehat {CDA}\)
-
B.
\(\widehat {CAD} = \widehat {CDA}\)
-
C.
$\widehat {CAD} < \widehat {CDA}$
-
D.
\(\widehat {CDA} < \widehat {CAD}\)
Đáp án : C
- Chứng minh \(\Delta ABM = \Delta DCM\).
- Chứng minh \(DC < AC\).
- Áp dụng định lý: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Vì $M$ là trung điểm của $BC$ (gt) \( \Rightarrow MB = MC\) (tính chất trung điểm).
Ta có: \(\widehat {AMB} = \widehat {DMC}\) ($2$ góc đối đỉnh).
Xét \(\Delta ABM\) và \(\Delta DCM\)có:
\(\left\{ \begin{array}{l}AM = MD\left( {gt} \right)\\\widehat {AMB} = \widehat {DMC}\left( {cmt} \right)\\BM = MC\left( {cmt} \right)\end{array} \right.\)
\( \Rightarrow \Delta ABM = \Delta DCM\left( {c - g - c} \right)\)
\( \Rightarrow AB = DC\left( 1 \right)\) (2 cạnh tương ứng)
Lại có, \(AB < AC\left( {gt} \right)\left( 2 \right)\) . Từ \(\left( 1 \right)\) và \(\left( 2 \right) \Rightarrow DC < AC\).
Xét \(\Delta ADC\) có: \(DC < AC\left( {cmt} \right) \Rightarrow \widehat {CAD} < \widehat {CDA}\) (quan hệ giữa góc và cạnh đối diện trong tam giác)
Cho tam giác \(ABC\) có góc \(A\) tù. Trên cạnh \(AB\) lấy điểm \(E,\) trên cạnh \(AC\) lấy điểm \(F.\) Chọn câu đúng.
-
A.
\(BF > EF\)
-
B.
\(EF < BC\)
-
C.
\(BF < BC\)
-
D.
Cả A, B, C đều đúng
Đáp án : D
Sử dụng quan hệ giữa cạnh và góc trong tam giác.
Chú ý rằng: Trong tam giác tù thì cạnh đối diện với góc tù là cạnh lớn nhất trong tam giác.
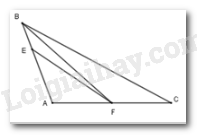
Do \(\widehat A > 90^\circ \Rightarrow \widehat {AEF} < 90^\circ \) (vì $\widehat A +\widehat {AEF}+\widehat {AFE}=180^0$)
\(\Rightarrow \widehat {BEF} > 90^\circ \) \( \Rightarrow BF > EF\,\,\left( 1 \right)\) nên A đúng
Do \(\widehat A > 90^\circ \Rightarrow \widehat {BFA} < 90^\circ \) (vì $\widehat A +\widehat {AEF}+\widehat {AFE}=180^0$)
\( \Rightarrow \widehat {BFC} > 90^\circ \) \( \Rightarrow BF < BC\,\left( 2 \right)\) nên C đúng
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(EF < BC\) nên B đúng.
Vậy cả A, B, C đều đúng.
Cho tam giác \(ABC\) có \(\widehat C > \widehat B\) (\(\widehat B,\,\widehat C\) là các góc nhọn). Vẽ phân giác \(AD.\) So sánh \(BD\) và \(CD.\)
-
A.
Chưa đủ điều kiện để so sánh
-
B.
\(BD = CD\)
-
C.
\(BD < CD\)
-
D.
\(BD > CD\)
Đáp án : D
+ Trên cạnh \(AB\) lấy điểm \(E\) sao cho \(AC = AE.\)
+ So sánh $CD$ với \(DE\) bằng cách sử dụng hai tam giác bằng nhau
+ So sánh $DE$ với \(BC\) theo quan hệ giữa cạnh và góc trong tam giác
+ Từ đó so sánh \(CD\) và \(BD.\)
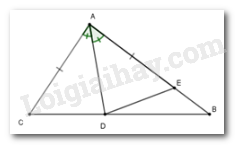
Từ đề bài \(\widehat C > \widehat B \Rightarrow AB > AC.\) Trên cạnh \(AB\) lấy điểm \(E\) sao cho \(AC = AE.\)
Xét tam giác \(ACD\) và tam giác \(AED\) có
+ \(AC = AE\)
+ \(\widehat {CAD} = \widehat {DAB}\) (tính chất tia phân giác)
+ Cạnh \(AD\) chung
Suy ra \(\Delta ACD = \Delta AED\left( {c - g - c} \right)\)
\( \Rightarrow DE = CD\,\,\left( 1 \right)\) và \(\widehat {AED} = \widehat {ACD}\)
Mà \(\widehat {ACD}\) là góc nhọn nên \(\widehat {AED}\) là góc nhọn, suy ra \(\widehat {BED} = 180^\circ - \widehat {AED}\) là góc tù, do đó \(\widehat {BED} > \widehat {EBD}\)
Xét tam giác \(BED\) có \(\widehat {BED} > \widehat {EBD}\) suy ra \(BD > DE\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(DC < BD.\)
Cho \(\Delta ABC\) có \(\widehat A = {70}\), \(\widehat B - \widehat C = {30^0}\) . Em hãy chọn câu trả lời đúng nhất:
-
A.
\(AC < AB < BC\)
-
B.
\(AB < AC = BC\)
-
C.
\(BC < AC = AB\)
-
D.
\(AC < BC < AB\)
Đáp án : B
- Tính số đo \(\widehat B\) và \(\widehat C\) của \(\Delta ABC\).
- Áp dụng định lý: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
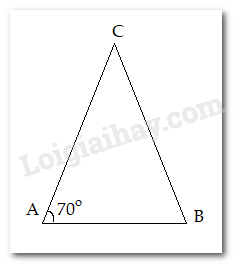
Xét \(\Delta ABC\) có $\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat B + \widehat C = {180^0} - \widehat A = {180^0} - {70^0} = {110^0}$
Ta có: $\left\{ \begin{array}{l}\widehat B + \widehat C = {110^0}\,\,\,\left( 1 \right)\\\widehat B - \widehat C = {30^0}\,\,\,\left( 2 \right)\end{array} \right.$
Từ \(\left( 2 \right) \Rightarrow \widehat C = \widehat B - {30^0}.\) Thế vào (1) ta được:
\(\widehat B + \widehat B - {30^0} = {110^0} \Rightarrow 2\widehat B = {140^0} \Rightarrow \widehat B = {70^0}\)
\( \Rightarrow \widehat C = {70^0} - {30^0} = {40^0}.\)
\( \Rightarrow \widehat C < \widehat B = \widehat A\)\( \Rightarrow AB < AC = BC.\) ( Định lí cạnh và góc đối diện trong tam giác)
Cho \(\Delta ABC\) có \(AB + AC = 10cm,AC - AB = 4cm\). So sánh \(\widehat B\) và \(\widehat C\)?
-
A.
\(\widehat C < \widehat B\)
-
B.
$\widehat C > \widehat B$
-
C.
\(\widehat C = \widehat B\)
-
D.
\(\widehat B < \widehat C\)
Đáp án : A
- Tính và so sánh độ dài các cạnh của tam giác.
- Áp dụng định lý: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
Xét \(\Delta ABC\) có: \(\left\{ \begin{array}{l}AB + AC = 10cm\,\,\,\left( 1 \right)\\AC - AB = 4cm\,\,\,\left( 2 \right)\end{array} \right.\)
$ \Rightarrow AC = 10 - AB$ . Thế vào (2) ta được: \(10 - AB - AB = 4 \Rightarrow 2AB = 6 \Rightarrow AB = 3\,cm.\)
\( \Rightarrow AC = 10 - 3 = 7\,cm.\)
\( \Rightarrow AC > AB \Rightarrow \widehat B > \widehat C.\)
Chọn câu trả lời đúng. Ba cạnh của tam giác có độ dài là \(6cm;\,7cm;\,8cm.\) Góc lớn nhất là góc
-
A.
đối diện với cạnh có độ dài \(6\,cm.\)
-
B.
đối diện với cạnh có độ dài \(7\,cm.\)
-
C.
đối diện với cạnh có độ dài \(8\,cm.\)
-
D.
Ba cạnh có độ dài bằng nhau.
Đáp án : C
- Áp dụng định lý: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
Vì trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn mà cạnh \(8\,cm\) là cạnh lớn nhất trong tam giác nên góc lớn nhất là góc đối diện với cạnh có độ dài \(8\,cm.\)
Cho tam giác $ABC$ có \(\widehat B = {90^0}\), \(\widehat A = {35^0}\). Em hãy chọn câu trả lời đúng nhất.
-
A.
\(BC < AB < AC\)
-
B.
\(AC < AB < BC\)
-
C.
\(AC < BC < AB\)
-
D.
\(AB < BC < AC\)
Đáp án : A
- Tính \(\widehat C\) và so sánh các góc của\(\Delta ABC\).
- Áp dụng định lý: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
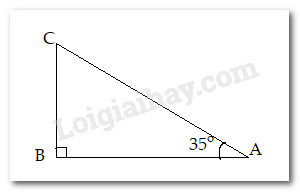
Xét \(\Delta ABC\) có:
\(\widehat A + \widehat B + \widehat C = {180^0}\) (định lý tổng ba góc trong tam giác)
\( \Rightarrow \widehat C = {180^0} - \widehat A - \widehat B = {180^0} - {35^0} - {90^0} = {55^0}\)
\( \Rightarrow \widehat A < \widehat C < \widehat B \Rightarrow BC < AB < AC\)
Cho \(\Delta ABC\) có \(AC > BC > AB\). Trong các khẳng định sau, câu nào đúng?
-
A.
\(\widehat A > \widehat B > \widehat C\)
-
B.
\(\widehat C > \widehat A > \widehat B\)
-
C.
\(\widehat C < \widehat A < \widehat B\)
-
D.
\(\widehat A < \widehat B < \widehat C\)
Đáp án : C
Áp dụng định lý: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
Vì \(\Delta ABC\) có \(AC > BC > AB\) nên theo quan hệ giữa cạnh và góc trong tam giác ta có \(\widehat B > \widehat A > \widehat C\) hay \(\widehat C < \widehat A < \widehat B\).