Trắc nghiệm Bài 7: Trường hợp đồng dạng thứ hai của tam giác Toán 8 Cánh diều
Đề bài
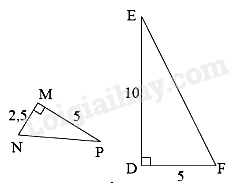
Cho tam giác ABC vuông tại A có: \(AB = 3cm,AC = 5cm\) và tam giác MNP vuông tại M có \(MN = 12cm,MP = 20cm.\) Khi đó,
-
A.
\(\Delta ABC = \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta MNP\)
-
C.
\(\Delta BAC \backsim \Delta MNP\)
-
D.
\(\Delta BCA \backsim \Delta MNP\)
-
A.
\(\Delta MNP \backsim \Delta DFE\)
-
B.
\(\Delta MNP \backsim \Delta DEF\)
-
C.
\(\Delta MNP = \Delta DFE\)
-
D.
Cả A, B, C đều sai
Hai tam giác vuông đồng dạng với nhau khi:
-
A.
Hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác kia
-
B.
Hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác kia
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}}\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
-
A.
\(\widehat B = \widehat D\)
-
B.
\(\widehat B = \frac{2}{3}\widehat D\)
-
C.
\(\frac{2}{3}\widehat B = \widehat D\)
-
D.
\(\widehat B = \frac{3}{4}\widehat D\)
-
A.
\(\widehat {ABC} + \widehat {EBD} = {80^0}\)
-
B.
\(\widehat {ABC} + \widehat {EBD} = {85^0}\)
-
C.
\(\widehat {ABC} + \widehat {EBD} = {95^0}\)
-
D.
\(\widehat {ABC} + \widehat {EBD} = {90^0}\)
-
A.
\(\widehat {BAH} = \widehat C\)
-
B.
\(\widehat {BAH} = \frac{2}{3}\widehat C\)
-
C.
\(\frac{2}{3}\widehat {BAH} = \widehat C\)
-
D.
Cả A, B, C đều sai
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}.\) Gọi M, M’ lần lượt là trung điểm của BC và B’C’. Khi đó, tỉ số \(\frac{{AM}}{{A'M'}}\) bằng
-
A.
\(\frac{1}{3}\)
-
B.
\(\frac{1}{4}\)
-
C.
\(\frac{1}{2}\)
-
D.
\(2\)
Trên đoạn \(BC = 13cm,\) đặt đoạn \(BH = 4cm.\) Trên đường vuông góc với BC tại H, lấy điểm A sao cho \(HA = 6cm\)
Cho các khẳng định sau:
1. Số đo góc BAC bằng 80 độ
2. \(AB.AC = AH.BC\)
3. \(\widehat B > \widehat {CAH}\)
Có bao nhiêu khẳng định đúng?
-
A.
0
-
B.
1
-
C.
3
-
D.
2
Cho hình thang ABCD vuông tại A và D. Biết \(CD = 2AB = 2AD = 2a\) và \(BC = a\sqrt 2 .\) Gọi I là trung điểm của BC, H là chân đường vuông góc kẻ từ D xuống AC. Khi đó:
-
A.
\(\widehat {HDI} = {45^0}\)
-
B.
\(\widehat {HDI} = {40^0}\)
-
C.
\(\widehat {HDI} = {50^0}\)
-
D.
\(\widehat {HDI} = {55^0}\)
Cho O là trung điểm của đoạn AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm C (khác A), qua O kẻ đường thẳng vuông góc với OC cắt tia By tại D. Kẻ OM vuông góc với CD tại M. Khi đó:
-
A.
\(AC = \frac{4}{3}MC\)
-
B.
\(AC = \frac{3}{2}MC\)
-
C.
\(AC = \frac{2}{3}MC\)
-
D.
\(AC = MC\)
Cho tam giác ABC vuông tại A có M là trung điểm của BC. Gọi I là hình chiếu của M trên AC. Chọn đáp án đúng.
-
A.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{2}\)
-
B.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{3}\)
-
C.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{4}\)
-
D.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{2}{3}\)
-
A.
\(CE = \sqrt {66} \)
-
B.
\(CE = \sqrt {65} \)
-
C.
\(CE = 8\)
-
D.
\(CE = 8,5\)
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’ có chu vi bằng 30cm, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}} = \frac{3}{2}\). Chu vi tam giác ABC là:
-
A.
15cm
-
B.
20cm
-
C.
30cm
-
D.
45cm
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}}\). Biết rằng \(\widehat {A'B'C'} = \frac{1}{7}\widehat {BAC}.\) Chọn đáp án đúng
-
A.
\(\widehat {BAC} = {140^0}\)
-
B.
\(\widehat {BAC} = {100^0}\)
-
C.
\(\widehat {BAC} = {120^0}\)
-
D.
\(\widehat {BAC} = {110^0}\)
Cho hình thang vuông ABCD, \(\left( {\widehat A = \widehat D = {{90}^0}} \right)\) có \(AB = 4cm,CD = 9cm\) và \(BC = 13cm.\) Khoảng cách từ M đến BC bằng:
-
A.
4cm
-
B.
5cm
-
C.
6cm
-
D.
7cm
Cho tam giác ABC vuông tại A, \(AC = 3AB = 3a.\) Lấy các điểm D, E thuộc AC sao cho \(AD = DE = EC.\) Khi đó,
-
A.
\(\widehat {AEB} + \widehat {ACB} = {40^0}\)
-
B.
\(\widehat {AEB} + \widehat {ACB} = {45^0}\)
-
C.
\(\widehat {AEB} + \widehat {ACB} = {50^0}\)
-
D.
\(\widehat {AEB} + \widehat {ACB} = {55^0}\)
Hai tam giác đồng dạng với nhau theo trường hợp cạnh – góc – cạnh nếu
-
A.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
một cạnh của tam giác này bằng một cạnh của tam giác kia và một cặp góc bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Cho \(\Delta D{\rm{EF}}\) và \(\Delta ILK\) , biết DE = 10cm ; EF = 4cm ; IL = 20cm ; LK = 8cm cần thêm điều kiện gì để \(\Delta D{\rm{EF}} \backsim \Delta {\rm{ILK(c - g - c)?}}\)
-
A.
\(\hat E = \hat I.\)
-
B.
\(\hat E = \hat L\)
-
C.
\(\hat P = \hat I.\)
-
D.
\(\hat F = \hat K\)
-
A.
Hình 1 và hình 2.
-
B.
Hình 2 và hình 3.
-
C.
Hình 1 và hình 3.
-
D.
Hình 1, hình 2 và hình 3.
-
A.
\({50^0}\)
-
B.
\({60^0}\)
-
C.
\({30^0}\)
-
D.
\({70^0}\)
Cho \(\Delta {A'}{B'}{C'}\) và \(\Delta ABC\) có \(\hat A = {\hat A'}\) . Để \(\Delta {A'}{B}{C'} \backsim \Delta ABC\) cần thêm điều kiện là:
-
A.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{A'}{C'}}}{{AC}}.\)
-
B.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{B'}{C'}}}{{BC}}.\)
-
C.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{BC}}{{{B'}{C'}}}.\)
-
D.
\(\frac{{{B'}{C'}}}{{BC}} = \frac{{AC}}{{{A'}{C'}}}.\)
Cho \(\Delta MNP \backsim \Delta KIH\) , biết \(\hat M = \hat K,MN = 2cm,MP = 8cm,KH = 4cm\) , thì KI bằng bao nhiêu:
-
A.
\(KI = 2cm.\)
-
B.
\(KI = 6cm.\)
-
C.
\(KI = 4cm.\)
-
D.
\(KI = 1cm.\)
Cho \(\Delta ABC\) , lấy hai điểm D và E lần lượt nằm bên cạnh AB và AC sao cho \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\) Kết luận nào sau đây sai:
-
A.
\(\Delta ADE \backsim \Delta ABC.\)
-
B.
\(DE//BC.\)
-
C.
\(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}.\)
-
D.
\(\widehat {ADE} = \widehat {ABC.}\)
Cho \(\Delta ABC\) , có AC = 18cm; AB = 9cm; BC = 15cm . Trên cạnh AC lấy điểm N sao cho AN = 3cm , trên cạnh AB lấy điểm M sao cho AM = 6cm . Tính độ dài đoạn thẳng MN:
-
A.
MN= 6cm
-
B.
MN = 5cm
-
C.
MN = 8cm
-
D.
MN = 9cm
-
A.
x = 15
-
B.
x = 16
-
C.
x = 7
-
D.
x = 8
Cho \(\Delta ABC\) vuông tại A, đường cao \(AH(H \in BC)\) . Biết AB = 3cm, AC = 6cm,
AH = 2cm, HC = 4cm. Hệ thức nào sau đây đúng:
-
A.
\(A{C^2} = CH.BH\)
-
B.
\(AB.AH = HC.AC\)
-
C.
\(AB.HC = AH.AC\)
-
D.
\(AB.AC = AH.HC\)
Cho hình thang vuông \(ABCD(\hat A = \hat D = {90^0})\) có AB = 16cm, CD = 25cm,
BD = 20cm . Độ dài cạnh BC là:
-
A.
10 cm
-
B.
12cm
-
C.
15cm
-
D.
9cm
Cho \(\Delta MNP \backsim \Delta EFH\) theo tỉ số k. Gọi \(M{M'},E{E'}\) lần lượt là hai trung tuyến của \(\Delta MNP\) và \(\Delta EFH\) . Khi đó ta chứng minh được:
-
A.
\(\frac{{E{E'}}}{{M{M'}}} = k\)
-
B.
\(\frac{{M{M '}}}{{E{E '}}} = k\)
-
C.
\(\frac{{M{M '}}}{{E{E '}}} = {k^2}\)
-
D.
\(\frac{{E{E '}}}{{M{M '}}} = {k^2}\)
Cho tam giác nhọn ABC có \(\hat C = {60^0}\) . Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của tam giác ABC, ACD. Tính số đo góc AKH.
-
A.
\({30^0}\)
-
B.
\({60^0}\)
-
C.
\({45^0}\)
-
D.
\({50^0}\)
Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm . Hỏi góc B bằng bao nhiêu lần góc A?
-
A.
\(\hat B = \frac{{\hat A}}{3}\)
-
B.
\(\hat B = \frac{2}{3}\hat A\)
-
C.
\(\hat B = \frac{{\hat A}}{2}\)
-
D.
\(\hat B = \hat A\)
Cho hình thoi ABCD cạnh a, có \(\hat A = {60^0}\) . Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính \(\widehat {BKD}\) .
-
A.
\(\widehat {BKD} = {60^0}\)
-
B.
\(\widehat {BKD} = {100^0}\)
-
C.
\(\widehat {BKD} = {120^0}\)
-
D.
\(\widehat {BKD} = {115^0}\)
Cho hình thang vuông ABCD \(\left( {\hat A = \hat D = {{90}^0}} \right)\) có AB = 4cm, CD = 9cm, BC = 13cm . Gọi M là trung điểm của AD. Tính \(\widehat {BMC}\) .
-
A.
\({60^0}\)
-
B.
\({110^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Lời giải và đáp án
Cho tam giác ABC vuông tại A có: \(AB = 3cm,AC = 5cm\) và tam giác MNP vuông tại M có \(MN = 12cm,MP = 20cm.\) Khi đó,
-
A.
\(\Delta ABC = \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta MNP\)
-
C.
\(\Delta BAC \backsim \Delta MNP\)
-
D.
\(\Delta BCA \backsim \Delta MNP\)
Đáp án : B
Do đó, \(\Delta ABC \backsim \Delta MNP\)
-
A.
\(\Delta MNP \backsim \Delta DFE\)
-
B.
\(\Delta MNP \backsim \Delta DEF\)
-
C.
\(\Delta MNP = \Delta DFE\)
-
D.
Cả A, B, C đều sai
Đáp án : A
Tam giác MNP và tam giác DFE có: \(\widehat M = \widehat D = {90^0},\frac{{MN}}{{DF}} = \frac{{MP}}{{DE}}\left( { = \frac{1}{2}} \right)\) nên \(\Delta MNP \backsim \Delta DFE\)
Hai tam giác vuông đồng dạng với nhau khi:
-
A.
Hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác kia
-
B.
Hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác kia
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
Đáp án : C
Hai cạnh góc vuông của tam giác này lần lượt bằng hai cạnh góc vuông của tam giác kia thì khi đó tỉ lệ của hai cạnh tam giác vuông bằng 1. Do đó, hai tam giác cũng đồng dạng với nhau.
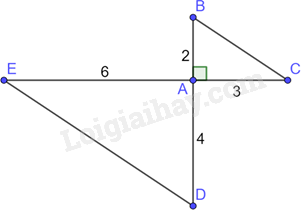
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}}\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
Đáp án : D
Tam giác ABC và tam giác DEF có: \(\widehat {BAC} = \widehat {EDF} = {90^0},\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}}\) nên \(\Delta ABC \backsim \Delta DEF\)
-
A.
\(\widehat B = \widehat D\)
-
B.
\(\widehat B = \frac{2}{3}\widehat D\)
-
C.
\(\frac{2}{3}\widehat B = \widehat D\)
-
D.
\(\widehat B = \frac{3}{4}\widehat D\)
Đáp án : A
Xét tam giác ABC và tam giác ADE có: \(\widehat {BAC} = \widehat {DAE} = {90^0}\), \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}}\left( { = \frac{1}{2}} \right)\)
Do đó, \(\Delta ABC \backsim \Delta ADE\)
Do đó, \(\widehat B = \widehat D\)
-
A.
\(\widehat {ABC} + \widehat {EBD} = {80^0}\)
-
B.
\(\widehat {ABC} + \widehat {EBD} = {85^0}\)
-
C.
\(\widehat {ABC} + \widehat {EBD} = {95^0}\)
-
D.
\(\widehat {ABC} + \widehat {EBD} = {90^0}\)
Đáp án : D
Ta có: \(\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\frac{{AC}}{{BD}} = \frac{3}{6} = \frac{1}{2}\) nên \(\frac{{AB}}{{DE}} = \frac{{AC}}{{BD}}\)
Tam giác ABC và tam giác DEB có: \(\widehat {BAC} = \widehat {BDE} = {90^0},\frac{{AB}}{{DE}} = \frac{{AC}}{{BD}}\) nên
Do đó, \(\widehat {CBA} = \widehat {BED}\)
Mà \(\widehat {BED} + \widehat {EBD} = {90^0}\) nên \(\widehat {ABC} + \widehat {EBD} = {90^0}\)
-
A.
\(\widehat {BAH} = \widehat C\)
-
B.
\(\widehat {BAH} = \frac{2}{3}\widehat C\)
-
C.
\(\frac{2}{3}\widehat {BAH} = \widehat C\)
-
D.
Cả A, B, C đều sai
Đáp án : A
Tam giác AHB và tam giác CAH có:\(\widehat {AHB} = \widehat {AHC} = {90^0},\frac{{BH}}{{AH}} = \frac{{AH}}{{HC}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta AHB \backsim \Delta CAH\)
Suy ra: \(\widehat {BAH} = \widehat C\)
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}.\) Gọi M, M’ lần lượt là trung điểm của BC và B’C’. Khi đó, tỉ số \(\frac{{AM}}{{A'M'}}\) bằng
-
A.
\(\frac{1}{3}\)
-
B.
\(\frac{1}{4}\)
-
C.
\(\frac{1}{2}\)
-
D.
\(2\)
Đáp án : C
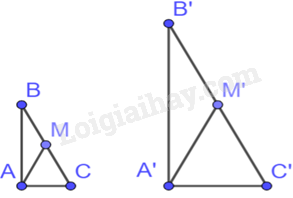
Tam giác ABC và tam giác A’B’C có: \(\widehat {BAC} = \widehat {B'A'C'} = {90^0},\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\)
Do đó, \(\Delta ABC \backsim \Delta A'B'C'\)
Suy ra: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\)
Mà M là trung điểm của BC nên \(BC = 2AM\), M’ là trung điểm của B’C’ nên \(B'C' = 2A'M'\)
Do đó, \(\frac{{AM}}{{A'M'}} = \frac{1}{2}\)
Trên đoạn \(BC = 13cm,\) đặt đoạn \(BH = 4cm.\) Trên đường vuông góc với BC tại H, lấy điểm A sao cho \(HA = 6cm\)
Cho các khẳng định sau:
1. Số đo góc BAC bằng 80 độ
2. \(AB.AC = AH.BC\)
3. \(\widehat B > \widehat {CAH}\)
Có bao nhiêu khẳng định đúng?
-
A.
0
-
B.
1
-
C.
3
-
D.
2
Đáp án : B
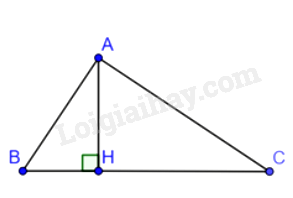
Ta có: \(HC = BC - BH = 9\left( {cm} \right)\)
Tam giác AHB và tam giác CAH có:
\(\widehat {AHB} = \widehat {AHC} = {90^0},\frac{{BH}}{{AH}} = \frac{{AH}}{{HC}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta AHB \backsim \Delta CAH\)
Suy ra: \(\widehat B = \widehat {CAH}\) (khẳng định (3) sai)
Mà \(\widehat B + \widehat {BAH} = {90^0}\) nên \(\widehat {BAH} + \widehat {CAH} = {90^0}\) hay \(\widehat {BAC} = {90^0}\) (khẳng định (1) sai)
Do đó, tam giác ABC vuông tại A.
Diện tích tam giác ABC là: \(\frac{1}{2}AB.AC = \frac{1}{2}AH.BC \Rightarrow AB.AC = AH.BC\) (khẳng định (2) đúng)
Vậy có 1 khẳng định đúng
Cho hình thang ABCD vuông tại A và D. Biết \(CD = 2AB = 2AD = 2a\) và \(BC = a\sqrt 2 .\) Gọi I là trung điểm của BC, H là chân đường vuông góc kẻ từ D xuống AC. Khi đó:
-
A.
\(\widehat {HDI} = {45^0}\)
-
B.
\(\widehat {HDI} = {40^0}\)
-
C.
\(\widehat {HDI} = {50^0}\)
-
D.
\(\widehat {HDI} = {55^0}\)
Đáp án : A
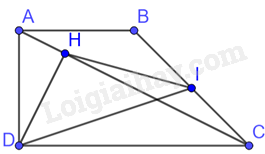
Áp dụng định lý Pythagore vào tam giác ADB vuông tại A có: \(B{D^2} = A{D^2} + A{B^2} = {a^2} + {a^2} = 2{a^2} \Rightarrow BD = a\sqrt 2 \)
Tam giác ABD vuông cân tại A nên \(\widehat {ADB} = {45^0}\)
Ta có: \(B{D^2} + B{C^2} = 2{a^2} + 2{a^2} = 4{a^2} = C{D^2}\) nên tam giác BDC vuông tại B, do đó, \(\widehat {DBC} = {90^0}\)
Xét tam giác ADC và tam giác IBD có:
\(\widehat {ADC} = \widehat {IBD} = {90^0},\frac{{AD}}{{IB}} = \frac{{DC}}{{BD}}\)
Do đó, \(\Delta ADC \backsim \Delta IBD\)
Suy ra, \(\widehat {ACD} = \widehat {BDI}\)
Mà \(\widehat {ADH} = \widehat {ACD}\) (cùng phụ với góc HDC)
Do đó, \(\widehat {ADH} = \widehat {BDI}\)
Mà \(\widehat {ADH} + \widehat {BDH} = {45^0} \Rightarrow \widehat {BDI} + \widehat {BDH} = {45^0}\) hay \(\widehat {HDI} = {45^0}\)
Cho O là trung điểm của đoạn AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm C (khác A), qua O kẻ đường thẳng vuông góc với OC cắt tia By tại D. Kẻ OM vuông góc với CD tại M. Khi đó:
-
A.
\(AC = \frac{4}{3}MC\)
-
B.
\(AC = \frac{3}{2}MC\)
-
C.
\(AC = \frac{2}{3}MC\)
-
D.
\(AC = MC\)
Đáp án : D
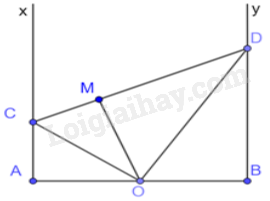
Tam giác OAC và tam giác DBO có: \(\widehat {OAC} = \widehat {DBO} = {90^0},\widehat {COA} = \widehat {BDO}\) (cùng phụ với góc DOB)
Do đó, \(\Delta OAC \backsim \Delta DBO \Rightarrow \frac{{OC}}{{OD}} = \frac{{AC}}{{OB}}\)
Mà \(OA = OB \Rightarrow \frac{{OC}}{{OD}} = \frac{{AC}}{{OA}} \Rightarrow \frac{{OC}}{{AC}} = \frac{{OD}}{{OA}}\)
Tam giác OCD và tam giác ACO có: \(\widehat {CAO} = \widehat {COD} = {90^0},\frac{{OC}}{{AC}} = \frac{{OD}}{{OA}}\)
Do đó, \(\Delta OCD \backsim \Delta ACO \Rightarrow \widehat {OCD} = \widehat {ACO}\)
Chứng minh được \(\Delta OAC = \Delta OMC\left( {ch - gn} \right) \Rightarrow AC = MC\)
Cho tam giác ABC vuông tại A có M là trung điểm của BC. Gọi I là hình chiếu của M trên AC. Chọn đáp án đúng.
-
A.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{2}\)
-
B.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{3}\)
-
C.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{4}\)
-
D.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{2}{3}\)
Đáp án : C
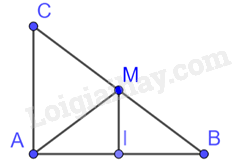
Tam giác ABC vuông tại A có AM là trung tuyến nên \(AM = MB = \frac{1}{2}BC\)
Do đó, tam giác AMB cân tại M. Do đó, MI là đường cao đồng thời là đường trung tuyến nên \(AI = \frac{1}{2}AB \Rightarrow \frac{{AI}}{{AB}} = \frac{1}{2}\)
Tam giác ABC có: M là trung điểm của CB, I là trung điểm của AB nên MI là đường trung bình của tam giác ABC nên \(\frac{{MI}}{{AC}} = \frac{1}{2}\)
Tam giác ABC và tam giác AIM có:
\(\widehat {BAC} = \widehat {MIA} = {90^0},\frac{{AI}}{{AB}} = \frac{{MI}}{{AC}}\left( { = \frac{1}{2}} \right)\) nên \(\Delta IAM \backsim \Delta ABC\)
Do đó, \(\frac{{{S_{ABC}}}}{{{S_{AMI}}}} = {\left( {\frac{{MI}}{{AC}}} \right)^2} = \frac{1}{4}\)
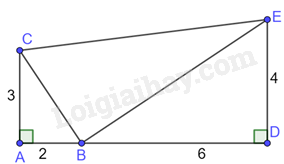
-
A.
\(CE = \sqrt {66} \)
-
B.
\(CE = \sqrt {65} \)
-
C.
\(CE = 8\)
-
D.
\(CE = 8,5\)
Đáp án : B
Ta có: \(\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\frac{{AC}}{{BD}} = \frac{3}{6} = \frac{1}{2}\) nên \(\frac{{AB}}{{DE}} = \frac{{AC}}{{BD}}\)
Tam giác ABC và tam giác DEB có: \(\widehat {BAC} = \widehat {BDE} = {90^0},\frac{{AB}}{{DE}} = \frac{{AC}}{{BD}}\) nên \(\Delta ABC \backsim \Delta DEB\)
Do đó, \(\widehat {CBA} = \widehat {BED}\)
Mà \(\widehat {BED} + \widehat {EBD} = {90^0}\) nên \(\widehat {ABC} + \widehat {EBD} = {90^0}\)
Mà \(\widehat {ABC} + \widehat {EBD} + \widehat {CBE} = {180^0}\) nên \(\widehat {CBE} = {90^0}\)
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có: \(B{C^2} = A{B^2} + A{C^2} = 13\)
Áp dụng định lý Pythagore vào tam giác BDE vuông tại D có: \(B{E^2} = D{E^2} + B{D^2} = 52\)
Áp dụng định lý Pythagore vào tam giác BCE vuông tại B có: \(C{E^2} = B{E^2} + B{C^2} = 65\) nên \(CE = \sqrt {65} \)
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’ có chu vi bằng 30cm, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}} = \frac{3}{2}\). Chu vi tam giác ABC là:
-
A.
15cm
-
B.
20cm
-
C.
30cm
-
D.
45cm
Đáp án : D
Tam giác BHC và tam giác B’H’C’ có: \(\widehat {BHC} = \widehat {B'H'C'} = {90^0},\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}} = \frac{3}{2}\)
Do đó, \(\Delta BHC \backsim \Delta B'H'C'\)
Suy ra: + \(\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}} = \frac{{BC}}{{B'C'}} = \frac{3}{2}\)
+ \(\widehat C = \widehat {C'}\), mà tam giác ABC cân tại A, tam giác A’B’C’ cân tại A’ nên \(\widehat B = \widehat {B'} = \widehat C = \widehat {C'}\)
Do đó, \(\Delta ABC \backsim \Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{3}{2}\)
Theo tính chất dãy tỉ số bằng nhau ta có: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{{AB + BC + AC}}{{A'B' + B'C' + A'C'}} = \frac{3}{2}\)
Mà chu vi tam giác A’B’C’ bằng 30cm nên chu vi tam giác ABC là: \(30.\frac{3}{2} = 45\left( {cm} \right)\)
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}}\). Biết rằng \(\widehat {A'B'C'} = \frac{1}{7}\widehat {BAC}.\) Chọn đáp án đúng
-
A.
\(\widehat {BAC} = {140^0}\)
-
B.
\(\widehat {BAC} = {100^0}\)
-
C.
\(\widehat {BAC} = {120^0}\)
-
D.
\(\widehat {BAC} = {110^0}\)
Đáp án : A
Tam giác BHC và tam giác B’H’C’ có: \(\widehat {BHC} = \widehat {B'H'C'} = {90^0},\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}}\)
Do đó, \(\Delta BHC \backsim \Delta B'H'C'\)
Suy ra: \(\widehat C = \widehat {C'}\), mà tam giác ABC cân tại A, tam giác A’B’C’ cân tại A’ nên \(\widehat B = \widehat {B'} = \widehat C = \widehat {C'}\)
Do đó, \(\widehat {BAC} = 7\widehat {ACB} = 7\widehat {ABC}\)
Lại có: \(\widehat {BAC} + \widehat {ACB} + \widehat {ABC} = {180^0} \Rightarrow 9\widehat {ACB} = {180^0} \Rightarrow \widehat {ACB} = {20^0} \Rightarrow \widehat {BAC} = {140^0}\)
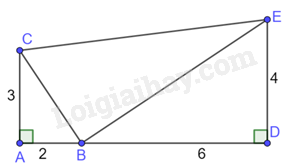
Cho hình thang vuông ABCD, \(\left( {\widehat A = \widehat D = {{90}^0}} \right)\) có \(AB = 4cm,CD = 9cm\) và \(BC = 13cm.\) Khoảng cách từ M đến BC bằng:
-
A.
4cm
-
B.
5cm
-
C.
6cm
-
D.
7cm
Đáp án : C
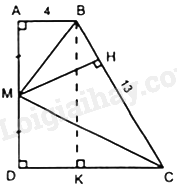
Kẻ BK vuông góc với CD tại K.
Tứ giác ABKD có: \(\widehat A = \widehat D = \widehat {BKD} = {90^0}\) nên tứ giác ABKD là hình chữ nhật, do đó, \(KC = DC - DK = 5cm\)
Áp dụng định lý Pythagore vào tam giác BKC vuông tại K ta có:
\(B{C^2} = C{K^2} + K{B^2} \Rightarrow K{B^2} = 144 \Rightarrow KB = 12cm\)
Vì tứ giác ABKD là hình chữ nhật nên \(AD = BK = 12cm\) do đó \(AM = MD = 6cm\)
Xét tam giác ABM và tam giác DMC có:
\(\widehat {BAM} = \widehat {MDC} = {90^0},\frac{{AB}}{{DM}} = \frac{{AM}}{{DC}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta ABM \backsim \Delta DMC\)
Suy ra, \(\widehat {AMB} = \widehat {DCM}\)
Mà \(\widehat {DMC} + \widehat {MCD} = {90^0} \Rightarrow \widehat {DMC} + \widehat {AMB} = {90^0}\)
Ta có: \(\widehat {DMC} + \widehat {BMC} + \widehat {AMB} = {180^0} \Rightarrow \widehat {BMC} = {90^0}\)
Do đó, tam giác BMC vuông tại M.
Kẻ MH vuông góc với BC tại H thì MH là khoảng cách từ M đến BC.
Áp dụng định lý Pythagore vào hai tam giác ABM và tam giác DMC ta được:
\(\left\{ \begin{array}{l}B{M^2} = M{A^2} + A{B^2} = {6^2} + {4^2} = 52\\M{C^2} = C{D^2} + D{M^2} = {9^2} + {6^2} = 117\end{array} \right.\)
Do đó, \(BM = 2\sqrt {13} cm,MC = 3\sqrt {13} cm\)
Diện tích tam giác BMC vuông tại M có:
\(\frac{1}{2}BM.MC = \frac{1}{2}MH.BC \Rightarrow 2\sqrt {13} .3\sqrt {13} = 13.MH \Rightarrow MH = 6cm\)
Cho tam giác ABC vuông tại A, \(AC = 3AB = 3a.\) Lấy các điểm D, E thuộc AC sao cho \(AD = DE = EC.\) Khi đó,
-
A.
\(\widehat {AEB} + \widehat {ACB} = {40^0}\)
-
B.
\(\widehat {AEB} + \widehat {ACB} = {45^0}\)
-
C.
\(\widehat {AEB} + \widehat {ACB} = {50^0}\)
-
D.
\(\widehat {AEB} + \widehat {ACB} = {55^0}\)
Đáp án : B

Ta có: \(AD = DE = EC = a\)
Vẽ M đối xứng với B qua D.
Tam giác BAD vuông tại A có \(AB = AD\) nên tam giác ABD vuông cân tại A. Suy ra: \(\widehat {ABD} = \widehat {ADB} = {45^0}\)
Chứng minh được \(\Delta ABD = \Delta EMD\) nên \(\widehat {ABD} = \widehat {EMD} = {45^0},\widehat {MED} = \widehat {BAD} = {90^0}\) và \(BD = DM = \frac{1}{2}BM,\;ME = AB = a\)
Tam giác MEC có ME là đường cao đồng thời là đường trung tuyến nên tam giác DME cân tại M. Do đó, ME là đường phân giác. Do đó, \(\widehat {DMC} = 2\widehat {DME} = {90^0}\)
Áp dụng định lý Pythagore vào tam giác ABD vuông tại A có: \(BD = a\sqrt 2 \Rightarrow BM = 2a\sqrt 2 \)
Áp dụng định lý Pythagore vào tam giác MEC vuông tại E có: \(MC = a\sqrt 2 \)
Ta có: \(\frac{{AB}}{{MC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }};\frac{{AE}}{{BM}} = \frac{{2a}}{{2a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} \Rightarrow \frac{{AB}}{{MC}} = \frac{{AE}}{{BM}}\)
Tam giác EAB và tam giác BMC có:
\(\widehat {BAE} = \widehat {BMC} = {90^0},\)\(\frac{{AB}}{{MC}} = \frac{{AE}}{{BM}}\) nên \(\Delta EAB \backsim \Delta BMC\)
Do đó, \(\widehat {BEA} = \widehat {MBC}\)
Mà \(\widehat {BEA} + \widehat {BCA} = \widehat {MBC} + \widehat {BCA} = \widehat {BDA} = {45^0}\)
Hai tam giác đồng dạng với nhau theo trường hợp cạnh – góc – cạnh nếu
-
A.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
một cạnh của tam giác này bằng một cạnh của tam giác kia và một cặp góc bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Đáp án : D
Hai tam giác đồng dạng với nhau theo trường hợp cạnh - góc – cạnh nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Cho \(\Delta D{\rm{EF}}\) và \(\Delta ILK\) , biết DE = 10cm ; EF = 4cm ; IL = 20cm ; LK = 8cm cần thêm điều kiện gì để \(\Delta D{\rm{EF}} \backsim \Delta {\rm{ILK(c - g - c)?}}\)
-
A.
\(\hat E = \hat I.\)
-
B.
\(\hat E = \hat L\)
-
C.
\(\hat P = \hat I.\)
-
D.
\(\hat F = \hat K\)
Đáp án : B
Ta có: \(\frac{{DE}}{{IL}} = \frac{{EF}}{{LK}}\left( {\frac{{10}}{{20}} = \frac{4}{8} = \frac{1}{2}} \right).\)
Để \(\Delta D{\rm{EF}} \backsim \Delta {\rm{ILK(c - g - c)}}\) thì \(\hat E = \hat L\) (hai góc tạo bởi các cặp cạnh)
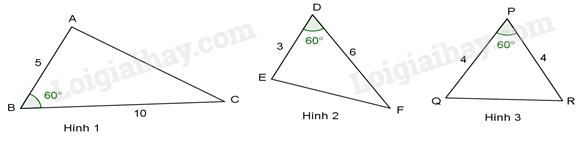
-
A.
Hình 1 và hình 2.
-
B.
Hình 2 và hình 3.
-
C.
Hình 1 và hình 3.
-
D.
Hình 1, hình 2 và hình 3.
Đáp án : A
Ta có: \(\frac{{BA}}{{BC}} = \frac{5}{{10}} = \frac{1}{2},\frac{{DE}}{{DF}} = \frac{3}{6} = \frac{1}{2},\frac{{PQ}}{{PR}} = \frac{4}{4} = 1\) ,
Xét \(\Delta ABC\) và \(\Delta EDF\) ta có: \(\frac{{BA}}{{BC}} = \frac{{DE}}{{DF}} = \frac{1}{2} \Leftrightarrow \frac{{BA}}{{DE}} = \frac{{BC}}{{DF}}\) và \(\hat B = \hat D = {60^0}(gt)\)
\( \Rightarrow \Delta ABC \backsim \Delta EDF(c - g - c)\)
Hình 1 và hình 2 là hai tam giác đồng dạng
-
A.
\({50^0}\)
-
B.
\({60^0}\)
-
C.
\({30^0}\)
-
D.
\({70^0}\)
Đáp án : B
Ta có: \(\frac{{BA}}{{BC}} = \frac{5}{{10}} = \frac{1}{2},\frac{{DE}}{{DF}} = \frac{3}{6} = \frac{1}{2}\)
\( \Rightarrow \frac{{BA}}{{BC}} = \frac{{DE}}{{DF}} = \frac{1}{2} \Leftrightarrow \frac{{BA}}{{DE}} = \frac{{BC}}{{DF}}\)
Để hai tam giác đã cho đồng dạng thì \(\hat B = \hat D = {60^0}\) .
Cho \(\Delta {A'}{B'}{C'}\) và \(\Delta ABC\) có \(\hat A = {\hat A'}\) . Để \(\Delta {A'}{B}{C'} \backsim \Delta ABC\) cần thêm điều kiện là:
-
A.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{A'}{C'}}}{{AC}}.\)
-
B.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{B'}{C'}}}{{BC}}.\)
-
C.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{BC}}{{{B'}{C'}}}.\)
-
D.
\(\frac{{{B'}{C'}}}{{BC}} = \frac{{AC}}{{{A'}{C'}}}.\)
Đáp án : A
Ta có: \(\widehat A = \widehat {{A'}}\) và \(\frac{{{A'}{B'}}}{{AB}} = \frac{{{A'}{C'}}}{{AC}}\) thì \(\Delta {A'}{B'}{C'} \backsim \Delta ABC\) (c-g-c)
Cho \(\Delta MNP \backsim \Delta KIH\) , biết \(\hat M = \hat K,MN = 2cm,MP = 8cm,KH = 4cm\) , thì KI bằng bao nhiêu:
-
A.
\(KI = 2cm.\)
-
B.
\(KI = 6cm.\)
-
C.
\(KI = 4cm.\)
-
D.
\(KI = 1cm.\)
Đáp án : D
\(\Delta MNP \backsim \Delta KIH \Rightarrow \frac{{MN}}{{KI}} = \frac{{MP}}{{KH}} \Leftrightarrow \frac{2}{{KI}} = \frac{8}{4} \Rightarrow KI = 1(cm)\)
Cho \(\Delta ABC\) , lấy hai điểm D và E lần lượt nằm bên cạnh AB và AC sao cho \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\) Kết luận nào sau đây sai:
-
A.
\(\Delta ADE \backsim \Delta ABC.\)
-
B.
\(DE//BC.\)
-
C.
\(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}.\)
-
D.
\(\widehat {ADE} = \widehat {ABC.}\)
Đáp án : C
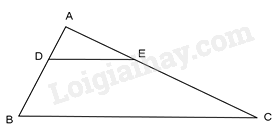
Xét \(\Delta ADE\) và \(\Delta ABC\) ta có: \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\) (gt); \(\hat A\) chung
\( \Rightarrow \Delta ADE \backsim \Delta ABC(c - g - c)\)
\( \Rightarrow \widehat {ADE} = \widehat {ABC}\) (cặp góc tương ứng)
\( \Rightarrow \frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\)
\( \Rightarrow DE//BC\) (định lý Ta lét đảo)
Cho \(\Delta ABC\) , có AC = 18cm; AB = 9cm; BC = 15cm . Trên cạnh AC lấy điểm N sao cho AN = 3cm , trên cạnh AB lấy điểm M sao cho AM = 6cm . Tính độ dài đoạn thẳng MN:
-
A.
MN= 6cm
-
B.
MN = 5cm
-
C.
MN = 8cm
-
D.
MN = 9cm
Đáp án : B

Ta có: \(\frac{{AN}}{{AB}} = \frac{3}{9} = \frac{1}{3},\frac{{AM}}{{AC}} = \frac{6}{{18}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} = \frac{1}{3}\)
Xét \(\Delta ANM\) và \(\Delta ABC\) có: \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}(cmt);\hat A\) chung
\(\begin{array}{l} \Rightarrow \Delta ANM \backsim \Delta ABC(c - g - c)\\ \Rightarrow \frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} = \frac{{MN}}{{CB}} = \frac{1}{3} \Rightarrow \frac{{MN}}{{15}} = \frac{1}{3} \Rightarrow MN = \frac{{15}}{3} = 5(cm).\end{array}\)
-
A.
x = 15
-
B.
x = 16
-
C.
x = 7
-
D.
x = 8
Đáp án : A
Ta có \(\frac{{AB}}{{AC}} = \frac{6}{9} = \frac{2}{3},\frac{{AC}}{{CD}} = \frac{9}{{13,5}} = \frac{2}{3}\)
\( \Rightarrow \frac{{AB}}{{AC}} = \frac{{AC}}{{CD}} = \frac{2}{3}\)
Xét \(\Delta ABC\) và \(\Delta CAD\) có: \(\frac{{AB}}{{AC}} = \frac{{AC}}{{CD}}(cmt),\widehat {BAC} = \widehat {ACD}\) (so le trong, AB//CD )
\(\begin{array}{l} \Rightarrow \Delta ABC \backsim \Delta CAD(c - g - c)\\ \Rightarrow \frac{{AB}}{{AC}} = \frac{{CA}}{{CD}} = \frac{{BC}}{{AD}} = \frac{2}{3}\\ \Rightarrow \frac{{10}}{x} = \frac{2}{3} \Rightarrow x = \frac{{10.3}}{2} = 15\end{array}\)
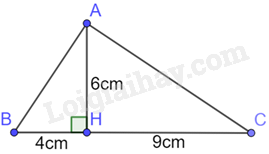
Cho \(\Delta ABC\) vuông tại A, đường cao \(AH(H \in BC)\) . Biết AB = 3cm, AC = 6cm,
AH = 2cm, HC = 4cm. Hệ thức nào sau đây đúng:
-
A.
\(A{C^2} = CH.BH\)
-
B.
\(AB.AH = HC.AC\)
-
C.
\(AB.HC = AH.AC\)
-
D.
\(AB.AC = AH.HC\)
Đáp án : C
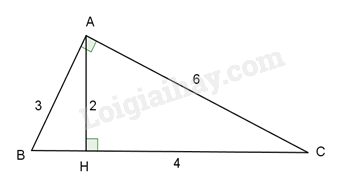
Xét \(\Delta ABC\) và \(\Delta HAC\) có: \(\frac{{AB}}{{AC}} = \frac{3}{6} = \frac{1}{2},\frac{{AH}}{{HC}} = \frac{2}{4} = \frac{1}{2}\)
\(\begin{array}{l} \Rightarrow \frac{{AB}}{{AC}} = \frac{{AH}}{{HC}} = \frac{1}{2}\\ \Rightarrow AB.HC = AH.AC\end{array}\)
Cho hình thang vuông \(ABCD(\hat A = \hat D = {90^0})\) có AB = 16cm, CD = 25cm,
BD = 20cm . Độ dài cạnh BC là:
-
A.
10 cm
-
B.
12cm
-
C.
15cm
-
D.
9cm
Đáp án : C
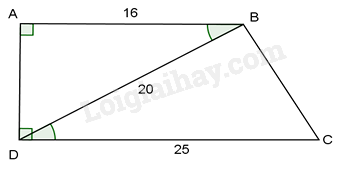
\(\Delta ABD\) và \(\Delta BDC\) có: \(\widehat {ABD} = \widehat {BDC}\) (so le trong, AB//CD)
\(\frac{{AB}}{{BD}} = \frac{{BD}}{{DC}}\) (Vì \(\frac{{16}}{{20}} = \frac{{20}}{{25}})\)
Do đó \(\Delta ABD \backsim \Delta BDC(c - g - c)\)
Ta có \({\rm{\hat A = 90}}{}^0\) nên \(\widehat {DBC} = {90^0}\) . Theo định lí Pytago, ta có:
\(B{C^2} = C{D^2} - B{D^2} = {25^2} - {20^2} = {15^2}\) .Vậy BC= 15 (cm)
Cho \(\Delta MNP \backsim \Delta EFH\) theo tỉ số k. Gọi \(M{M'},E{E'}\) lần lượt là hai trung tuyến của \(\Delta MNP\) và \(\Delta EFH\) . Khi đó ta chứng minh được:
-
A.
\(\frac{{E{E'}}}{{M{M'}}} = k\)
-
B.
\(\frac{{M{M '}}}{{E{E '}}} = k\)
-
C.
\(\frac{{M{M '}}}{{E{E '}}} = {k^2}\)
-
D.
\(\frac{{E{E '}}}{{M{M '}}} = {k^2}\)
Đáp án : B
Ta có tỉ số đồng dạng bằng với tỉ số đường trung tuyến tương ứng \(\frac{{M{M'}}}{{E{E '}}} = k\)
Tỉ số đồng dạng bằng với tỉ số đường trung tuyến tương ứng.
Cho tam giác nhọn ABC có \(\hat C = {60^0}\) . Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của tam giác ABC, ACD. Tính số đo góc AKH.
-
A.
\({30^0}\)
-
B.
\({60^0}\)
-
C.
\({45^0}\)
-
D.
\({50^0}\)
Đáp án : B
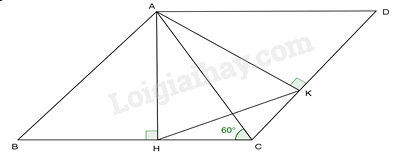
Vì \(AD.AH = AB.AK( = {S_{ABCD}})\) nên \(\frac{{AH}}{{AK}} = \frac{{AB}}{{AD}} = \frac{{AB}}{{BC}}\)
Ta lại có AB//CD (vì ABCD là hình bình hành) mà \(AK \bot DC \Leftrightarrow AK \bot AB \Rightarrow \widehat {BAK} = {90^0}\)
Từ đó \(\widehat {HAK} = \widehat {ABC}\) (cùng phụ với \(\widehat {BAH}\) )
Nên \(\Delta AKH \backsim \Delta BCA(c - g - c) \Rightarrow \widehat {AKH} = \widehat {ACB} = {60^0}\)
Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm . Hỏi góc B bằng bao nhiêu lần góc A?
-
A.
\(\hat B = \frac{{\hat A}}{3}\)
-
B.
\(\hat B = \frac{2}{3}\hat A\)
-
C.
\(\hat B = \frac{{\hat A}}{2}\)
-
D.
\(\hat B = \hat A\)
Đáp án : C
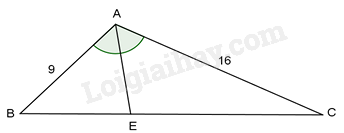
Kẻ đường phân giác AE của \(\Delta ABC\) . Theo tính chất đường phân giác, ta có:
\(\frac{{BE}}{{EC}} = \frac{{AB}}{{AC}} = \frac{9}{{16}}\) hay \(\frac{{BE}}{{AB}} = \frac{{CE}}{{AC}}\)
Nên \(\frac{{BE + EC}}{{AB+AC}} = \frac{{20}}{{9+16}}=\frac{4}{5}\)
Hay \(\frac{{CE}}{{AC}} = \frac{{CE}}{{16}} =\frac{4}{5} \Rightarrow EC = 12,8(cm)\)
Xét \(\Delta ACB\) và \(\Delta ECA\) có: \(\hat C\) là góc chung
\(\frac{{AC}}{{EC}} = \frac{{CB}}{{CA}}\) (vì \(\frac{{16}}{{12,8}} = \frac{{20}}{{16}})\)
Do đó \(\Delta ACB \backsim \Delta ECA\) (c-g-c) suy ra \(\hat B = \widehat {CAE}\) tức là \(\hat B = \frac{{\hat A}}{2}\)
Cho hình thoi ABCD cạnh a, có \(\hat A = {60^0}\) . Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính \(\widehat {BKD}\) .
-
A.
\(\widehat {BKD} = {60^0}\)
-
B.
\(\widehat {BKD} = {100^0}\)
-
C.
\(\widehat {BKD} = {120^0}\)
-
D.
\(\widehat {BKD} = {115^0}\)
Đáp án : C
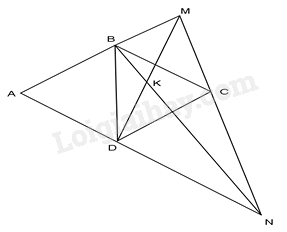
Do BC//AN (Vì \(N \in AD\) ) nên ta có: \(\frac{{MB}}{{AB}} = \frac{{MC}}{{NC}}\) (1)
Do CD//AM (Vì \(M \in AB\) ) nên ta có: \(\frac{{MC}}{{NC}} = \frac{{AD}}{{DN}}\) (2)
Từ (1) và (2) \( \Rightarrow \frac{{MB}}{{AB}} = \frac{{AD}}{{DN}}\)
\(\Delta ABD\) có AB = AD (định nghĩa hình thoi) và \(\hat A = {60^0}\) nên \(\Delta ABD\) là tam giác đều
\( \Rightarrow AB = BD = DA\)
Từ \( \Rightarrow \frac{{MB}}{{AB}} = \frac{{AD}}{{DN}}(cmt) \Rightarrow \frac{{MB}}{{BD}} = \frac{{BD}}{{DN}}\)
Mặt khác \(\widehat {MBD} = \widehat {DBN} = {120^0}\)
Xét \(\Delta MBD\) và \(\Delta BDN\) có: \(\frac{{MB}}{{BD}} = \frac{{BD}}{{DN}},\widehat {MBD} = \widehat {DBN}\)
\(\begin{array}{l} \Rightarrow \Delta MBD \backsim \Delta BDN(c - g - c)\\ \Rightarrow \widehat {BMD} = \widehat {DBN}\end{array}\)
Xét \(\Delta MBD\) và \(\Delta KBD\) có: \(\widehat {MBD} = \widehat {DBN},\widehat {BDM}\) chung
\( \Rightarrow \widehat {BKD} = \widehat {MDB} = {120^0}\)
Vậy \(\widehat {BKD} = {120^0}\)
Cho hình thang vuông ABCD \(\left( {\hat A = \hat D = {{90}^0}} \right)\) có AB = 4cm, CD = 9cm, BC = 13cm . Gọi M là trung điểm của AD. Tính \(\widehat {BMC}\) .
-
A.
\({60^0}\)
-
B.
\({110^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Đáp án : D
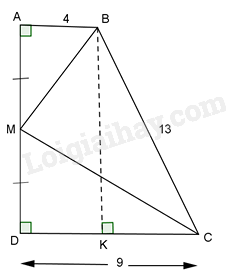
Kẻ \(BK \bot CD(K \in CD)\) thì tứ giác ABKD là hình có 3 góc vuông nên nó là hình chữ nhật.
Do đó: \(DK = AB = 4(cm) \Rightarrow KC = DC - DK = 9 - 4 = 5(cm)\)
Tam giác KBC vuông tại K, theo định lý Pytago ta có:
\(B{C^2} = C{K^2} + K{B^2}\) hay \({13^2} = {5^2} + K{B^2} \Rightarrow KB = 12(cm)\) nên \( \Rightarrow AD = KB = 12(cm)\)
M là trung điểm của AD nên \(AM = MD = \frac{1}{2}AD = 6(cm)\)
Xét \(\Delta AMB\) và \(\Delta DCM\) có: \(\frac{{AB}}{{DM}} = \frac{4}{6} = \frac{6}{9} = \frac{{AM}}{{DC}},\widehat {MAB} = \widehat {MDC} = {90^0}\)
\( \Rightarrow \Delta AMB \backsim \Delta DCM(c - g - c)\)
\( \Rightarrow \widehat {AMB} = \widehat {DCM}\) mà \(\widehat {DMC} + \widehat {DCM} = {90^0}\)
\( \Rightarrow \widehat {AMB} + \widehat {DCM} = {90^0} \Rightarrow \widehat {BMC} = {90^0}\)