Trắc nghiệm Bài 8: Trường hợp đồng dạng thứ ba của tam giác Toán 8 Cánh diều
Đề bài
Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
-
A.
\(2AC = CH.BC\)
-
B.
\(A{C^2} = \frac{1}{2}CH.BC\)
-
C.
\(A{C^2} = CH.BC\)
-
D.
\(A{C^2} = 2CH.BC\)
Cho tam giác \(ABC\) cân tại \(A\) , đường cao \(CE\) . Tính \(AB\) , biết \(BC = 24\) cm và \(BE = 9\) cm.
-
A.
16cm
-
B.
32cm
-
C.
24cm
-
D.
18cm
-
A.
\(AI.AN + BI.BM = 2A{B^2}\)
-
B.
\(AI.AN + BI.BM = A{B^2}\)
-
C.
\(AI.AN + 2BI.BM = A{B^2}\)
-
D.
\(2AI.AN + BI.BM = A{B^2}\)
-
A.
\(y = 10\)
-
B.
\(x = 4,8\)
-
C.
A, B đều đúng
-
D.
A, B đều sai
Cho tam giác ABC cân tại A, \(AC = 20cm,BC = 24cm.\) Các đường cao AD và CE cắt nhau tại H. Khi đó,
-
A.
\(HD = 12cm\)
-
B.
\(HD = 6cm\)
-
C.
\(HD = 9cm\)
-
D.
\(HD = 10cm\)
Cho tam giác ABC vuông tại A, đường cao AH chia đoạn BC thành hai đoạn thẳng \(HB = 7cm,HC = 18cm.\) Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác thành 2 phần có diện tích bằng nhau. Khi đó,
-
A.
\(CE = 15cm\)
-
B.
\(CE = 16cm\)
-
C.
\(CE = 12cm\)
-
D.
\(CE = 10cm\)
Cho hình bình hành ABCD \(\left( {AC > AB} \right)\) . Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD và H là hình chiếu của B trên AC.
Chọn đáp án đúng.
-
A.
\(AB.AE + AD.AK = 2A{C^2}\)
-
B.
\(2AB.AE + AD.AK = A{C^2}\)
-
C.
\(AB.AE + 2AD.AK = A{C^2}\)
-
D.
\(AB.AE + AD.AK = A{C^2}\)
Cho tam giác ABC vuông tại A. Lấy một điểm M bất kì trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E. Khi đó:
-
A.
\(BM.BD + CM.CA = \frac{1}{2}B{C^2}\)
-
B.
\(BM.BD + 2CM.CA = B{C^2}\)
-
C.
\(BM.BD + CM.CA = B{C^2}\)
-
D.
\(BM.BD + CM.CA = 2B{C^2}\)
Cho tam giác ABC cân tại A, đường cao CE. Biết rằng \(BE = 3cm,BC = 8cm.\)
Độ dài đoạn thẳng AB là:
-
A.
\(\frac{{34}}{3}cm\)
-
B.
32cm
-
C.
\(\frac{{32}}{3}cm\)
-
D.
35cm
Cho tam giác ABC vuông tại A có \(\widehat B = {30^0}\), tam giác MNP vuông tại M có \(\widehat N = {60^{0.}}\)
Chọn đáp án đúng.
-
A.
\(AB.PN = MP.BC\)
-
B.
\(AB.MP = PN.BC\)
-
C.
\(AB.MP = 2PN.BC\)
-
D.
\(AB.PN = 2MP.BC\)
-
A.
\(D{H^2} = HE + 2HF\)
-
B.
\(D{H^2} = HE.HF\)
-
C.
\(D{H^2} = HE + HF\)
-
D.
\(D{H^2} = HE - HF\)
Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho \(AM = 2m,AM \bot AB\) và đo được góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A’M’B’ vuông tại A’ có \(A'M' = 1cm,\;\widehat {A'M'B'} = \widehat {AMB}\) và đo được \(A'B' = 5cm\) (hình vẽ dưới). Khoảng cách từ A đến B bằng:

-
A.
4m
-
B.
6m
-
C.
8m
-
D.
10m
-
A.
\(\frac{{BC}}{{BE}} = 2\frac{{BD}}{{BA}}\)
-
B.
\(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)
-
C.
\(2\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)
-
D.
A, B, C đều sai
Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
-
A.
\(\Delta ACH \backsim \Delta BCA\)
-
B.
\(\Delta ACH \backsim \Delta CBA\)
-
C.
\(\Delta ACH \backsim \Delta BAC\)
-
D.
\(\Delta ACH \backsim \Delta CBA\)
Cho các mệnh đề sau. Chọn câu đúng .
(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
(II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
-
A.
(I) đúng, (II) sai
-
B.
(I) sai, (II) đúng
-
C.
(I) và (II) đều sai
-
D.
(I) và (II) đều đúng
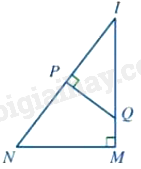
-
A.
\(\Delta IPQ \backsim \Delta IMN\)
-
B.
\(\Delta IPQ = \Delta IMN\)
-
C.
\(\Delta IPQ \backsim \Delta INM\)
-
D.
\(\Delta IPQ \backsim \Delta MNI\)
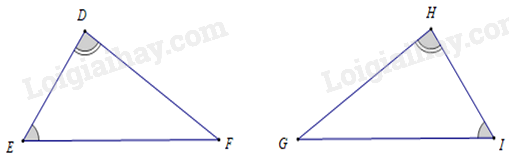
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\widehat B = \widehat F\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
Nếu \(\Delta MNP\) và \(\Delta DEF\) có \(\widehat{M}=\widehat{D}=90{}^\circ \) , \(\widehat{P}=50{}^\circ \) . Để \(\Delta MNP\,\backsim \,\Delta DEF\) thì cần thêm điều kiện
-
A.
\(\widehat{E}=50{}^\circ \) .
-
B.
\(\widehat{F}=60{}^\circ \) .
-
C.
\(\widehat{F}=40{}^\circ \) .
-
D.
\(\widehat{E}=40{}^\circ \)
Nếu \(\Delta DEF\) và \(\Delta SRK\) có \(\widehat{D}=70{}^\circ \) ; \(\widehat{E}=60{}^\circ \) ; \(\widehat{S}=70{}^\circ \) ; \(\widehat{K}=50{}^\circ \) thì
-
A.
\(\frac{DE}{SR}=\frac{DF}{SK}=\frac{EF}{RK}\) .
-
B.
\(\frac{DE}{SR}=\frac{DF}{RK}=\frac{EF}{SK}\) .
-
C.
\(\frac{DE}{SR}=\frac{DF}{SR}=\frac{EF}{RK}\) .
-
D.
\(\frac{DE}{RK}=\frac{DF}{SK}=\frac{EF}{SR}\)
-
A.
\(\Delta ABC\,\backsim \Delta ABH\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta HAB\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta AHB\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta HBA\) .
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\). Hệ thức nào sau đây đúng?
-
A.
\(AB = BC.BH\).
-
B.
\(A{C^2} = CH.BH\).
-
C.
\(A{H^2} = BH.CH\).
-
D.
\(AH = CH.BH\).
Cho hình thang \(ABCD\) \(\left( {AB\,{\rm{//}}\,CD} \right)\), \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\). Khẳng định nào sau đây đúng
-
A.
\({\rm{\Delta }}OAB \backsim \,\Delta ODC\).
-
B.
\({\rm{\Delta }}CAB \backsim {\rm{\Delta }}CDA\).
-
C.
\({\rm{\Delta }}OAB \backsim {\rm{\Delta }}OCD\).
-
D.
\({\rm{\Delta }}OAD \backsim {\rm{\Delta }}OBC\).
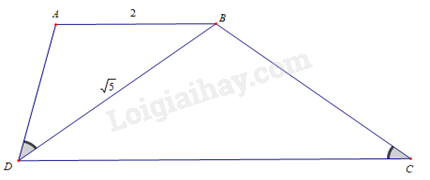
Cho hình thang \(ABCD\,\,\left( {AB\,{\rm{//}}\,CD} \right)\), \(\widehat {ADB} = \widehat {BCD}\), \(AB = 2\,{\rm{cm}}\), \(BD = \sqrt 5 \,{\rm{cm}}\). Độ dài đoạn thẳng \(CD\) là
-
A.
\(2\sqrt 5 \,{\rm{cm}}\).
-
B.
\(\sqrt 5 - 2\,{\rm{cm}}\).
-
C.
\(\frac{{\sqrt 5 }}{2}\,{\rm{cm}}\).
-
D.
\(2,5\,{\rm{cm}}\).
Cho hình thang vuông \(ABCD\), \(\left( {\widehat A = \widehat D = 90^\circ } \right)\) có \(DB \bot BC\), \(AB = 4\,{\rm{cm}}\), \(CD = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(BD\) là
-
A.
\(8\,{\rm{cm}}\).
-
B.
\(12\,{\rm{cm}}\).
-
C.
\(9\,{\rm{cm}}\).
-
D.
\(6\,{\rm{cm}}\).
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\) biết \(BH = 4\,{\rm{cm}}\), \(CH = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(AH\) là
-
A.
\(4,8\,{\rm{cm}}\).
-
B.
\(5\,{\rm{cm}}\).
-
C.
\(6\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
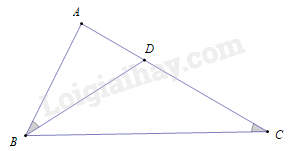
Cho hình vẽ, biết \(\widehat {ACB} = \widehat {ABD}\), \(AB = 3\,{\rm{cm}}\), \(AC = 4,5\,{\rm{cm}}\). Độ dài đoạn thẳng \(AD\) là
-
A.
\(2\,{\rm{cm}}\).
-
B.
\(2,5\,{\rm{cm}}\).
-
C.
\(3\,{\rm{cm}}\).
-
D.
\(1,5\,{\rm{cm}}\).
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 30\,{\rm{cm}}\), \(AC = 40\,{\rm{cm}}\). Kẻ đường cao \(AH\)\(\left( {H \in BC} \right)\). Độ dài đường cao \(AH\) là
-
A.
\(18\,{\rm{cm}}\).
-
B.
\(24\,{\rm{cm}}\).
-
C.
\(32\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
\(\Delta ABC\) cân tại \(A\), hai đường cao \(AH\) và \(BK\), cho \(BC = 6\,{\rm{cm}}\), \(AB = 5\,{\rm{cm}}\). Độ dài đoạn thẳng \(BK\) là
-
A.
\(4,5\,{\rm{cm}}\).
-
B.
\(4,8\,{\rm{cm}}\).
-
C.
\(3\,{\rm{cm}}\).
-
D.
\(4\,{\rm{cm}}\).
\(\Delta ABC\) vuông tại \(A\) có \(\widehat B = 60^\circ \), \(BD\) là phân giác \(\widehat B\), \(AC = 18\,{\rm{cm}}\). Độ dài đoạn thẳng \(BD\) là
-
A.
\(12\,{\rm{cm}}\).
-
B.
\(10\,{\rm{cm}}\).
-
C.
\(9\,{\rm{cm}}\).
-
D.
\(8\,{\rm{cm}}\).
-
A.
x = 15
-
B.
x = 16
-
C.
x = 7
-
D.
x = 8
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}=\widehat{D}\) , \(\widehat{C}=\widehat{F}\) thì
-
A.
\(\Delta ABC\backsim \Delta DEF\) .
-
B.
\(\Delta CAB\backsim \Delta DEF\) .
-
C.
\(\Delta ABC\backsim \Delta DFE\) .
-
D.
\(\Delta CAB \backsim \Delta DFE\)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}={{70}^{\circ }}\) , \(\widehat{C}={{60}^{\circ }}\) , \(\widehat{E}={{50}^{\circ }}\) , \(\widehat{F}={{70}^{\circ }}\) thì
-
A.
\(\Delta ACB\,\,\backsim \,\,\Delta FED\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta FED\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta DEF\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta DFE\) .
Cho \(\Delta ABC\,\backsim \,\Delta {A}'{B}'{C}'\) (g – g ). Khẳng định nào sau đây đúng
-
A.
\(\widehat{A}=\widehat{{{B}'}}\) .
-
B.
\(AB={A}'{B}'\) .
-
C.
\(\frac{AB}{AC}=\frac{{A}'{B}'}{{A}'{C}'}\) .
-
D.
\(\frac{AB}{AC}=\frac{{A}'{C}'}{{A}'{B}'}\) .
-
A.
\(\Delta HIG\backsim \Delta DEF\) .
-
B.
\(\Delta IGH\backsim \Delta DEF\) .
-
C.
\(\Delta HIG\backsim \Delta DFE\) .
-
D.
\(\Delta HGI\backsim \Delta DEF\) .
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu
-
A.
ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
có hai cặp cạnh tương ứng bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Nếu \(\Delta ABC\) và \(\Delta MNP\) có \(\widehat{A}=\widehat{N}\) ; \(\widehat{B}=\widehat{M}\) thì
-
A.
\(\Delta ABC\backsim \,\Delta MNP\) .
-
B.
\(\Delta CAB\backsim \Delta NMP\) .
-
C.
\(\Delta ABC\backsim \Delta PMN\) .
-
D.
\(\Delta ABC\backsim \Delta NMP\) .
Lời giải và đáp án
Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
-
A.
\(2AC = CH.BC\)
-
B.
\(A{C^2} = \frac{1}{2}CH.BC\)
-
C.
\(A{C^2} = CH.BC\)
-
D.
\(A{C^2} = 2CH.BC\)
Đáp án : C
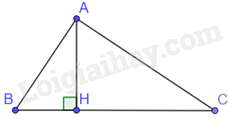
Tam giác ACH và tam giác CBA có: \(\widehat {AHC} = \widehat {BAC} = {90^0},\widehat C\;chung\)
Do đó, \(\Delta ACH \backsim \Delta BCA(g.g) \Rightarrow \frac{{AC}}{{BC}} = \frac{{CH}}{{AC}} \Rightarrow A{C^2} = CH.BC\)
Cho tam giác \(ABC\) cân tại \(A\) , đường cao \(CE\) . Tính \(AB\) , biết \(BC = 24\) cm và \(BE = 9\) cm.
-
A.
16cm
-
B.
32cm
-
C.
24cm
-
D.
18cm
Đáp án : B
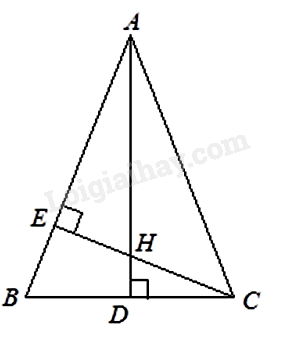
Kẻ đường cao \(AD\) . Xét \(\Delta CBE\) và \(\Delta ABD\) có \(\widehat {BEC} = \widehat {ADB} = {90^\circ }\) và \(\hat B\) chung nên \(\Delta CBE \backsim \Delta ABD \Rightarrow \frac{{BC}}{{AB}} = \frac{{BE}}{{BD}}\) hay \(\frac{{24}}{{AB}} = \frac{9}{{12}}\)
\( \Rightarrow AB = 32{\rm{cm}}\) .
-
A.
\(AI.AN + BI.BM = 2A{B^2}\)
-
B.
\(AI.AN + BI.BM = A{B^2}\)
-
C.
\(AI.AN + 2BI.BM = A{B^2}\)
-
D.
\(2AI.AN + BI.BM = A{B^2}\)
Đáp án : B
Tam giác ABN và tam giác AIP có: \(\widehat N = \widehat {IPA} = {90^0},\widehat {BAN}\;chung\)
Do đó, \(\Delta ABN \backsim \Delta AIP \Rightarrow \frac{{AB}}{{AI}} = \frac{{AN}}{{AP}} \Rightarrow AI.AN = AP.AB\)
Tam giác AMB và tam giác IPB có: \(\widehat M = \widehat {IPB} = {90^0},\widehat {ABM}\;chung\)
Do đó, \(\Delta AMB \backsim \Delta IPB \Rightarrow \frac{{AB}}{{BI}} = \frac{{BM}}{{BP}} \Rightarrow AB.BP = BI.BM\)
Vậy \(AI.AN + BI.BM = AP.AB + AB.PB = AB\left( {AP + PB} \right) = A{B^2}\)
-
A.
\(y = 10\)
-
B.
\(x = 4,8\)
-
C.
A, B đều đúng
-
D.
A, B đều sai
Đáp án : B
Tam giác ADO và tam giác ECO có: \(\widehat {DAO} = \widehat {CEO} = {90^0},\widehat {AOD} = \widehat {COE}\) (hai góc đối đỉnh)
Do đó, \(\Delta ADO \backsim \Delta ECO \Rightarrow \frac{{AD}}{{EC}} = \frac{{DO}}{{CO}} \Rightarrow \frac{4}{x} = \frac{5}{6} \Rightarrow x = 4,8\)
Áp dụng định lý Pytago vào tam giác ADO vuông tại A ta có:
\(A{D^2} + A{O^2} = O{D^2}\) \( \Rightarrow A{O^2} = D{O^2} - A{D^2} = 9 \Rightarrow AO = 3\)
Tam giác CEO và tam giác CAB có: \(\widehat {CEO} = \widehat {CAB} = {90^0},\widehat {C}\;chung\)
Do đó, \(\Delta CEO \backsim \Delta CAB \Rightarrow \frac{{CO}}{{CB}} = \frac{{CE}}{{CA}} \Rightarrow \frac{{CO}}{{EC + EB}} = \frac{{CE}}{{CO + AO}} \Rightarrow \frac{6}{{4,8 + y}} = \frac{{4,8}}{{6 + 3}} \Rightarrow y = 6,45\)
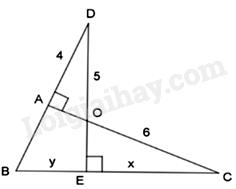
Cho tam giác ABC cân tại A, \(AC = 20cm,BC = 24cm.\) Các đường cao AD và CE cắt nhau tại H. Khi đó,
-
A.
\(HD = 12cm\)
-
B.
\(HD = 6cm\)
-
C.
\(HD = 9cm\)
-
D.
\(HD = 10cm\)
Đáp án : C
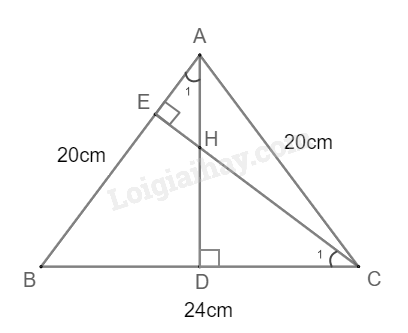
Tam giác ABC cân tại A nên \(BD = DC = \frac{{BC}}{2} = 12\left( {cm} \right)\)
Áp dụng định lý Pytago vào tam giác ADC vuông tại D ta có: \(A{D^2} = A{C^2} - D{C^2} = {16^2} \Rightarrow AD = 16cm\)
Tam giác CDH và tam giác ADB có: \(\widehat {CDH} = \widehat {ADB} = {90^0},\widehat {{C_1}} = \widehat {{A_1}}\) (cùng phụ với góc B)
Do đó, \(\Delta CDH \backsim \Delta ADB \Rightarrow \frac{{HD}}{{BD}} = \frac{{CD}}{{AD}} \Rightarrow \frac{{HD}}{{12}} = \frac{{12}}{{16}} = \frac{3}{4}\)
Suy ra: \(HD = 9cm\)
Cho tam giác ABC vuông tại A, đường cao AH chia đoạn BC thành hai đoạn thẳng \(HB = 7cm,HC = 18cm.\) Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác thành 2 phần có diện tích bằng nhau. Khi đó,
-
A.
\(CE = 15cm\)
-
B.
\(CE = 16cm\)
-
C.
\(CE = 12cm\)
-
D.
\(CE = 10cm\)
Đáp án : A
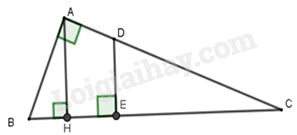
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Tam giác AHC và tam giác ABC có: \(\widehat {AHC} = \widehat {BAC} = {90^0},\widehat C\;chung.\) Do đó, \(\Delta ACH \backsim \Delta BCA\)
Ta có: \({S_{DEC}} = \frac{1}{2}{S_{ABC}}\left( 1 \right)\) , \(\frac{{{S_{AHC}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}HC.AH}}{{\frac{1}{2}BC.AH}} = \frac{{HC}}{{BC}} = \frac{{18}}{{25}} \Rightarrow {S_{AHC}} = \frac{{18}}{{25}}{S_{ABC}}\left( 2 \right)\)
Từ (1) và (2) ta có: \({S_{DEC}}:{S_{AHC}} = \frac{1}{2}:\frac{{18}}{{25}} = \frac{{25}}{{36}} = {\left( {\frac{5}{6}} \right)^2}\left( 3 \right)\)
Tam giác DEC và tam giác AHC có: \(\widehat {DEC} = \widehat {AHC} = {90^0},\widehat C\;chung\)
\(\Delta DEC \backsim \Delta AHC \Rightarrow \frac{{{S_{DEC}}}}{{{S_{AHC}}}} = {\left( {\frac{{EC}}{{HC}}} \right)^2}\left( 4 \right)\)
Từ (3) và (4) ta có: \(\frac{{EC}}{{HC}} = \frac{5}{6}\) \( \Rightarrow \) \(\frac{{EC}}{{18}} = \frac{5}{6} \Rightarrow EC = 15cm\)
Cho hình bình hành ABCD \(\left( {AC > AB} \right)\) . Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD và H là hình chiếu của B trên AC.
Chọn đáp án đúng.
-
A.
\(AB.AE + AD.AK = 2A{C^2}\)
-
B.
\(2AB.AE + AD.AK = A{C^2}\)
-
C.
\(AB.AE + 2AD.AK = A{C^2}\)
-
D.
\(AB.AE + AD.AK = A{C^2}\)
Đáp án : D
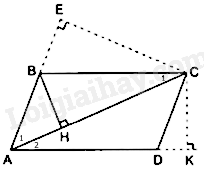
Tam giác AHB và tam giác AEC có: \(\widehat {{A_1}}chung,\widehat {AHB} = \widehat E = {90^0}\)
Do đó, \(\Delta AHB \backsim \Delta AEC \Rightarrow \frac{{AH}}{{AE}} = \frac{{AB}}{{AC}} \Rightarrow AB.AE = AC.AH\)
Vì BC// AD (do ABCD là hình bình hành) nên \(\widehat {{C_1}} = \widehat {{A_2}}\) , mà \(\widehat {BHC} = \widehat K = {90^0}\)
Do đó, \(\Delta AKC \backsim \Delta CHB \Rightarrow \frac{{AK}}{{CH}} = \frac{{AC}}{{CB}} \Rightarrow AK.CB = AC.CH\)
Vì ABCD là hình bình hành nên \(BC = AD\)
Do đó, \(AD.AK = AC.CH\left( 3 \right)\)
Từ (1), (2) và (3) ta có:
\(AB.AE + AD.AK = AC\left( {AH + CH} \right) = A{C^2}\)
Cho tam giác ABC vuông tại A. Lấy một điểm M bất kì trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E. Khi đó:
-
A.
\(BM.BD + CM.CA = \frac{1}{2}B{C^2}\)
-
B.
\(BM.BD + 2CM.CA = B{C^2}\)
-
C.
\(BM.BD + CM.CA = B{C^2}\)
-
D.
\(BM.BD + CM.CA = 2B{C^2}\)
Đáp án : C
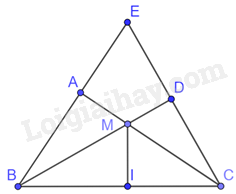
Kẻ MI vuông góc với BC tại I
Tam giác BIM và tam giác BDC có: \(\widehat {BIM} = \widehat {BDC} = {90^0},\widehat {MBC}\;chung\)
Do đó, \(\Delta BIM \backsim \Delta BDC \Rightarrow \frac{{BM}}{{BC}} = \frac{{BI}}{{BD}} \Rightarrow BM.BD = BC.BI\left( 1 \right)\)
Chứng minh tương tự ta có: \(\Delta ICM \backsim \Delta ACB \Rightarrow \frac{{CM}}{{BC}} = \frac{{CI}}{{CA}} \Rightarrow CM.CA = BC.CI\left( 2 \right)\)
Từ (1) và (2) ta có: \(BM.BD + CM.CA = BC.BI + BC.CI = BC\left( {BI + CI} \right) = B{C^2}\)
Cho tam giác ABC cân tại A, đường cao CE. Biết rằng \(BE = 3cm,BC = 8cm.\)
Độ dài đoạn thẳng AB là:
-
A.
\(\frac{{34}}{3}cm\)
-
B.
32cm
-
C.
\(\frac{{32}}{3}cm\)
-
D.
35cm
Đáp án : C
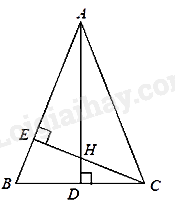
Kẻ đường cao AD của tam giác ABC.
Vì tam giác ABC cân tại A nên AD là đường cao đồng thời là đường trung tuyến
Suy ra: \(BD = \frac{1}{2}BC = 4cm\)
Xét tam giác CBE và tam giác ABD có: \(\widehat {BEC} = \widehat {ADB} = {90^0}\) và góc B chung
Do đó, \(\Delta CBE \backsim \Delta ABD\left( {g.g} \right) \Rightarrow \frac{{BC}}{{AB}} = \frac{{BE}}{{BD}} \Rightarrow AB = \frac{{BD.BC}}{{BE}} = \frac{{32}}{3}\left( {cm} \right)\)
Cho tam giác ABC vuông tại A có \(\widehat B = {30^0}\), tam giác MNP vuông tại M có \(\widehat N = {60^{0.}}\)
Chọn đáp án đúng.
-
A.
\(AB.PN = MP.BC\)
-
B.
\(AB.MP = PN.BC\)
-
C.
\(AB.MP = 2PN.BC\)
-
D.
\(AB.PN = 2MP.BC\)
Đáp án : A
Tam giác ABC vuông tại A nên \(\widehat B + \widehat C = {90^0} \Rightarrow \widehat C = {90^0} - \widehat B = {60^0}\)
Tam giác ABC và tam giác MNP có: \(\widehat A = \widehat M = {90^0},\widehat C = \widehat N\left( { = {{60}^0}} \right)\)
Do đó, \(\Delta ABC \backsim \Delta MPN(g.g) \Rightarrow \frac{{AB}}{{MP}} = \frac{{BC}}{{PN}} \Rightarrow AB.PN = MP.BC\)
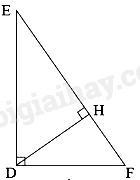
-
A.
\(D{H^2} = HE + 2HF\)
-
B.
\(D{H^2} = HE.HF\)
-
C.
\(D{H^2} = HE + HF\)
-
D.
\(D{H^2} = HE - HF\)
Đáp án : B
Ta có: \(\widehat {EDH} + \widehat {HDF} = \widehat F + \widehat {HDF}\left( { = {{90}^0}} \right) \Rightarrow \widehat {EDH} = \widehat F\)
Tam giác EDH và tam giác DFH có:
\(\widehat {EHD} = \widehat {FHD} = {90^0},\widehat {EDH} = \widehat F\)
Do đó, \(\Delta EDH \backsim \Delta DFH(g.g)\) nên \(\frac{{DH}}{{FH}} = \frac{{EH}}{{DH}} \Rightarrow D{H^2} = EH.FH\)
Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho \(AM = 2m,AM \bot AB\) và đo được góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A’M’B’ vuông tại A’ có \(A'M' = 1cm,\;\widehat {A'M'B'} = \widehat {AMB}\) và đo được \(A'B' = 5cm\) (hình vẽ dưới). Khoảng cách từ A đến B bằng:

-
A.
4m
-
B.
6m
-
C.
8m
-
D.
10m
Đáp án : D
Đổi \(1cm = 0,01m;\;5cm = 0,05m\)
Tam giác AMB và tam giác A’M’B’ có: \(\widehat {BAM} = \widehat {B'A'M'} = {90^0},\widehat {AMB} = \widehat {A'M'B'}\)
Do đó,\(\Delta AMB \backsim \Delta A'M'B'(g.g)\)
Suy ra, \(\frac{{AB}}{{A'B'}} = \frac{{AM}}{{A'M'}} = \frac{2}{{0,01}} = 200 \Rightarrow AB = 200.A'B' = 10\left( m \right)\)
-
A.
\(\frac{{BC}}{{BE}} = 2\frac{{BD}}{{BA}}\)
-
B.
\(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)
-
C.
\(2\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)
-
D.
A, B, C đều sai
Đáp án : B
Ta có: \(\widehat A + \widehat C = \widehat A + \widehat E\left( { = {{90}^0}} \right) \Rightarrow \widehat C = \widehat E\)
Xét tam giác ABE và tam giác DCB có: \(\widehat {ABE} = \widehat {DBC} = {90^0},\widehat E = \widehat C\)
Do đó, \(\Delta ABE \backsim \Delta DBC(g.g)\)
Do đó, \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)
Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
-
A.
\(\Delta ACH \backsim \Delta BCA\)
-
B.
\(\Delta ACH \backsim \Delta CBA\)
-
C.
\(\Delta ACH \backsim \Delta BAC\)
-
D.
\(\Delta ACH \backsim \Delta CBA\)
Đáp án : A
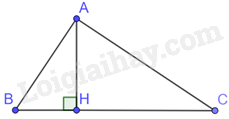
Tam giác ACH và tam giác CBA có: \(\widehat {AHC} = \widehat {BAC} = {90^0},\widehat C\;chung\)
Do đó, \(\Delta ACH \backsim \Delta BCA(g.g)\)
Cho các mệnh đề sau. Chọn câu đúng .
(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
(II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
-
A.
(I) đúng, (II) sai
-
B.
(I) sai, (II) đúng
-
C.
(I) và (II) đều sai
-
D.
(I) và (II) đều đúng
Đáp án : A
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Vậy (I) đúng, (II) sai.
-
A.
\(\Delta IPQ \backsim \Delta IMN\)
-
B.
\(\Delta IPQ = \Delta IMN\)
-
C.
\(\Delta IPQ \backsim \Delta INM\)
-
D.
\(\Delta IPQ \backsim \Delta MNI\)
Đáp án : A
Do đó, \(\Delta IPQ \backsim \Delta IMN(g.g)\)
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\widehat B = \widehat F\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
Đáp án : B
Tam giác ABC và tam giác DEF có: \(\widehat {BAC} = \widehat {EDF} = {90^0},\widehat B = \widehat F\) nên \(\Delta ABC \backsim \Delta DFE(g.g)\)
Nếu \(\Delta MNP\) và \(\Delta DEF\) có \(\widehat{M}=\widehat{D}=90{}^\circ \) , \(\widehat{P}=50{}^\circ \) . Để \(\Delta MNP\,\backsim \,\Delta DEF\) thì cần thêm điều kiện
-
A.
\(\widehat{E}=50{}^\circ \) .
-
B.
\(\widehat{F}=60{}^\circ \) .
-
C.
\(\widehat{F}=40{}^\circ \) .
-
D.
\(\widehat{E}=40{}^\circ \)
Đáp án : D
\(\Delta MNP\) có \(\widehat{M}=90{}^\circ \) , \(\widehat{P}=50{}^\circ \) \(\Rightarrow \widehat{N}=40{}^\circ \) .
\(\Delta MNP\) và \(\Delta DEF\) có \(\widehat{M}=\widehat{D}\) (gt) cần thêm điều kiện \(\widehat{E}=40{}^\circ \) thì \(\Rightarrow \widehat{N}=\widehat{E}=40{}^\circ \)
Lúc này \(\Delta MNP\backsim \Delta DEF\) (g – g ).
Nếu \(\Delta DEF\) và \(\Delta SRK\) có \(\widehat{D}=70{}^\circ \) ; \(\widehat{E}=60{}^\circ \) ; \(\widehat{S}=70{}^\circ \) ; \(\widehat{K}=50{}^\circ \) thì
-
A.
\(\frac{DE}{SR}=\frac{DF}{SK}=\frac{EF}{RK}\) .
-
B.
\(\frac{DE}{SR}=\frac{DF}{RK}=\frac{EF}{SK}\) .
-
C.
\(\frac{DE}{SR}=\frac{DF}{SR}=\frac{EF}{RK}\) .
-
D.
\(\frac{DE}{RK}=\frac{DF}{SK}=\frac{EF}{SR}\)
Đáp án : A
\(\Delta DEF\) có \(\widehat{D}+\widehat{E}+\widehat{F}=180{}^\circ \Rightarrow 70{}^\circ +60{}^\circ +\widehat{F}=180{}^\circ \Rightarrow \widehat{F}=50{}^\circ \) .
\(\Delta DEF\) và \(\Delta SRK\) có \(\widehat{D}=\widehat{S}=70{}^\circ \) và \(\widehat{F}=\widehat{K}=50{}^\circ \) nên \(\Delta DEF\,\backsim \,\Delta SRK\) (g – g).
Suy ra \(\frac{DE}{SR}=\frac{DF}{SK}=\frac{EF}{RK}\) .
-
A.
\(\Delta ABC\,\backsim \Delta ABH\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta HAB\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta AHB\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta HBA\) .
Đáp án : D
\(\Delta ABC\) và \(\Delta HBA\) có góc \( \widehat{B}\) chung, \(\widehat{BAC}=\widehat{AHB}=90{}^\circ \) nên \(\Delta ABC\,\backsim \Delta HBA\) (g – g)
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\). Hệ thức nào sau đây đúng?
-
A.
\(AB = BC.BH\).
-
B.
\(A{C^2} = CH.BH\).
-
C.
\(A{H^2} = BH.CH\).
-
D.
\(AH = CH.BH\).
Đáp án : C

Xét \(\Delta HCA\) và \(\Delta HAB\) có:
\(\widehat {HAC} = \widehat B\) (Vì cùng phụ với \(\widehat {HAB}\) ); \(\widehat {CHA} = \widehat {AHB} = 90^\circ \)
nên \(\Delta HCA\,\, \backsim \,\Delta HAB\) (g – g ) \( \Rightarrow \frac{{AH}}{{BH}} = \frac{{CH}}{{AH}} \Leftrightarrow A{H^2} = BH.CH\).
Cho hình thang \(ABCD\) \(\left( {AB\,{\rm{//}}\,CD} \right)\), \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\). Khẳng định nào sau đây đúng
-
A.
\({\rm{\Delta }}OAB \backsim \,\Delta ODC\).
-
B.
\({\rm{\Delta }}CAB \backsim {\rm{\Delta }}CDA\).
-
C.
\({\rm{\Delta }}OAB \backsim {\rm{\Delta }}OCD\).
-
D.
\({\rm{\Delta }}OAD \backsim {\rm{\Delta }}OBC\).
Đáp án : C

Vì \(AB\,{\rm{//}}\,CD\) (gt) nên \(\widehat {ABO} = \widehat {ODC}\) (cặp góc so le trong) .
\({\rm{\Delta }}OAB\) và \(\,\Delta OCD\) có:
\(\widehat {ABO} = \widehat {ODC}\) (chứng minh trên); \(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
Nên \({\rm{\Delta }}OAB \backsim \,\Delta OCD\) (g – g ).
Cho hình thang \(ABCD\,\,\left( {AB\,{\rm{//}}\,CD} \right)\), \(\widehat {ADB} = \widehat {BCD}\), \(AB = 2\,{\rm{cm}}\), \(BD = \sqrt 5 \,{\rm{cm}}\). Độ dài đoạn thẳng \(CD\) là

-
A.
\(2\sqrt 5 \,{\rm{cm}}\).
-
B.
\(\sqrt 5 - 2\,{\rm{cm}}\).
-
C.
\(\frac{{\sqrt 5 }}{2}\,{\rm{cm}}\).
-
D.
\(2,5\,{\rm{cm}}\).
Đáp án : D
Vì \(AB\,{\rm{//}}\,CD \Rightarrow \widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong).
Xét \(\Delta \,ADB\) và \(\Delta \,BCD\) có:
\(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên); \(\widehat {ADB} = \widehat {BCD}\) (gt)
Nên \(\Delta \,ADB\, \backsim \Delta BCD\) (g – g ).
\( \Rightarrow \frac{{AB}}{{BD}} = \frac{{DB}}{{CD}} \Leftrightarrow \frac{2}{{\sqrt 5 }} = \frac{{\sqrt 5 }}{{CD}} \Leftrightarrow CD = \frac{{\sqrt 5 .\sqrt 5 }}{2} = \frac{5}{2} = 2,5\,\,\left( {{\rm{cm}}} \right)\).
Cho hình thang vuông \(ABCD\), \(\left( {\widehat A = \widehat D = 90^\circ } \right)\) có \(DB \bot BC\), \(AB = 4\,{\rm{cm}}\), \(CD = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(BD\) là
-
A.
\(8\,{\rm{cm}}\).
-
B.
\(12\,{\rm{cm}}\).
-
C.
\(9\,{\rm{cm}}\).
-
D.
\(6\,{\rm{cm}}\).
Đáp án : D
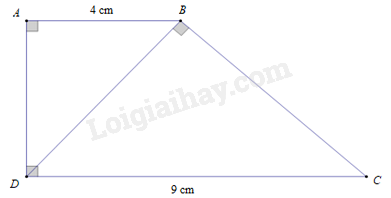
Ta có \(AB\,{\rm{//}}\,{\rm{CD}}\) ( vì cùng vuông góc với \(A{\rm{D}}\)).\( \Rightarrow \widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong)
Xét \(\Delta ABD\) và \(\Delta BDC\) có:
\(\widehat {BAD} = \widehat {DBC} = 90^\circ \); \(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên)
Nên \(\Delta \,ABD\,\, \backsim \,\Delta BDC\) (g – g) \( \Rightarrow \frac{{AB}}{{BD}} = \frac{{BD}}{{DC}} \Rightarrow B{D^2} = AB.DC = 4.9 = 36 \Rightarrow BD = 6\,\,\left( {{\rm{cm}}} \right)\).
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\) biết \(BH = 4\,{\rm{cm}}\), \(CH = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(AH\) là
-
A.
\(4,8\,{\rm{cm}}\).
-
B.
\(5\,{\rm{cm}}\).
-
C.
\(6\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
Đáp án : C
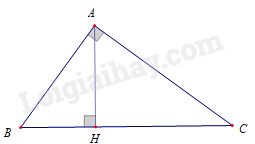
Xét \(\Delta HCA\) và \(\Delta HAB\) có :
\(\widehat {HAC} = \widehat B\) (Vì cùng phụ với \(\widehat {HAB}\)) ; \(\widehat {CHA} = \widehat {AHB} = 90^\circ \)
nên \(\Delta HCA\, \backsim \Delta HAB\) (g – g ) \( \Rightarrow \frac{{AH}}{{BH}} = \frac{{CH}}{{AH}} \Leftrightarrow A{H^2} = BH.CH\) .
\( \Leftrightarrow A{H^2} = 4.9 = 36 \Rightarrow AH = 6\,\left( {{\rm{cm}}} \right)\) .
Cho hình vẽ, biết \(\widehat {ACB} = \widehat {ABD}\), \(AB = 3\,{\rm{cm}}\), \(AC = 4,5\,{\rm{cm}}\). Độ dài đoạn thẳng \(AD\) là

-
A.
\(2\,{\rm{cm}}\).
-
B.
\(2,5\,{\rm{cm}}\).
-
C.
\(3\,{\rm{cm}}\).
-
D.
\(1,5\,{\rm{cm}}\).
Đáp án : A
Chứng minh \(\Delta ABC\, \backsim \Delta ADB\) (g– g ) \( \Rightarrow \frac{{AB}}{{AD}} = \frac{{AC}}{{AB}} \Leftrightarrow AD = \frac{{AB.AB}}{{AC}} = \frac{{3.3}}{{4,5}} = 2\,({\rm{cm)}}\)
Xét \(\Delta ABC\) và \(\Delta ADB\) có:
Góc \(A\) chung, \(\widehat {ACB} = \widehat {ABD}\) (gt)
Nên \(\Delta ABC\, \backsim \,\Delta ADB\) (g– g ) \( \Rightarrow \frac{{AB}}{{AD}} = \frac{{AC}}{{AB}} \Leftrightarrow AD = \frac{{AB.AB}}{{AC}} = \frac{{3.3}}{{4,5}} = 2\,({\rm{cm)}}\)
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 30\,{\rm{cm}}\), \(AC = 40\,{\rm{cm}}\). Kẻ đường cao \(AH\)\(\left( {H \in BC} \right)\). Độ dài đường cao \(AH\) là
-
A.
\(18\,{\rm{cm}}\).
-
B.
\(24\,{\rm{cm}}\).
-
C.
\(32\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
Đáp án : B
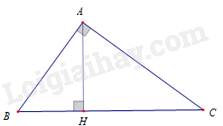
\(\Delta ABC\) vuông tại \(A\) nên \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{30}^2} + {{40}^2}} = \sqrt {2500} = 50\,\,\left( {{\rm{cm}}} \right)\).
\(\Delta ABC\) và \(\Delta HBA\) có góc \(B\) chung, \(\widehat {BAC} = \widehat {AHB} = 90^\circ \) nên \(\Delta ABC\,\, \backsim \,\Delta HBA\) (g – g ).
\( \Rightarrow \frac{{AC}}{{AH}} = \frac{{BC}}{{AB}} \Leftrightarrow \frac{{40}}{{AH}} = \frac{{50}}{{30}} \Leftrightarrow AH = \frac{{40.30}}{{50}} = 24\,\left( {{\rm{cm}}} \right)\).
\(\Delta ABC\) cân tại \(A\), hai đường cao \(AH\) và \(BK\), cho \(BC = 6\,{\rm{cm}}\), \(AB = 5\,{\rm{cm}}\). Độ dài đoạn thẳng \(BK\) là
-
A.
\(4,5\,{\rm{cm}}\).
-
B.
\(4,8\,{\rm{cm}}\).
-
C.
\(3\,{\rm{cm}}\).
-
D.
\(4\,{\rm{cm}}\).
Đáp án : B
Chứng minh \(\Delta AHC \backsim \Delta BKC\) ( g – g )\( \Rightarrow \frac{{AH}}{{BK}} = \frac{{CA}}{{CB}}\,\,\,\, \Leftrightarrow BK = \frac{{AH.CB}}{{CA}} = \frac{{4.6}}{5} = 4,8\left( {{\rm{cm}}} \right)\,\)
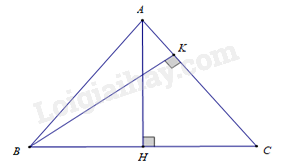
Ta có \(\Delta ABC\) cân tại \(A\) \( \Rightarrow AC = AB = 5\,\left( {{\rm{cm}}} \right)\).
Vì \(\Delta ABC\) cân tại \(A\) nên \(AH\) là đường cao đồng thời là đường trung tuyến ứng với cạnh \(BC\) \( \Rightarrow HB = HC = \frac{{BC}}{2} = \frac{6}{2} = 3\,\left( {{\rm{cm}}} \right)\).
Áp dụng định lí Pytago vào tam giác vuông \(ABH\) ta có:
\(A{H^2} = A{B^2} - H{B^2} = {5^2} - {3^2} = 16\) \( \Rightarrow AH = 4\,\left( {{\rm{cm}}} \right)\)
Xét \(\Delta AHC\) và \(\Delta BKC\) có: góc \(C\) chung; \(\widehat {AHC} = \widehat {BKC} = 90^\circ \).
Nên \(\Delta AHC \backsim \Delta BKC\) ( g – g )\( \Rightarrow \frac{{AH}}{{BK}} = \frac{{CA}}{{CB}}\,\,\,\, \Leftrightarrow BK = \frac{{AH.CB}}{{CA}} = \frac{{4.6}}{5} = 4,8\left( {{\rm{cm}}} \right)\,\).
\(\Delta ABC\) vuông tại \(A\) có \(\widehat B = 60^\circ \), \(BD\) là phân giác \(\widehat B\), \(AC = 18\,{\rm{cm}}\). Độ dài đoạn thẳng \(BD\) là
-
A.
\(12\,{\rm{cm}}\).
-
B.
\(10\,{\rm{cm}}\).
-
C.
\(9\,{\rm{cm}}\).
-
D.
\(8\,{\rm{cm}}\).
Đáp án : A
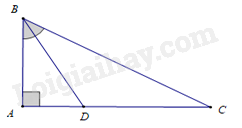
\(\Delta ABC\) có \(\widehat A = 90^\circ \) nên \(\widehat B + \widehat C = 90^\circ \Rightarrow \widehat {ACB} = 30^\circ \).
Vì \(BD\) là phân giác của \(\widehat B\) nên \(\widehat {ABD} = \widehat {DBC} = \frac{1}{2}\widehat {ABC} = 30^\circ \).
Xét \(\Delta ABC\) và \(\Delta ADB\) có: \(\widehat {ACB} = \widehat {ABD} = 30^\circ \); \(\widehat A\) chung
Nên \(\Delta ABC \backsim \Delta ADB\) ( g – g ) \( \Rightarrow \frac{{BC}}{{BD}} = \frac{{AC}}{{AB}} \Leftrightarrow BD = \frac{{AB.BC}}{{AC}}\).
Xét \(\Delta ABC\) có \(\widehat A = 90^\circ \), \(\widehat C = 30^\circ \) nên \(\Delta ABC\) là nửa tam giác đều \( \Rightarrow BC = 2AB\).
Áp dụng định lí Pytago vào \(\Delta ABC\) có:
\(B{C^2} = A{B^2} + A{C^2} \Leftrightarrow {\left( {2AB} \right)^2} = A{B^2} + {18^2} \Leftrightarrow 3A{B^2} = 324 \Leftrightarrow AB = \sqrt {108} \,{\rm{cm}}\).
\( \Rightarrow BC = 2\sqrt {108} \,{\rm{cm}}\). Từ đó \(BD = \frac{{AB.BC}}{{AC}} = \frac{{\sqrt {108} .2\sqrt {108} }}{{18}} = 12\,({\rm{cm)}}\).
-
A.
x = 15
-
B.
x = 16
-
C.
x = 7
-
D.
x = 8
Đáp án : A
Ta có \(\frac{{AB}}{{AC}} = \frac{6}{9} = \frac{2}{3},\frac{{AC}}{{CD}} = \frac{9}{{13,5}} = \frac{2}{3}\)
\( \Rightarrow \frac{{AB}}{{AC}} = \frac{{AC}}{{CD}} = \frac{2}{3}\)
Xét \(\Delta ABC\) và \(\Delta CAD\) có: \(\frac{{AB}}{{AC}} = \frac{{AC}}{{CD}}(cmt),\widehat {BAC} = \widehat {ACD}\) (so le trong, AB//CD )
\(\begin{array}{l} \Rightarrow \Delta ABC \backsim \Delta CAD(c - g - c)\\ \Rightarrow \frac{{AB}}{{AC}} = \frac{{CA}}{{CD}} = \frac{{BC}}{{AD}} = \frac{2}{3}\\ \Rightarrow \frac{{10}}{x} = \frac{2}{3} \Rightarrow x = \frac{{10.3}}{2} = 15\end{array}\)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}=\widehat{D}\) , \(\widehat{C}=\widehat{F}\) thì
-
A.
\(\Delta ABC\backsim \Delta DEF\) .
-
B.
\(\Delta CAB\backsim \Delta DEF\) .
-
C.
\(\Delta ABC\backsim \Delta DFE\) .
-
D.
\(\Delta CAB \backsim \Delta DFE\)
Đáp án : A
Xét \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}=\widehat{D}\) , \(\widehat{C}=\widehat{F}\) nên \(\Delta ABC\backsim \Delta DEF\) (g – g)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}={{70}^{\circ }}\) , \(\widehat{C}={{60}^{\circ }}\) , \(\widehat{E}={{50}^{\circ }}\) , \(\widehat{F}={{70}^{\circ }}\) thì
-
A.
\(\Delta ACB\,\,\backsim \,\,\Delta FED\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta FED\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta DEF\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta DFE\) .
Đáp án : B
\(\Delta ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}={{180}^{\circ }}\Rightarrow {{70}^{\circ }}+\widehat{B}+{{60}^{\circ }}={{180}^{\circ }}\Leftrightarrow \widehat{B}={{50}^{\circ }}\) .
\(\Delta ABC\) và \(\Delta FED\) có \(\widehat{A}=\widehat{F}=70{}^\circ \) , \(\widehat{B}=\widehat{E}=50{}^\circ \) nên \(\Delta ABC\,\backsim \,\Delta FED\) (g – g ).
Cho \(\Delta ABC\,\backsim \,\Delta {A}'{B}'{C}'\) (g – g ). Khẳng định nào sau đây đúng
-
A.
\(\widehat{A}=\widehat{{{B}'}}\) .
-
B.
\(AB={A}'{B}'\) .
-
C.
\(\frac{AB}{AC}=\frac{{A}'{B}'}{{A}'{C}'}\) .
-
D.
\(\frac{AB}{AC}=\frac{{A}'{C}'}{{A}'{B}'}\) .
Đáp án : B
\(\Delta ABC\,\backsim \,\Delta {A}'{B}'{C}'\Rightarrow \frac{AB}{AC}=\frac{{A}'{B}'}{{A}'{C}'}\)
-
A.
\(\Delta HIG\backsim \Delta DEF\) .
-
B.
\(\Delta IGH\backsim \Delta DEF\) .
-
C.
\(\Delta HIG\backsim \Delta DFE\) .
-
D.
\(\Delta HGI\backsim \Delta DEF\) .
Đáp án : A
\(\Delta HIG\) và \(\Delta DEF\) có \(\widehat{H}=\widehat{D}\) , \(\widehat{I}=\widehat{E}\) (gt) nên \(\Delta HIG\,\,\backsim \Delta DEF\) (g – g ).
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu
-
A.
ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
có hai cặp cạnh tương ứng bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Đáp án : B
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
Nếu \(\Delta ABC\) và \(\Delta MNP\) có \(\widehat{A}=\widehat{N}\) ; \(\widehat{B}=\widehat{M}\) thì
-
A.
\(\Delta ABC\backsim \,\Delta MNP\) .
-
B.
\(\Delta CAB\backsim \Delta NMP\) .
-
C.
\(\Delta ABC\backsim \Delta PMN\) .
-
D.
\(\Delta ABC\backsim \Delta NMP\) .
Đáp án : D
\(\Delta ABC\) và \(\Delta NMP\) có \(\widehat{A}=\widehat{N}\) , \(\widehat{B}=\widehat{M}\) nên \(\Delta ABC\backsim \Delta NMP\) (g – g ).